副溶血性弧菌温度-PH双因素预警模型的建立

李 涛,宁喜斌,安秀华,符姜燕

(上海海洋大学,上海 201306)

副溶血性弧菌温度-PH双因素预警模型的建立

李 涛,宁喜斌＊,安秀华,符姜燕

(上海海洋大学,上海 201306)

以副溶血性弧菌Vp BJ1.1997为研究对象,采用均匀设计实验方法,建立并验证了温度范围为 7～43℃,pH范围为 5.5～10.0的生长动力学模型。结果表明,所选一级模型的拟合效果优劣依次为 Logistic方程 ＞Gompertz方程 ＞Linear方程,以Logistic方程为一级模型计算生长参数;二级模型采用平方根模型进行拟合,得到模型相关系数 r为0.9739,最低生长温度为 11.7769℃,最低生长 pH为 7.38,经 F检验和偏差因子、准确因子验证,模型可接受。

副溶血性弧菌,双因素预测模型,均匀设计

1 材料与方法

1.1 材料与仪器

副溶血性弧菌Vp BJ1.1997 购于中国科学院普通微生物菌种保藏管理中心;胰蛋白胨大豆肉汤(TSB) 上海市疾病预防控制中心;TCBS培养基 上海康润生物科技有限公司。

低温生化培养箱 LRH-250CL(温度波动 ± 1.0℃) 上海一恒科学仪器有限公司;台式酸度计InoLab pH730 德国WT W仪器。

1.2 菌种活化

挑取 24h斜面培养的 Vp BJ1.1997一环,接种于10mL TSB液体培养基中,37℃培养 12h,备用。

1.3 菌体生长的测定

取制备好的菌悬液0.1mL接种于装有 10mL TSB液体培养基的试管中 (接种量为 103～105cfu/mL),将试管按设计的条件培养,每隔 1h取样测定,采用平板计数法计数。每组培养条件平行 2次。

1.4 实验方案设计

1.4.1 均匀实验设计因素水平表的选择 本实验温度范围为7～43℃,pH为5.5～10.0,因素水平表如表1所示。

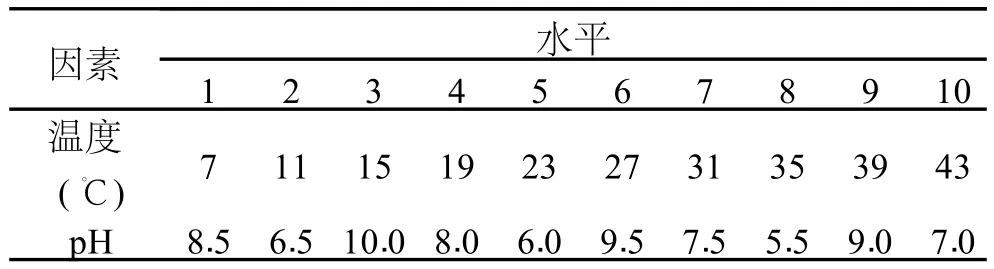
表1 因素水平表

1.4.2 均匀设计实验安排 采用 10因素 11水平的U11(1110)均匀设计表。根据均匀设计表的使用,2因素的U11(1110)均匀设计表选第 1、7列,其他列和第11行为空。

1.5 生长动力学模型的建立

1.5.1 一级模型 选定Linear方程、Gompertz模型及Logistic模型对实验数据进行拟合,三种模型生物学意义表达式如表 2[6]。

表2 三种模型生物学意义表达式

式中,N：微生物在时间 t时的生物量;N0：t=0时的初始菌数;A：t=+∞时的 lgN/N0,即当 N达到最大时所对应的值;U：生长速率;M：达到最大相对速率需要的时间。相关生长参数计算如下：

最大比生长速率

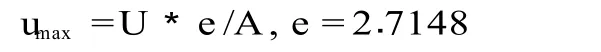
模型之间拟合效果的差异可通过比较相关系数r和残差平方和(RSS)来获知。r越接近于 1,RSS越小,说明模型的拟合效果越好。

1.5.2 二级模型 二级模型选用平方根模型,数学描述如下[7]：

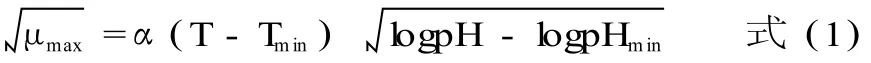
为避免当温度 T小于 Tmin或 pH小于 pHmin时,U为负值的情况,对模型修改如下：

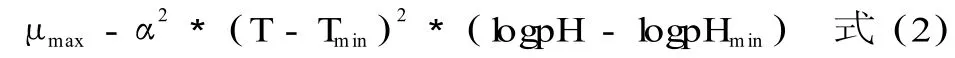
式中,μmax是最大比生长速率;Tmin是最低生长温度;α为系数。

1.5.3 模型验证 应用偏差因子 (bias factor)和准确因子 (accuracy factor)对模型预测效果进行验证和评价,计算公式如下：

2 结果与分析

2.1 不同温度-pH条件下Vp生长曲线的测定

根据VpBJ1.1997在不同温度-pH组合条件下的生长数据,绘制 Vp在不同培养条件下的生长曲线,并据生长趋势不同区分为图 1(A)和图 1(B)。

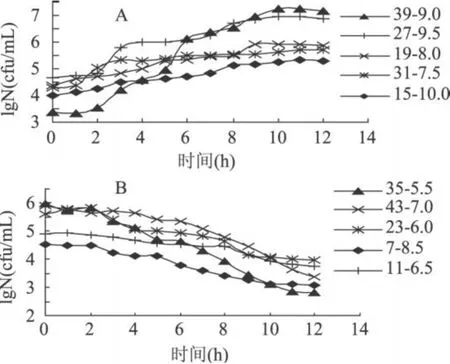
图 1 VpBJ1.1997不同组合培养条件下的生长曲线

从图 1(A)看出,在图中设定条件下培养 Vp呈正增长。温度-pH组合为 39-9.0时增长幅度最快,其次为 27-9.5,19-8.0、31-7.5和 15-10.0增长趋势较为缓和。此组条件比较发现,组合中温度均高于15,pH均高于 7.5。

从图 1(B)看出,在图中在设定条件下培养 Vp呈负增长。温度-pH组合为 35-5.5时下降幅度最大,其次为 43-7.0,再次为 23-6.0,11-6.5时下降幅度最小,下降趋势最为缓和。此组条件比较发现,除7-8.5组合条件外,其余各组合 pH均低于 7.0,而 7-8.5组合中温度值较Vp生长温度偏低。

2.2 一级模型的拟合

Linear方程多用于微生物在低温条件下生长曲线的拟合,Gompertz方程、Logistic方程为 S形曲线函数方程,在微生物生长动力学研究中较为常用。运用DPS数据处理系统,对各条件下Vp的生长曲线进行回归,得到部分统计分析结果,如表 3。

三种方程的拟合效果进行比较,10组实验数据全部通过 Logistic方程拟合所得的 r值最高,对应的RSS值最小;其次为 Gompertz方程拟合所得的 r值较高,对应的 RSS值较小;而通过 Linear方程拟合所得的 r值均在同组比较中最低,对应的RSS值最大。由此得出,Logistic方程在本实验中拟合效果优于Gompertz方程,为最好;Linear方程的拟合效果最差。对 Logistic方程拟合结果进一步做统计学验证并计算μmax,如表 4。

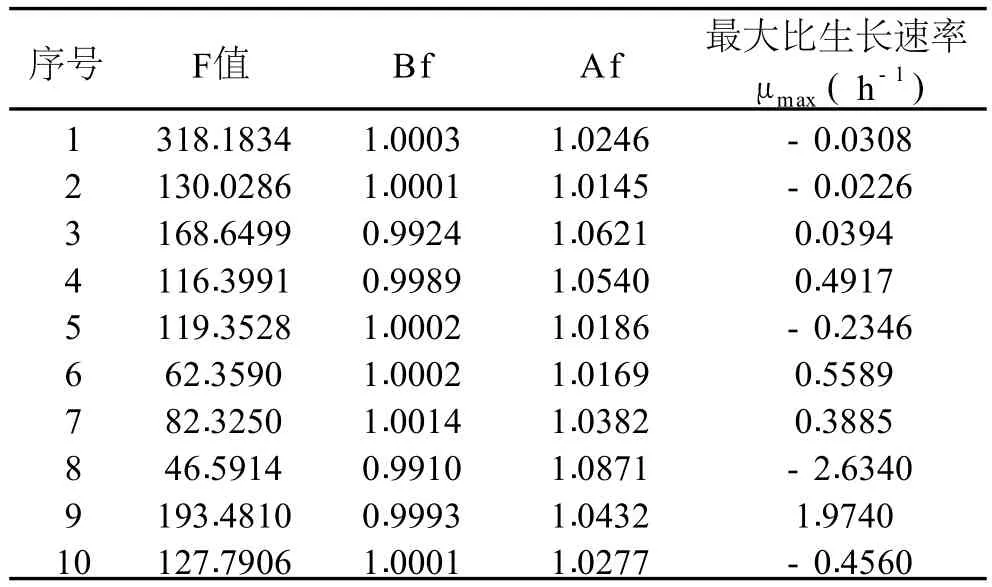
表 4 Logistic方程统计学验证及μmax计算结果表

表6 模型回归系数统计分析结果

从表 4中可看出,在显著性差异分析中,10组数据的 F值均大于 F0.01(2,10),即 P＜0.01,因此在α= 0.01水平上差异极显著,说明模型回归效果较好;计算得Bf最小值为 0.9910,最大值为 1.0014,均接近 1,说明模型预测效果较好;Af最小值为 1.0145,最大值为 1.0871,均接近 1,说明预测值与实测值的平均误差合理,模型可以接受。因此选定Logistic方程作为一级生长模型,进而计算μmax,得比生长速率最大培养条件组合为 39-9.0,μmax可达 1.9740h-1,生长速率最小组合为 35-5.5,μmax为-2.6340h-1,与图 1直接观察结果相符。

2.3 二级模型的拟合

据表 4中计算所得的生长速率,用平方根模型(2)进行拟合,建立二级模型。所得模型为：

μmax=0.18252＊ (T-11.7769)2＊ (logpH-0.8670)

模型相关系数 r=0.9739,其中α=0.1825,Tmin= 11.7769,logpHmin=0.8607,即 pH=7.3773。由模型表达式中得出,实验组 1、2、5、8、10为负值,其余为正值,与实测结果相符。值得注意的是,微生物在极限生长条件的生长速率难以准确测定,因此模型预测的最低生长温度可能不是该菌的实际最低生长温度。可观测的 Tmin值与 pHmin因选用不同菌株或使用不同培养基而有差异,但预测的 Tmin值与 pHmin是微生物的固有属性,不随培养基变化而变化[8]。二级模型的部分统计分析结果如表 5所示。

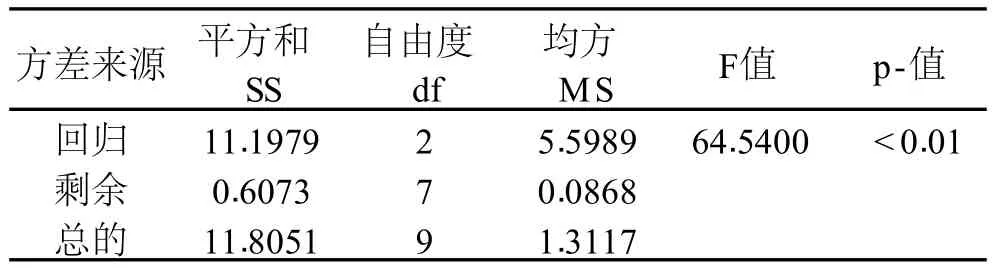
表5 模型统计分析结果

模型总体的显著性可以通过 F统计量进行假设实验。从模型的统计分析结果来看,模型 F＞F0.01(2,7),即 P＜0.01,因此在α=0.01水平上差异极显著,说明模型整体回归效果较好。对模型回归系数进行统计分析,如表 6所示。

从表中可看出,Tmin的 t值均大于 t0.05(7),回归系数达到显著水平;pH的 t值大于 t0.01(7),回归系数达到极显著水平,其对应最低生长 pH的 95%置信区间为 7.3773±1.0347。利用函数绘制平台 1.2版绘制模型三维曲面拟合图,如图 2所示。

图2 模型拟合图

2.4 模型验证

以 TSB培养基为基质,将Vp在任意 5组组合培养条件下培养,生长速率实测值和预测值进行比较分析,结果如表 7所示。

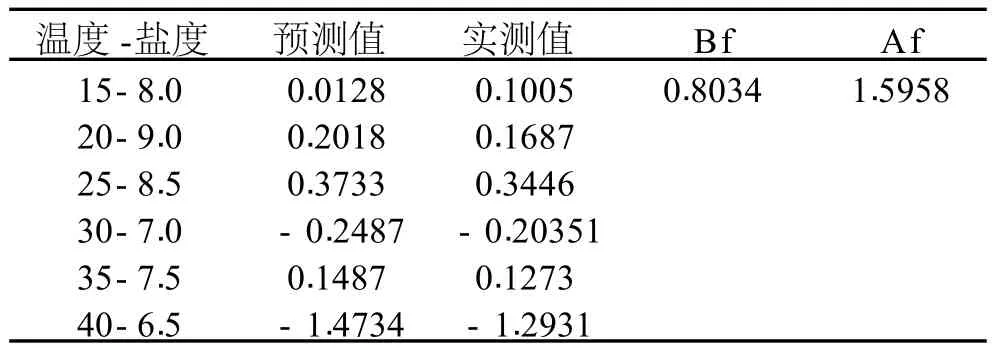
表7 培养基数据的统计学验证

利用Bf和Af对模型进行验证,Bf为 0.8034(n= 5),Af为 1.5958(n=5)。Bf小于 1表明生长速率预测值比实测值大,一般认为 Bf在 0.75～1.25之间,模型即可接受;Af等于 1表明预测值与实测值完全吻合,一般在 1.1～1.9之间均可接受[9]。该模型Bf和Af值均在合理范围内,说明模型可接受。

3 结论与讨论

3.1 利用DPS数据处理系统对不同温度-pH条件下 VpBJ1.1997的实验数据进行拟合,结果表明, Logistic模型比 Gompertz模型及线性模型能更好地拟合副溶血性弧菌的生长,在α=0.01水平上模型极显著。拟合结果表明,培养温度-pH组合为 39-9.0时,Vp比生长速率最大,组合为 35-5.5时,Vp比生长速率最小。

3.2 利用平方根模型对Vp进行最大比生长速率与温度-pH之间关系的拟合,得到Vp生长的二级双因素模型。预测得知,Vp的最低生长温度为11.7769℃,最低生长 pH为 7.3773。F检验表明模型在α=0.01显著,培养基数据Bf和Af验证值在可接受范围内,回归系数分析表明回归系数显著,说明此模型能较好描述Vp比生长速率与温度-pH之间的对应关系。

3.3 均匀设计由数学家方开泰和王元 1978年创立,与传统“正交设计”相比,均匀设计将实验点在高维空间内充分均匀分散,使数据具有更好的代表性,为揭示规律创造必要条件。均匀设计在多水平实验研究中有重要意义,在实验点均匀分散的同时可大大减少工作量,缩短实验周期,在医药、化工、食品及生物工程等领域都有应用。本文尝试将均匀设计方法引入到微生物生长预测模型的建立过程中,并得到较好的实验效果。但在微生物生长动力学研究中,大量数据的积累十分重要,均匀设计虽在水平数不变的条件下可减少实验次数,其精准性应进一步进行验证比对。

[1]刘秀梅,陈艳,等 .1992～2001年食源性疾病暴发资料分析——国家食源性疾病监测网[J].卫生研究,2004,33(6)：725-727.

[2]俞莺,宁喜斌 .对虾副溶血性弧菌的风险评估[J].现代食品科技,2006,23(5)：184-186.

[3]陈瑞英,鲁建章,苏意诚,等 .食品中副溶血性弧菌的危害分析、检测与预防控制[J].食品科学,2007,28(1)：341-346.

[4]王璐华,宁喜斌 .副溶血性弧菌生长预测模型的建立与应用探讨[J].华北农学报,2008,23(增刊)：263-267.

[5]杨振泉,焦新安 .副溶血性弧菌在低温贮藏过程中的失活动力学特征[J].食品科学,2008,29(7)：47-51.

[6]RatkowskyDA著,洪再吉等译 .非线性回归模型统一的实用方法[M].南京：南京大学出版社,1986：71-81.

[7]Adams M R,Little C L,Easter M C.Modeling the effect of pH,acidulant and temperature on the growth rate of yersinia enterocolitica[J].J ApplBacteriol,1991,71：65-71.

[8]MilesDW,Ross T,Olley J,et al.Development and evaluation of a predictive model for the effect of temperature and water activity on the growth rate of Vibrio parahaemolyticus[J].Food Microbiol,1997,38：133-142.

[9]Braun P,Sutherland JP.Predictive modeling of growth and enzyme production and activity by a cocktail of Pseudomonas spp., Shewanella putrefaciens andAcinetobacter sp[J].FoodMicrobiol, 2003,86：271-282.

Developm ent of predictive model for com bined effect of temperature and pH on the grow th ofVibrio parahaemolyticus

L I Tao,NING Xin-b in＊,AN Xiu-hua,FU Jiang-yan
(College of Food Science,ShanghaiOcean University,Shanghai 201306,China)

Based on the s tanda rd s tra in-Vib rio p a rahaem olyticus BJ1.1997,its g row th s ta tus which affec ted by temp e ra ture(7～43℃)and pH(5.5～10.0)was s tud ied w ith uniform des ign.Theresults showed tha t Log is tic equa tion was op t im a l in p r im a ry m ode ls,while Gomp e rtz equa tion was m ore adap tab le than Linea r,so g row th p a ram e te rs we re ca lcula ted from Log is tic equa tion.The seconda ry m ode lwas deve lop ed by squa re rootm ode ls.Its rva lue was0.9739,the lowes t g row th temp e ra ture was11.7769℃and the lowes t g row th pH was7.38.Through F tes t and eva lua tion by b ias fac tor and accuracy fac tor,the m ode l can exac tly desc ribe the re la tionship be tween the g row th ra te and com b ined effec t of temp e ra ture and pH.

Vib rio p a rahaem olyticus;doub le-fac tors p red ic tive m ode l;uniform des ign

TS201.3

A

1002-0306(2010)03-0091-04

副溶血性弧菌 (V ibrio parahaem olyticus,简称Vp)又称嗜盐菌,广泛分布于海湾、海岸线区域、盐湖及海产品中,温热地带较多,是沿海地区引起微生物性食物中毒的重要病原菌。国家食源性疾病监测网数据显示,沿海省份副溶血性弧菌引起的食物中毒已高居微生物性食物中毒的首位[1]。该菌在水产品中的天然带菌率较高,温暖季节在海虾中可高达90%[2],生长繁殖达一定量可引发人体病变,因此研究副溶血性弧菌在水产品中的生长动力学状况,建立预警机制,对于保证水产品安全性具有重要意义。影响副溶血性弧菌生长的因素很多,如温度、盐度、pH等。副溶血性弧菌在含盐 0.5%～8%的环境中生长,含盐量为 2%～4%生长最佳,无盐或高盐 (10%)不生长;在温度为 5～44℃范围内生长,以 30～35℃为最佳;适宜生长的 pH为 7.5～8.5,以 pH7.7为最佳, pH低于 6则生长不佳[3]。目前国内学者多进行单因素生长动力学研究,并主要以温度为对象,已建立了副溶血性弧菌的温度预测模型以及低温失活模型等[4-5],多因素协同作用模型的建立方法报道较少。本研究以温度-pH交互作用为对象进行研究,鉴于副溶血性弧菌所涉及单因素生存范围较宽、研究二因素交互作用时所取水平数较多而采用均匀设计,对副溶血性弧菌二级双因素模型的建立方法进行初步探讨。

2009-04-22 ＊通讯联系人

李涛(1985-),女,在读硕士,研究方向：食品安全与检测。

国家自然科学基金项目资助 (30771675);上海市教育委员会重点学科建设项目资助(J50704)。