大跨径多塔连跨悬索桥结构特性影响因素分析
郑小燕, 徐 岳
(1.长安大学旧桥检测与加固技术交通行业重点实验室,陕西 西安 710064;2.合肥工业大学交通运输工程学院,安徽 合肥 230009)
0 引 言
超大跨径的连续悬索桥(多塔连跨悬索桥)是桥梁实现超长和超大跨完美结合的最佳途径,各国学者、桥梁工程师们曾为跨海工程提出过众多的多塔悬索桥方案,比如为建设美国旧金山-奥克兰西海湾桥而提出的三塔四跨悬索桥方案、在意大利墨西哥海峡方案比选时提出的双主跨1 750 m的三塔四跨悬索桥方案。此外,直布罗陀海峡的规划中则有多个不同的多塔悬索桥方案;勃朗(Brown Beech B2)公司于1994年为第二英法海峡跨越工程提出了三塔四跨悬索桥方案;日本东京湾、津轻海峡、丰予海峡的跨越方案中均有多塔悬索桥;我国在琼州海峡、青岛海湾大桥、阳逻长江大桥、河南中原黄河公路大桥、南京长江四桥以及螺洲大桥等工程的方案设计中都曾提出过多塔悬索桥方案。
但目前大跨径多塔悬索桥少有实践,结构特性的详细研究还较为欠缺,更没有可供遵循的设计方法。基于性能设计方法是可以按照不同的设计标准,使所设计的工程结构在使用期间满足各种预定的性能目标要求,打破了当前单一化的结构设计方法,是未来结构设计的发展方向。基于性能的个性化设计思路,适合应用于大跨径多塔悬索桥的设计。
本文在回顾多塔悬索桥结构特性研究的基础上,对影响大跨径多塔悬索桥结构性能的设计参数进行分析,探讨各参数在设计中的重要程度,为建立多目标优化的设计方法奠定基础。
1 大跨径多塔悬索桥结构体系
多塔连跨悬索桥是以多塔支承的连续主缆,固定主缆首尾两端的锚碇和不一定完全连续的加劲梁构成的悬吊体系,如图1所示。
它省去了连续布置的双塔悬索桥的中央共用锚碇。不同于传统的双塔悬索桥,中间主塔在纵向只是一个通过鞍座支承主缆的竖向支点。

图1 多塔连跨悬索桥
2 多塔悬索桥结构特性研究回顾
目前关于多塔悬索桥的建设几乎没有成熟的经验,国外的研究仅局限在一些桥梁的方案研究阶段,而我国关于多塔悬索桥的研究多是围绕泰州长江公路大桥的设计和建设,针对三塔两主跨悬索桥而进行的。
2.1 多塔悬索桥静力特性研究
丹麦的Niels J.Gimsing[1]曾对拟定的2座千米主跨悬索桥(传统的三跨缆索与具有两相等主跨的四跨缆索体系)进行研究,比较加劲梁的竖向挠度和塔顶纵向位移。研究表明,四跨缆索体系的最大挠度比三跨缆索体系的大1倍多,而大挠度引起的中塔纵向位移达到7.5 m,将近三跨体系的4.7倍。可以看出,多塔连续悬索桥的关键问题是其整体刚度,20世纪60年代T.Fukuda曾研究过一四跨悬索桥(跨径布置400 m+1 150 m+1 150 m+400 m),发现中心三角形索塔可以给结构体系提供较好的刚度特性。Niels J.Gimsing将T.Fukuda的研究成果与旧金山-奥克兰西海湾桥方案之一的四跨悬索桥(跨径布置393 m+1 036 m+1 036 m+393 m)模型试验结构进行了对比。
两座桥跨径布置和荷载均相似,但T.Fukuda研究的体系最大挠度只有旧金山-奥克兰西海湾桥模型体系挠度的30%,清楚表明三角形桥塔对体系整体刚度的贡献[1]。
文献[2]研究了多跨悬索桥的刚度解决方案,从增加主梁或桥塔刚度和改变缆索系统2个方面进行了分析,认为三角形桥塔体系和双链缆索体系对大跨度多跨悬索桥非常合适。
文献[3]也在分析日本未来的跨海项目实施中应注意的问题时,指出多跨悬索桥的关键问题是中间塔的设计,并给出中间塔不能设计成刚性结构,而只能是柔性塔的原则。
文献[4]研究了一座两主跨径为2 000 m的四跨悬索桥的变形特征,重点分析中间塔刚度、主缆垂度以及空间缆索系统对多塔悬索桥受力的影响。研究显示,中塔弯曲刚度愈大和垂跨比愈小,活载作用产生的主梁竖向挠度和塔顶纵向位移就愈小。文献[4]还引入“缆索弹簧刚度”的概念,认为四跨悬索桥加劲梁在活载作用下的较低刚度是因为主跨主缆的弹性刚度系数只有边跨的1/6造成的。
文献[5,6]也对大跨径多塔悬索桥的静动力特性进行了参数研究。
基于泰州长江公路大桥的设计,文献[7,8]着眼于主缆抗滑移安全系数、加劲梁竖向最大活载挠度以及中塔塔顶位移等指标,分析了主缆矢跨比、加劲梁高度、中主塔高度以及结构约束条件变化对结构整体性能的影响,得到较大的垂跨比对结构受力较为有利的结论。当垂跨比增大时,加劲梁的最大活载挠度、桥塔竖向力及主缆恒活载水平力均有减小趋势。另外还有一些关于中塔设计方面的研究。
2.2 多塔悬索桥动力特性研究
2.2.1 振动特性
相比于静力性能方面的研究,目前关于多塔悬索桥动力性能的相关文献较少。文献[4]研究了垂跨比、中间桥塔的弯曲弹簧系数变化时四跨悬索桥一阶对称弯曲振型和一阶对称扭转振型的频率变化情况,认为中塔弹簧系数愈大,弯曲固有频率愈大;当中塔刚度小于某一特定值时,弯曲固有频率随垂跨比增大而减小,而当中塔刚度大于这一特定值时,弯曲固有频率与垂跨比的关系呈现相反趋势;垂跨比一定时对称扭转振型频率随中塔扭转刚度增加而增加,但当中塔扭转刚度超过某一定值时,增加趋势不再显著;保持中塔扭转刚度不变时,增大垂跨比,扭转固有频率随之增大。文献[3,6]也有类似的结论。
根据文献[5],当中间桥塔具有足够的刚度时,多跨悬索桥的动力特性(竖向挠曲与扭曲振动频率)不随跨数的多少而变化。根据文献[6]的结论,增加桥塔个数,多塔悬索桥的一阶反对称竖弯和侧弯频率都呈现增减交替的趋势,其中侧弯频率的摆动幅度较大;一阶正对称竖弯和侧弯频率呈现减增交替趋势,竖弯频率摆幅较大;一阶反对称扭转频率逐渐减小,但减幅较小。
可以看出,中塔刚度和垂跨比是影响多跨悬索桥自振频率的主要因素,而对于其它因素如主跨跨径、边中跨比、主梁约束方式等对多塔悬索桥自振频率的影响,研究较少,还不能获得相印证的结论。
2.2.2 抗风性能
多塔悬索桥方案的提出往往关乎较大距离的跨海工程,这种情况的风荷载作用下结构的稳定性尤为重要,但由于目前多塔悬索桥的研究尚处在方案阶段,关于其抗风性能的研究还非常少,而临界颤振风速的计算均以Selberg公式为依据。文献[4]的研究表明垂跨比一定时,临界风速随中塔扭转刚度的增加而增加。
国内关于多塔悬索桥抗风问题的研究也均集中于泰州长江公路大桥的原型,文献[9]将泰州大桥与相同主跨双塔悬索桥的动力特性、空气静力和动力稳定性进行了对比分析,发现由于中桥塔缺乏有效的锚固作用,三塔悬索桥自振频率和空气动力失稳临界风速明显比双塔悬索桥的低,而其静风稳定性要比双塔悬索桥好,这缘于2个主跨变形的相互制约作用。文献[10]则建立有限元分析模型,研究了三塔悬索桥非线性静风稳定性,指出大跨径三塔悬索桥静风失稳形态为空间弯扭耦合失稳,升力和扭矩是影响结构失稳的关键分力。文献[8]的研究说明较大的垂跨比对结构抗风较为有利,当垂跨比增大时,颤振临界风速提高。
文献[11]根据颤振稳定性和涡激共振阶段模型试验结果,认为加劲梁一阶反对称扭转模态为颤振的主要参于者,一阶反对称竖弯和一阶正对称竖弯也明显参于其中。
2.2.3 抗震性能
关于多塔悬索桥抗震性能的研究均以泰州长江大桥的三塔悬索桥为背景,文献[12]采用有限元分析的方法对其进行动力特性和地震反应分析,指出抗震设计中应重视的主塔截面位置。此外,该研究发现弹性索虽然对中塔内力反应影响不大,但可以减小边塔弯矩、主梁梁端位移以及主梁与次边跨间相对位移,对结构抗震有利;高阶振型对大跨度三塔悬索桥内力反应影响很大,尤其是对主塔的反应影响。
文献[13]详细分析了中塔的刚度、主缆的垂度、塔顶处主缆的间距、加劲梁的高度以及约束条件改变下,三塔悬索桥抗震性能。文献[13]的结果显示减小中塔的纵向刚度和增大中塔塔梁处的纵向约束刚度对抗震有益;而增大主梁高度、改变矢跨比和改变塔顶处主缆的间距,对中塔的纵向地震响应值影响不大;另外设置中央扣,对悬索桥抗震也是有益的。
3 设计参数影响趋势分析
多塔悬索桥结构性能的研究基本上是基于某一桥梁方案进行的,一般性的研究还比较缺乏,但对认识其结构行为已具有较大帮助。大跨径多塔悬索桥整体刚度较传统悬索桥有较大降低,而且力学行为有较大差距。在主跨跨径相等的情况下,多塔悬索桥的中跨跨中挠度比两塔悬索桥大很多,中间桥塔的塔顶水平位移、塔底的正负弯矩也有显著的增大,而边跨的挠度以及边塔的位移却变化不大。实际上,虽然多塔悬索桥中间主塔与双塔悬索桥主塔具有基本相似的结构行为,但存在量上的较大差别(等主跨条件下,三塔悬索桥的中塔塔顶位移与塔底弯矩是双塔悬索桥的近9.6倍[5]),发展成为质的不同。悬索桥在非对称活载作用下,主塔发生一定的变形以协调两侧主缆的不平衡力。对大跨径多塔悬索桥,如果中塔刚度较小,则主缆不平衡水平力较小,塔身所承受弯矩也较小,但桥梁变形较大;如果中塔刚度很大而不可弯曲变形,那主缆的不平衡水平力就只能转移由中塔塔顶鞍座承担,这时鞍槽与主缆间摩擦阻力不足的问题就体现出来。
将已有关于三塔悬索桥结构参数变化对结构特性影响的研究成果归纳,见表1所列。
由表1可以看出,对于结构性能的不同表现,各设计参数的影响相互耦合;总体表现为中塔纵向刚度是影响桥梁整体性能的关键控制因素,主缆垂跨比也对结构性能具有较大影响,边、主跨比,主梁刚度以及主梁支承形式对结构整体性能影响敏感性稍弱。

表1 三塔悬索桥结构参数影响分析
4 基于层次分析法的影响因素分析
由于各设计参数对大跨径多塔悬索桥结构性能的耦合影响作用,设计过程中选择参数的难度较大,数值分析工作量大。为减小设计方案选择阶段的仿真工作量,使用层次分析法对各影响因素进行敏感性分析,确定设计参数选择次序,提高方案设计效率。
4.1 层次分析法基本原理
层析分析法(AHP)是由美国运筹学家T.L.Saaty于1980年提出的解决复杂、多准则决策问题的处理方法,其基本原理是排序。该方法首先将决策问题看作受多因素影响的系统,进而按照各因素之间的隶属关系建立层次分析模型,由决策者对各因素进行两两重要性比较(构造判断矩阵),再利用数学方法,对各因素进行排序[14]。
构造判断矩阵使用T.L.Saaty提出的1~9的评判标度系统,各因素重要性权值可利用AHP提供的幂法、特征方根法和积法中的任一种方法(这里采用特征方根法)。特征方根法计算权重,主要是求解判断矩阵(用 A表示)的特征值问题,即

4.2 构建决策分析模型
根据各因素对结构性能的影响情况,建立设计参数选择决策分析模型,如图2所示。
本次分析的总目标是获得大跨径多塔悬索桥适宜结构,即目标层 A;准则层层次B是大跨径多塔悬索桥结构性能的体现;指标层C、D中的元素是影响各种性能指标的因素。

图2 大跨径多塔悬索桥结构性能影响因素决策分析模型
4.3 建立各层次判断矩阵群及一致性检验
使用1~9的评判标度系统,根据大跨径多塔悬索桥结构性能研究成果,分别对每一层次元素对相邻上一层元素的相对重要性进行专家评分,得到各级判断矩阵群。各因素的两两重要性判断评分主要依据文献[5-13]对我国在建大跨径三塔悬索桥的定量研究成果。
(1)第1层评估因素集权重系数计算及一致性检验。多塔悬索桥适宜结构A={静力性能,动力性能}=}。
准则层各因素对目标层重要性判断矩阵A-B见表2所列。
(2)第2层评估因素集权重系数计算及一致性检验。各指标对静力性能及动力性能影响重要性比较判断矩阵见表3、表4所列。
(3)第3层评估因素集权重系数计算及一致性检验。D层指标集对C层指标的影响重要性判断矩阵,见表5~表12所列。

表2 A-B判断矩阵

表3 B1-C判断矩阵

表4 B2-C判断矩阵

表5 C1-D判断矩阵
注:λmax=5.18,一致性检验指标CI=0.04,一致性检验比率CR=0.04<0.1。
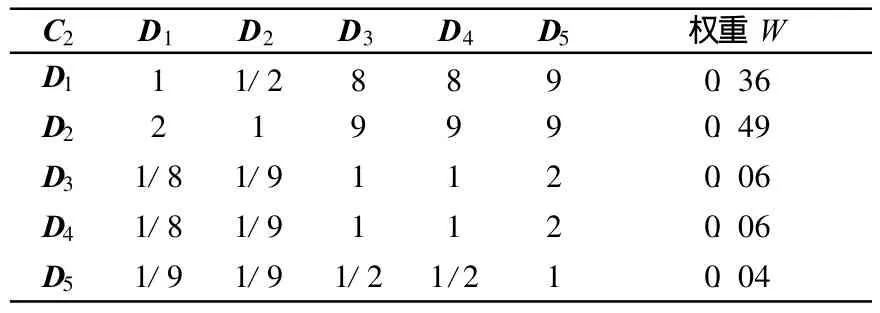
表6 C2-D判断矩阵

表7 C3-D判断矩阵

表8 C4-D判断矩阵

表9 C5-D判断矩阵

表10 C6-D判断矩阵

表11 C7-D判断矩阵
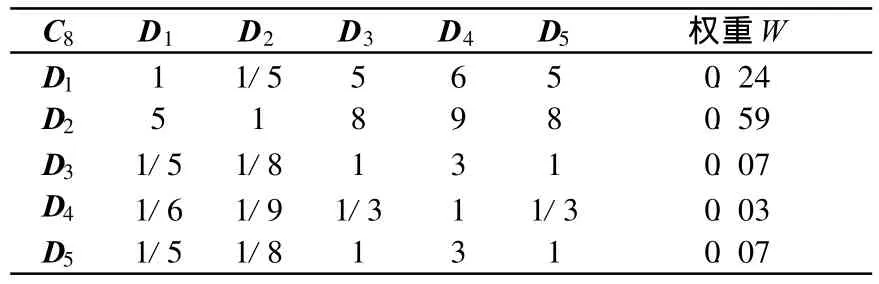
表12 C8-D判断矩阵
4.4 层次总排序及一致性检验
为了得到指标层C、D中的各元素相对于总目标层A的相对重要性权重值,需要进行层次总排序,最后进行一致性检验,确定计算结果的一致性。层次总排序和一致性检验结果见表13、表14所列。
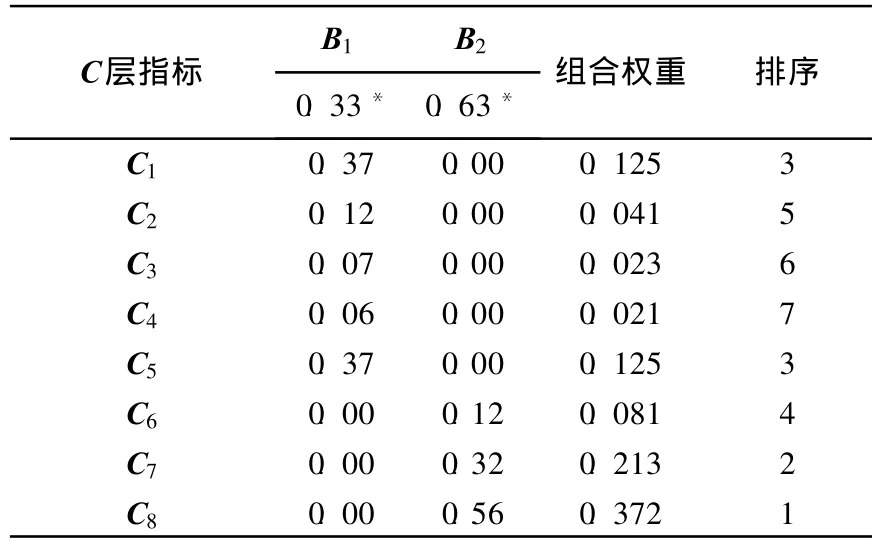
表13 C层指标对目标A的相对重要性排序及一致性检验
由表14组合权重系数可以看出,中塔刚度及主缆垂跨比2个参数对获得适宜结构最为重要,与前文分析结果一致,故所计算各参数权重指标可以作为设计参数选取时的参考。
虽然主缆垂跨比、中塔刚度等设计参数对大跨径多塔悬索桥结构体系的影响规律还需要进一步明确,但现有的研究基本可以表明各参数对结构性能影响的重要程度。
使用层次分析法,考虑结构的静、动力性能表现,对各设计参数的重要性进行了排序,依次为中塔纵向刚度,主缆垂跨比,加劲梁支承形式,边、主跨比和主梁刚度,这与多塔悬索桥一贯的研究成果相一致,可以作为设计方案阶段参数选择次序的参考。

表14 D层指标对目标A的相对重要性排序及一致性检验
[1] Gimsing N J.Cable supported bridges[M].2 nd ed.Chichester:John Wiley,1997:178-190.
[2] 陈艾荣,陈文明.多跨悬索桥的性能[C]//中国公路学会桥梁和结构学会2001桥梁学术研讨会论文集.北京:人民交通出版社,2001:561-566.
[3] 金增洪.21世纪日本的超长桥梁[J].中外公路,2001,21(6):1-5.
[4] Yoshida O,Okuda M,Moriya T.Structural characteristics and applicability of four-span suspension bridge[J].Journal of Bridge Engineering,ASCE,2004,(9/10):453-463.
[5] 王 萍.多塔连续体系悬索桥静动力特性的研究[D].成都:西南交通大学土木工程学院,2007.
[6] 朱本瑾.多塔悬索桥的结构体系研究[D].上海:同济大学土木工程学院,2007.
[7] 陈 策,钟建驰.三塔悬索桥关键设计参数对其结构行为的影响[J].世界桥梁,2008,(2):10-12,22.
[8] 陈 策,钟建驰.三塔悬索桥垂跨比变化对结构静动力特性的影响[J].桥梁建设,2008,(6):12-14,17.
[9] 张新军.三塔悬索桥的抗风稳定性分析[C].第十四届全国工程设计计算机应用学术会议论文集.杭州:浙江大学出版社,2008:69-74.
[10] 彭小刚,张文明,王 涛.大跨度三塔悬索桥非线性静风稳定分析[J].山东建筑大学学报,2008,23(5):435-437,470.
[11] 陈 策.大跨径三塔悬索桥抗风性能分析[J].铁道标准设计,2008,(2):31-33.
[12] 邓育林,彭天波,李建中,等.大跨度三塔悬索桥动力特性及抗震性能研究[J].振动与冲击,2008,27(9):105-110.
[13] 何友娣,李龙安,屈爱萍.三塔悬索桥的抗震性能研究[J].工程抗震与加固改造,2008,30(3):69-72.
[14] 王莲芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.

