基于倒立摆系统的自控原理实验设计*

张 伟 王亚维 洪 权 苗高亮

河南理工大学 河南焦作 454000

基于倒立摆系统的自控原理实验设计*

张 伟 王亚维 洪 权 苗高亮

河南理工大学 河南焦作 454000

自动控制原理是电气信息类学生的一门重要专业课，本文设计了基于倒立摆系统的自控原理辅助教学实验，使理论与实践相结合，有利于学生理解控制理论中的一些重要概念，了解实际系统的控制设计过程。同时可拓展学生的知识面，培养学生科研能力和创新思维能力。实践证明倒立摆教学实验具有很好的辅助教学效果，适于推广到一般二类本科院校的自控原理教学中。

倒立摆；自控原理；实验设计；MATLAB

自动控制原理是电气信息类学生的一门重要专业课，理论内容多且概念抽象，学生涉及实际系统的理论知识运用较少，使得学生学习兴趣不高，影响学习效果。倒立摆系统具有结构简单、直观性和趣味性等优点，且在理论上涉及了控制理论中的很多关键问题，其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途，因而成为控制理论教学和科研中不可多得的典型模型。

本文设计了基于倒立摆系统的自控原理辅助教学实验，以提高自控原理课程的教学效果。根据二类本科院校的学生特点，确定以直线一级倒立摆的稳定控制为目标，进行实验环节设计，具体阐述了对倒立摆系统的建模，传统PID控制器设计和基于现代控制理论的LQR控制器的设计、调试和仿真的整个过程。通过实验使学生能理论联系实际的理解和解决相关控制问题，实际教学验证了其良好的教学效果。

一、实验准备

1.以兴趣为内驱力，激发学生的学习动力

倒立摆系统由计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分组成一个闭环系统。利用倒立摆实际装置直观性、趣味性的特点激发学生学习兴趣，并通过讲明倒立摆系统的研究意义，引导学生进行主动学习。只有学生对实验产生兴趣，才会以积极的态度准备和开展实验，并愿意积极思考。本环节需让学生感受实际系统与理论所讨论的区别，控制环节与机械部分、信号采集和处理部分以及执行机构间的联系。

引入控制系统设计中广泛使用的MATLAB软件，介绍系统仿真的意义，进行简单的说明，包括实验中用到的语句（如验证系统的稳定性）及实验中涉及到的simulink工具箱中相关模块的使用。由于MATLAB软件可读性强，学生一般不仅不会感觉难，反而会有很大的学习热情。同时需提醒同学科学研究工作注重基础，但更侧重于创新问题的提出。

2.实验设计

根据二类本科学生的实际情况，以直线一级倒立摆系统的稳定控制为目标，按照一般的系统设计步骤（系统建模，模型仿真，控制器设计，系统仿真，实验验证）进行实验设计。实验环节包括建立倒立摆系统的数学模型；设计系统的PID控制器和LQR控制器，确定实验方案；通过MATLAB/simulink进行控制系统的仿真研究；有能力的同学，可进一步探讨控制方法对实物倒立摆的控制效果。需注意在实验前需给予学生理论到实际过渡所需的资料收集和思考时间。

二、建立倒立摆系统的数学模型

要进行倒立摆系统的控制研究，首先要对系统建立数学模型，这是设计控制器和进行仿真的基础。传统控制方法需建立倒立摆系统的线性化传函模型，现代控制方法较多地使用系统的状态方程表示。常见的数学建模方法是刚体动力学原理建模法。物理模型如图1所示。根据刚体动力学原理分析可得出如下公式：

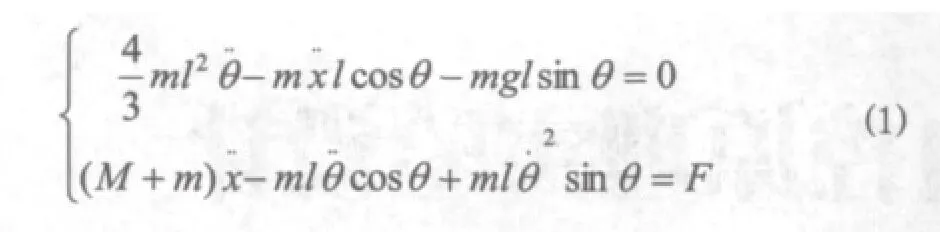
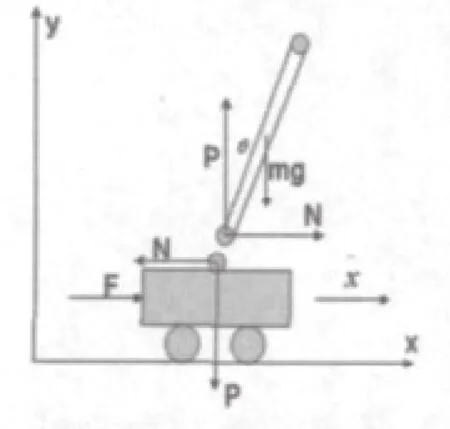
图1 直线一级倒立摆的物理模型

为分析方便，假设摆杆和小车均为刚体，摆杆匀质；忽略一切摩擦，小车与摆杆间可灵活的在-π/2到π/2间转动。

其中：M为小车质量；m为摆杆质量；l为摆杆长度；小车位置x；Q摆杆与垂线的夹角；小车水平受力F。到此就建立好了系统的数学模型

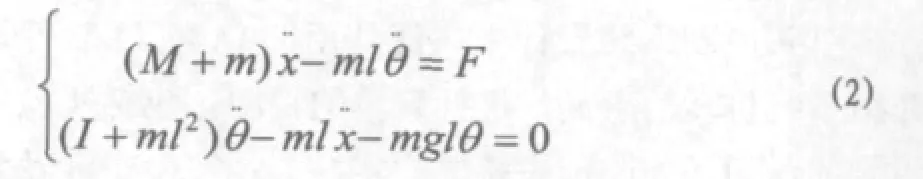
给定倒立摆系统的参数：

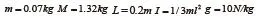
根据(2)，得到系统的传递函数：

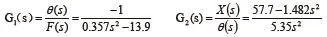
由数学模型可推导出系统的状态方程：

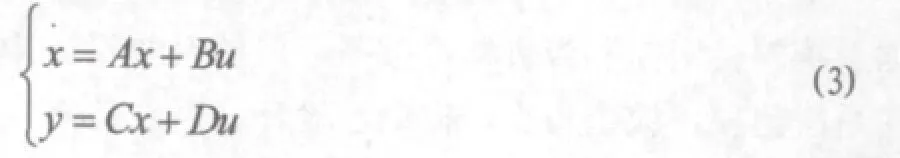
此环节需让学生明确建立系统模型并进行线性化处理的原因，工程的近似处理思想和了解常用的建模方法，并明确所讨论倒立摆的输入输出变量。

三、倒立摆PID控制器的设计

1.PID控制器

在经典控制理论中，PID控制是简单而有效的控制方法，现仍在工业控制中广泛应用。学生应明确PID控制器原理，在得到的系统数模型基础上，完成PID控制器的设计和仿真任务，实现倒立摆系统的稳定控制。要求（1）通过调节比例、积分、微分系数总结其对系统的作用，并与理论结果进行对比；(2)对倒立摆系统的控制效果用性能指标进行衡量，如上升时间、超调量、调整时间、稳态特性、动态特性等进行描述；（3）PID参数在调试过程中的遇到的问题及思考解决途径。图2是学生建立的双闭环PID控制器的仿真模型。图3为对应的仿真曲线。

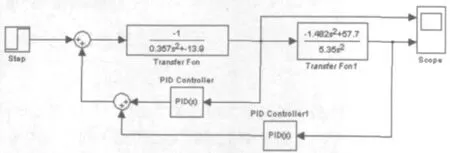
图2 simulink建立的双闭环PID仿真模型

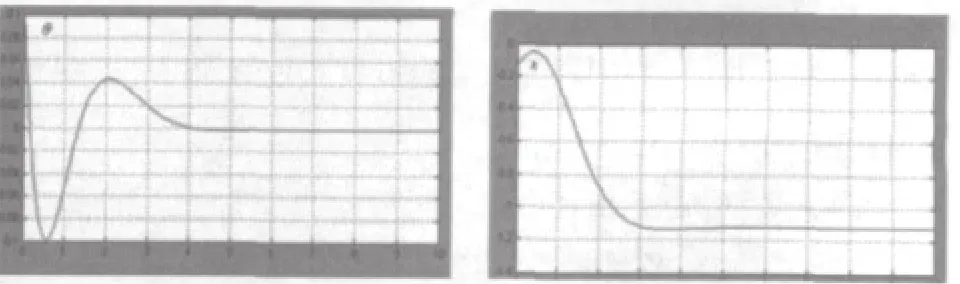
图3 PID控制器的输出量变化曲线

实际中由于PID参数调整经验因素成分大，若想实现倒立摆的稳定控制，需多次参数调整，部分同学会提出PID参数不易整定的问题。故引导学生考虑利用自控原理中极点配置法进行参数的初值设定，但请同学思考两者的结合点和实现途径。

2.极点配置法用于PID参数整定

极点配置法是自控原理中常用的方法。配置闭环极点的条件是受控系统可控且需将极点配置在左半复平面。首先利用得到的系统状态方程，进行条件判定。由MATLAB语句R=rank(ctrb(A,B))可验证系统满足可控性的条件，由MATLAB语句K=place（A,B,P）配置系统极点P=[-1+i;-1-i;-2+i;-2-i]，得K=[-26.4322 -4.0521 -1.2377 -1.8201]。分别设置为内外环PD整定参数为KP1=26.4322，KD1=4.0521，KP2=1.2377，KD3=1.8201，在此基础上微调参数，可得到PID最后整定参数，减少整定时间。请同学体会提出问题到解决问题的思维过程，并讨论配置的极点与系统响应之间的关系。

四、倒立摆LQR控制器的设计

线性二次型最优控制（LQR）是现代控制理论的重要组成部分，其理论依据是极小值原理，求解出的最优控制规律为状态变量的线性反馈，工程上容易实现，因许多控制问题又可概括为线性二次型最优控制问题，所以实际应用广泛。

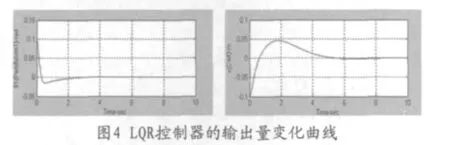
基于状态方程的各个参数，设定初始状态x0、Q和 R的取值，x0=[0.1;0;-0.1;0]，Q取单位阵，R取1，Q=diag(1000 1 10 1)时仿真曲线如图4所示，比传统PID控制效果好。由自控原理课程中涉及现代控制理论部分不多，此部分可做为有能力同学的知识扩充。并可在进一步进行实物倒立摆的实验验证工作，检验实际对象的控制效果。

五、结束语

本文以直线一级倒立摆系统为研究对象，设计了基于MATLAB的倒立摆系统实验，包括系统的建模环节、PID控制器设计和仿真环节、PID参数整定环节和LQR控制器设计仿真环节，理论与实际进行结合，较完整的体现了实际系统的设计过程。同时对提高自动控制原理教学效果也具有积极的作用。目前，所设计实验已用于本校电类自控原理课程的辅助教学中，取得了良好的教学效果。在此感谢学校大学生科研训练计划（SRTP）的资助。

[1]胡寿松.自动控制原理(第五版)[M].北京：科学出版社,2007

[2]俞立.现代控制理论[M].北京：清华大学出版社,2007

[3]徐国林，杨世勇.单级倒立摆系统的仿真研究[J].四川大学学报(自然科学版),2007，44:1013～1016

[4]李东,陈强，孙振国，等.倒立摆教学实验系统的设计与应用[J].实验技术与管理,2006，23:100～102

[5]薛定宇,控制系统计算机辅助设计—MATLAB语言与应用（第2版）[M].北京：清华大学出版社,2006

Experiment design of automatic control principle based on inverted pendulum system

Zhang Wei, Wang Yawei, Hong Quan, Miao Gaoliang
Henna polytechnic university, Jiaozuo,454000, China

The automatic control principle is an important course to the students of electrical information profession. The teaching experiments based on inverted pendulum system were designed as course’s assist study. That can help students understand some of the important concepts in the course and acknowledge the actual system’s control design process by combining theory with practice. Teaching experiments can also expand the students’ knowledge and culture their research capabilities and innovative thinking. In practice the inverted pendulum experiments are proved to have a good teaching aid effect, suitable for promotion to general high schools.

inverted pendulum; automatic control principle; experimental design; MATLAB

2010-04-10

张伟，硕士，讲师。

*本文系河南理工大学大学生科研训练计划SRTP：项目编号08-3-134。