随机利率下寿险定价风险的VAR分析

刘家军，黄少杰

(广东商学院数学与计算科学学院，广东广州510320)

随机利率下寿险定价风险的VAR分析

刘家军，黄少杰

(广东商学院数学与计算科学学院，广东广州510320)

在随机利率下对寿险定价的利率风险进行分析.通过对随机利率模型进行参数估计和假设检验，选择CIR模型为产生模拟利率的基础，推导出基于随机利率的定期寿险毛保费表达式，结合加拿大资产负债方法为产品定价，并利用在险价值（VAR）度量定价的利率风险.

CKLS模型；VAR；人寿保险；随机利率；加拿大资产负债方法

0 引言

利率风险是保险公司主要的风险因素，传统的保单在对寿险产品定价时是以一个预定利率进行贴现.但是市场利率不是固定不变的，当市场利率低于预定利率时，保险基金的收益水平下降，会给保险公司带来损失.当市场利率高于预定利率时，投保人又有可能会为获得更高的收益而退保，同样会给保险公司带来偿付能力方面的风险.为了有效规避利率波动给保险公司带来的风险，有必要使用随机利率对保险产品进行利率风险的分析.

1 随机利率模型实证分析

1.1 思路概述

由于使用预定利率定价缺乏灵活性，一些学者尝试利用随机利率对寿险产品进行定价.1976年，Boyel[1]考虑了寿险与年金中死亡率与利率均为随机的情况，即所谓的“双随机性”.吴金文和杨静平[2]针对随机利率寿险模型，考虑一保单组平均给付额的性质，但是利率的不确定性仍然存在；赵静宇、郭士杰、罗传光[3]把Vasicek模型引入到寿险产品定价研究中，推导出在随机利率下毛保费的分布，讨论了以毛保费均值和中位数定价的合理性.

大部分文献是通过随机利率为保险产品定价.当前，我国的保险监督机构对保险定价的预定利率有十分严格的规定，导致随机利率定价无法直接应用在实务中.不过，可以根据预定利率定出的价格，在随机利率的环境下，分析损失的可能.本文把银行业的风险管理工具VAR系统引入到寿险定价中，分析传统方法定出的价格所面临的利率风险，用实例说明VAR在化解利率风险方面的作用，并实证了加拿大资产负债方法[4]在定价方面的应用.

1.2 利率期限结构的单因子模型

目前国际上对随机利率的研究主要是4个重要的利率期限结构的单因子模型：Merton模型、Vasicek模型、CIR模型和CKLS模型.CKLS模型是其中最一般的模型[5]，其它模型都是CKLS模型的特例.CKLS模型假设利率服从随机过程rt，rt满足：

其中rt是利率，Wt是布朗运动，α=kθ，β=-k，k是均值回归的速率，k＞0，θ是利率均值，σ是利率的标准差，θ和σ为常数.θ表示rt的长期水平，它又是一临界值，当rt=θ时，漂移项k（θ-rt）·d t为零，当rt＞θ时，漂移项为负，这样rt有向下运动的趋势，当rt＜θ时，rt有向上运动的趋势，从而瞬时利率围绕θ上下波动，体现了均值回复的特征.漂移项是rt的线性函数.

1.3 CKLS模型的最大似然估计（MLE）

从稳定性和有效性比较，MLE方法优于其他估计方法，用MLE估计参数更具有吸引力[5].Nowman[6]使用离散化的方法来估计CKLS模型，他首先将式（1）离散化，然后利用MLE对参数进行估计.Nowman的方法离散化后得到方程：

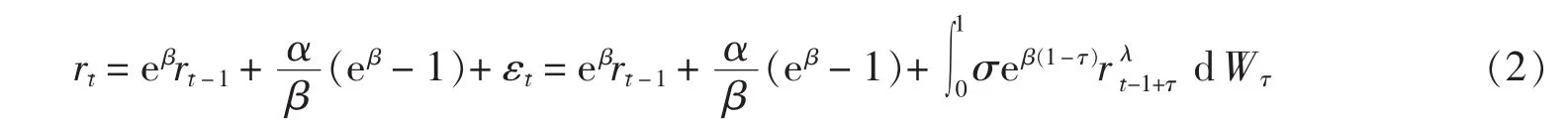
其中τ是微分变量，εt（t=1，2，…，T）满足条件:

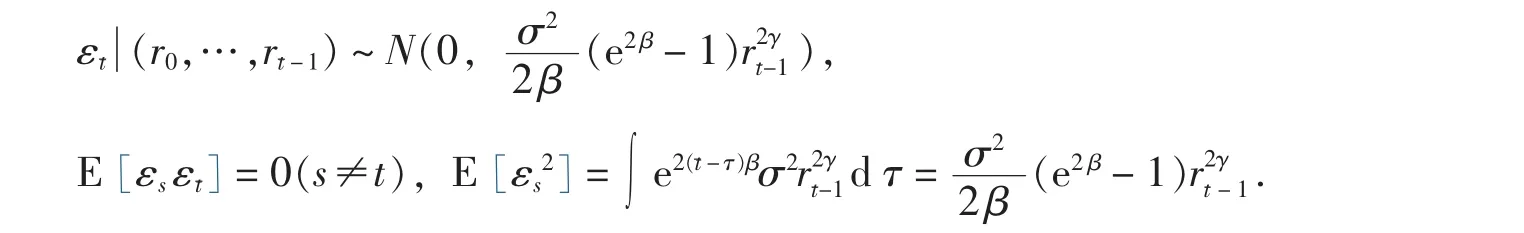
由式（2）可得到εt（r0，…，rt-1）的似然函数：

其中，f（rTrT-1，…，r0；Θ）为（rT，rT-1，…，r0）的联合概率密度函数，T表示当前这一期.f（ri+1ri；Θ）为转移密度函数，Θ为参数向量.

由于假设利率是一个扩散过程，所以离散化后的利率过程具有马氏性，在0时刻，t0已知，所以其概率密度函数f（r0）=1且εt（r0，…，rt-1）服从正态分布.将f（ti+1ti；Θ）代入，对式（2）的似然函数取对数，可得：

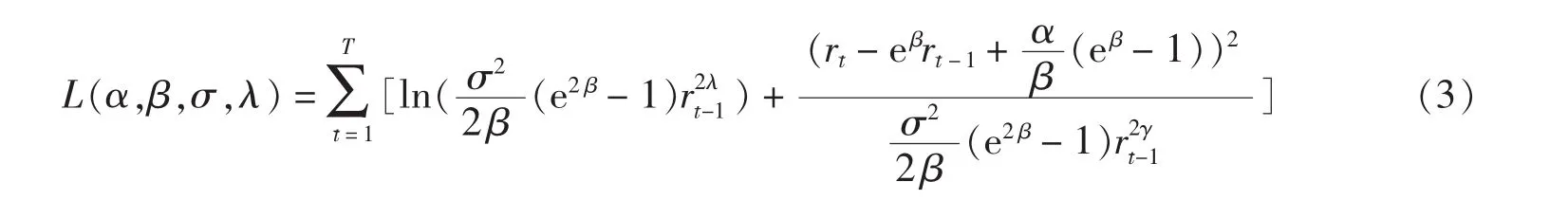
1.4 利率模拟的实证结果

上海银行间同业拆放利率（Shibor）的推出是中国利率市场化标志性的一步，是中国货币市场的基准利率.我们选取相对活跃且具代表性的1W-Shibor（品种为1周），时间范围从2006-10-12至2008-11-27，共778个交易观测值，数据是5日均值的加权平均利率.

利用EViews的最大似然估计LogL过程编程，可得到4个模型参数的估计和假设检验结果，见表1（数据来源：中国货币网http：∥www.chinamoney.com.cn／）.

表1 模型参数估计结果

对于Vasicek模型和CIR模型，3个参数的估计值在95%的置信水平上显著不为零.比较Vasicek模型和CIR模型的对数似然值和AIC准则，最终选取CIR模型来产生用于分析的模拟利率，并对其进行离散化.

对于式（1），代入CIR模型的参数，用差分代替微分，并取d rt=rt+1-rt，d t=1，其中dWt为标准正态随机变量，可得随机过程的离散形式：

基于式（4）可以产生用于VAR分析的模拟利率，模拟的方法采用MATLAB的蒙特卡罗模拟程序[7].

2 寿险产品定价的VAR分析

2.1 在险价值（VAR）

在险价值（VAR）是一种用于测量和控制金融风险的量化工具，Philippe Jorion将其定义为“VAR是在给定的置信水平下的一个持有期内的最大预期损失（或最坏情况下的损失）”[8]，即在一定的持有期和置信度内，某金融工具面临的最大潜在损失.

定义损失现值κ＝C+V+Q-G，其中，C表示保险给付的精算现值，V表示费用的精算现值，Q表示利润的精算现值，G表示毛保费的精算现值.

VAR可以表示为满足P（κ≤RVAα（κ））＝1-α的RVAα（κ），RVAα（κ）表示在给定概率1-α下产品的最大损失现值，α表示置信水平.模拟出大量利率路径，计算出κ的分布，由κ的分布得到RVAα（κ）的值.

2.2 随机利率下定期寿险毛保费模型推导

本文以半连续性产品为例，推导随机利率下的毛保费模型，这是传统寿险中最具代表性的保险产品，其保险金在被保险人的死亡时刻给付，而保费在期初缴纳，实务中也是如此.在这一节中所用的符号都是国际上通用的精算符号，对于x岁的人（x），半连续型且保险金额为1个单位的n年定期寿险，其趸交纯保费[9]：

其中E（ZT）为保险给付的期望值，bt为死亡给付保险金，ν（t）为利率折现因子，tpx·μx+t为（x）在t时刻死亡的概率.假定保单类型为k年缴费，且每年的附加费用率（包含了预期的利润因素）分别为αh（h=1，2，…，k），记均衡毛保费为.则：

由式（5）～（7）可以推导出该保单的均衡毛保费为：

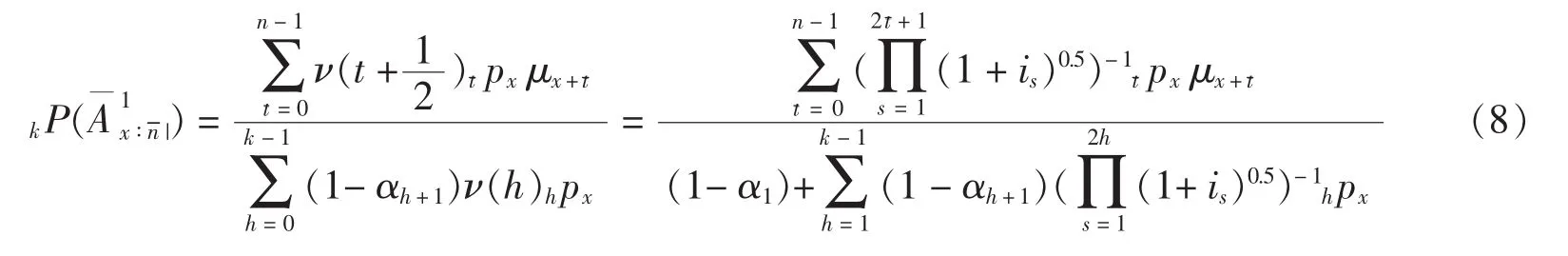
2.3 实例分析

利用式（4）模拟10000次，共3660天，并以半年为单位计算每个模拟路径半年的平均利率，作为定价的利率.蒙特卡罗随机模拟每次得到的路径都是不同的，由精算等价原理得到的是κ的一个分布，通过下面的例子进行分析.

假定35岁的被保险人，投保一份保险金额为1000元的10年期定期寿险，保费分5年缴纳，该产品的预定利率设为2.5%，死亡率采用我国非养老金男性生命表CL1（2000～2003）[4]，死亡发生在年中，并假设附加费用率如表2.

2.3.1 传统定价方法

利用传统方法，毛保费的确定如下：

表2 附加费用率

该保单单位保额年缴毛保费为3.632元.利用前面CIR模型得到的模拟利率，假设以3.632元为缴纳的毛保费，得到损失现值κ的分布，如图1所示.

由损失现值的分布，可以得到损失现值分布的数字特征，如表3所示.

由图1可以看出，以3.632元作为缴纳的毛保费，该产品出现亏损的概率非常小，当α＝5%时，RVA＝-0.055，即以3.632元作为收取的毛保费能以95%的概率保证该产品不但可以得到预期的利润，而且单位保额能赚取0.055元的超额利润，对于大保额保单，这种超额利润对实际利润的影响是比较大的.其中95%的含义表示100份相同的保单，有95份得到的利润比预期还要多.由表3可以看出，损失现值的期望为-0.163 4，即以该价格定价得到的超额利润现值平均为0.161 4，这说明该保单定价偏高.

2.3.2 加拿大资产负债方法

在随机利率下利用式（8）计算出毛保费的分布，对于蒙特卡洛模拟法，当模拟的次数足够多时，根据大数法则，价格将会趋于稳定.根据表1中CIR模型的参数，利用式（4）模拟10000次，可得到毛保费分布的数字特征，见表4.

由表4可以看出均值和中位数重合，峰度非常接近3，偏度接近0，分布接近正态分布.但是均值3.59元小于用固定利率2.5%计算的毛保费3.632元，这是因为用CIR模拟的利率表明目前市场上的利率被低估.

以均值3.59元作为缴纳的毛保费，得到损失现值的期望和中位数均为0.000 123，说明用保费均值定价，由于随机利率存在不利偏差，导致了定价出现亏损.实务中评估准备金时，如果使用的是随机利率，那么需要增加对利率的不利偏差准备，一般做法是为所有假设利率环境下所产生的准备金的期望值加上一倍方差（加拿大资产负债方法）[4].这启发我们，考虑毛保费的方差，以增加对利率的不利偏差准备，可得到新的保费：

图1 以3.632元定价的损失现值分布

表3 损失现值分布的数字特征

表4 随机利率下毛保费分布的数字特征

其中μ为随机利率下毛保费的均值，σ为毛保费的标准差，对于上面的例子，新的毛保费：

把缴纳的毛保费设定为3.591元，分析损失现值的VAR，如图2.

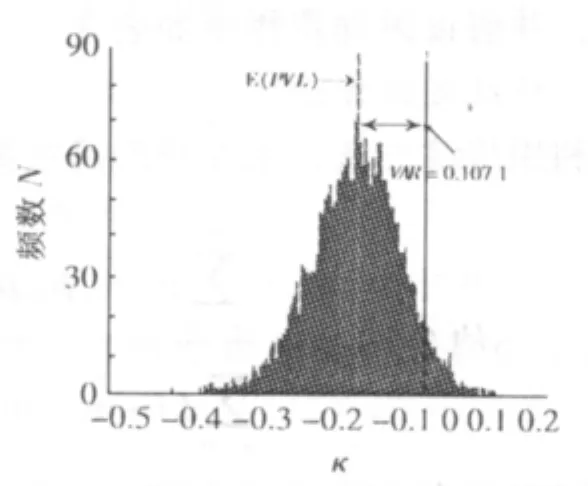
图2 加拿大资产负债法定价的损失现值分布

由图2可以看出，以3.591元作为毛保费，当α＝5%时，RVA＝0.107 1.即以3.590 9元作为实际缴纳的毛保费，能以95%的概率保证该保单的损失现值不超过0.107 1，而且损失现值期望为-0.000 001 327，非常接近于零，这说明采用加拿大资产负债方法的思想定价比固定利率定价更合理.

3 结语

虽然实务中定价采用的是预定利率，但是实际应用时可以用预定利率计算出毛保费，然后对毛保费进行VAR分析，通过设定α值和调整附加费用率的手段，得到VAR值，从而实现风险控制.如结果显示定价偏高，可以降低保费，以提高保单的销量，反之，提高保费，以满足定价充足性的原则.最后通过把加拿大资产负债方法的思想引入模型，得到了用毛保费均值加一倍方差作为定价毛保费能同时满足定价充足性和合理性的结论，为寿险定价提出一个新的思路.利用VAR分析其他产品时思路是一样的，可以用于资产份额法等定价方法的利率风险分析.

[1] Boyle P P.Rates of return as random variables[ J].Journal of Risk and Insurance，1976（18）：693-713.

[2] 吴金文，杨静平，周俊.随机利率寿险模型[J].经济数学，2001（18）：1-8.

[3] 赵静宇，郭士杰，罗传光.基于Vasicek模型下寿险产品定价研究[J].保险研究，2008（08）:44-47.

[4] 李秀芳.寿险精算实务[M].北京:中国财经出版社,2006:114-115.

[5] 潘冠中,邵斌.单因子利率模型的极大似然估计——对中国利率的实证分析[J].财经研究，2004，30（10）：62-70.

[6] Nowman B.Gaussian estimation of single-factor continuous time models of the term structure of interest rates[J].Journal of Finance，1997（52）:1 695-1 706.

[7] 石一磊.蒙特卡洛模拟在银行信用风险度量中的应用研究[D].苏州：江苏大学,2005.

[8] 魏宇.股票市场的极值风险测度及后验分析研究[J].管理科学学报,2008,11（1）：78-88.

[9] 卢仿先,张琳.寿险精算数学[M].北京:中国财政经济出版社,2006:128-133.

VAR Analysis of Life Insurance Pricing Risk under the Random Interest Rate

LIU Jia-jun，HUANG Shao-jie

(Department of Mathematics，Guangdong University of Business Studies，Guangzhou 510320,Guangdong，China)

The interest rates risk of life insurance pricing under the random interest rate is analyzed.First of all，the CIR model is selected as the basis to generate the simulated interest rates by the parameter estimation and hypothesis testing of random interest rate model.Then，a gross premium expression of regular life insurance under the assumption of random interest rate is derived.The minds of CALM are combined to measure the interest rate risk by using the VAR.

CKLS model；VAR；Life insurance；Random interest rates model；CALM

O 211.67

A

1001-4217（2010）01-0042-06

2009-09-02

刘家军（1974-），男，河南信阳人，讲师.研究方向：保险风险模型的理论与实证分析.E-mail:liu95828@yahoo.com.cn