二维赤潮生态数学模型及其在渤海的应用

李大鸣, 林 毅, 宋双霞, 解以扬, 韩素琴, 李培彦

(1. 天津大学 建筑工程学院暨港口与海洋工程教育部重点实验室, 天津300072; 2. 天津市气象科学研究所, 天津300074)

二维赤潮生态数学模型及其在渤海的应用

李大鸣1, 林 毅1, 宋双霞1, 解以扬2, 韩素琴2, 李培彦2

(1. 天津大学 建筑工程学院暨港口与海洋工程教育部重点实验室, 天津300072; 2. 天津市气象科学研究所, 天津300074)

采用ADI的有限差分方法对不可压缩流体二维浅水环流方程离散和求解, 建立水动力数学模型,用迎风格式离散赤潮生物动力学方程, 通过水动力学和生物动力学相结合的方法, 建立了二维赤潮生态数学模型。将所建立的二维赤潮生态数学模型应用于渤海, 针对渤海海域2004年6月11～16日发生的棕囊藻赤潮进行了数值计算。对EOS/MODIS卫星拍摄的2004年6月份的渤海海区卫星遥感图像进行了处理, 提取出海水中的赤潮信息, 并计算出赤潮面积, 使其与模型计算出的赤潮面积进行对比验证, 结果基本吻合, 表明该模型能够较好地模拟赤潮的生消过程, 为渤海地区的赤潮预报提供了科学依据。

二维赤潮生态数学模型; ADI法; 迎风格式; 棕囊藻; 渤海; 卫星遥感

对赤潮生态的研究迄今为止已有30多年的历史,从赤潮生物、生理、生化研究到赤潮生物发生机制研究以及赤潮预测预报研究, 所涉及的领域越来越深入, 要求也越来越高。越来越多的学者从赤潮生物的生理、生化特性、毒理学机制和发生机制、赤潮生物的生态环境以及赤潮的预测预报等方面对赤潮生物、赤潮的种类、赤潮发生与环境的关系展开了较为全面的探索。但是, 总的看来, 至今的赤潮研究主要还是集中在赤潮的生理、生态方面的研究, 因此要达到预报赤潮的发生还有漫长道路。

生态数学模型是赤潮研究的重要方法之一, 可以通过参数控制进行数值试验, 以便确定哪些因素在赤潮发生和发展的过程中起主要作用,既可以确定单个因素的影响, 又能对多因素的效果进行研究。齐雨藻、黄伟健等[1]对基础的统计学模型进行赤潮研究方面的工作。以微分方程为主要工具的赤潮生态动力学模型的研究工作始于Chen[2]、Ditoro[3]开发的简单的水质动力模型。在我国, 王寿春[4]等建立了这种生态动力学模型, 以种群生态学和营养动力学为依据, 提出了赤潮生物动力学研究对象之间的基本关系。但这些模型都没有考虑环境要素的影响, 特别是水动力环境的影响。

由于赤潮的成因相当复杂, 除了赤潮生物自身的特性外, 还涉及到物理、化学、水文、气象等诸多因素。为了对赤潮问题作更深入的研究, 必须借助动力学方法综合考虑各种过程以便从整体上探讨赤潮发生、发展的规律。如夏综万等[5]通过海洋动力学和赤潮生物动力学相结合的方法建立的大鹏湾夜光藻赤潮生态仿真模型。计算采取了ADI的方法,模型包括水动力、扩散和生物动力学三部分, 综合考虑了潮流、营养物质等环境要素的时空变化对赤潮过程的影响, 并以大鹏湾夜光藻赤潮为例进行了数值模拟。田峰等[6]针对近岸海域赤潮藻类生长及分布的特点,将简化了的赤潮藻类模型与水动力学中的对流扩散方程相耦合, 建立了一个水动力与生态耦合的赤潮藻类生长的深度模型。

要实现可靠的赤潮预报, 就必须将各种动力过程相结合, 从动态方面去阐明海洋赤潮高发区环境系统内赤潮生物生态过程、营养物质生物化学过程、赤潮生消的关键物理过程之间的定量关系等。这些只能通过数值模拟来实现。所以本文通过建立赤潮生态数学模型, 将水动力过程与生态动力过程相结合, 使较为可靠的赤潮预报成为可能。

1 水动力数学模型的建立

1.1 水动力数学模型的基本方程

1.1.1 基本控制方程

由 N-S方程推导出的不可压缩流体二维浅水环流方程为：

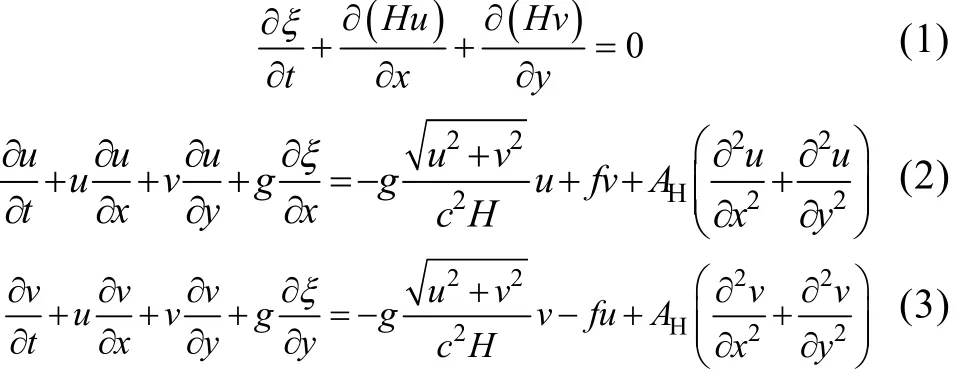
式中, 为增水位;Hhξ=+,h为水深;u为x方向的平均流速;v为y方向的平均流速;g为重力加速度;为谢才系数, 其中h是计算网格围点的水深平均值,n是粗糙系数, 即糙率, 由试验选取;f为柯氏力系数;HA为水平涡黏系数。

1.1.2 定解条件

岸边界条件：vn= 0 (n是边界法线方向)

ξ=ξ*(ξ*是已知边界的水位过程)

初始条件： 当t=0时,ξ=0,u=v=0

1.2 ADI的有限差分方法

本文对潮流场的数值模拟采用 ADI的差分方法(Alternating Direction Implicit Method)。它是一种显隐交替使用的有限差分格式, 其特点是将一个时间步长分成两个半步长计算, 在前半时间步长内,联立运动方程u分量方程和连续方程, 在x方向采用隐式差分求解 和u,y方向采用显式差分求解v; 在后半步长内联立运动方程v分量方程和连续方程,在y方向采用隐式差分求解 和v,x方向采用显式差分求解u。这样反复运用显隐交替的方法运算便能算出每个时间步长上各点的x和y方向的流速和水深。ADI法为一成熟的算法, 关于应用此方法对方程进行离散求解的具体过程见文献[7], 本文不再赘述。

2 赤潮生态数学模型的建立

赤潮生物动力学模型的基本方程在二维扩散方程基础上, 参考夏综万等[5]的赤潮生物动力学方程,考虑了速度修正的水平涡动系数xλ,yλ。

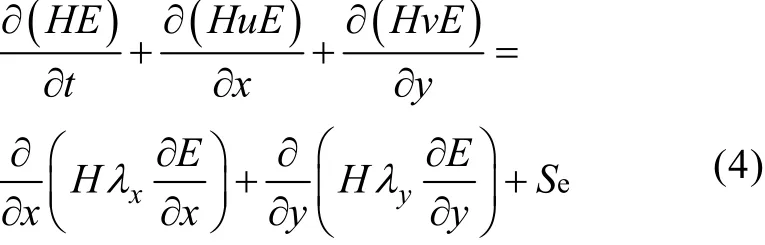
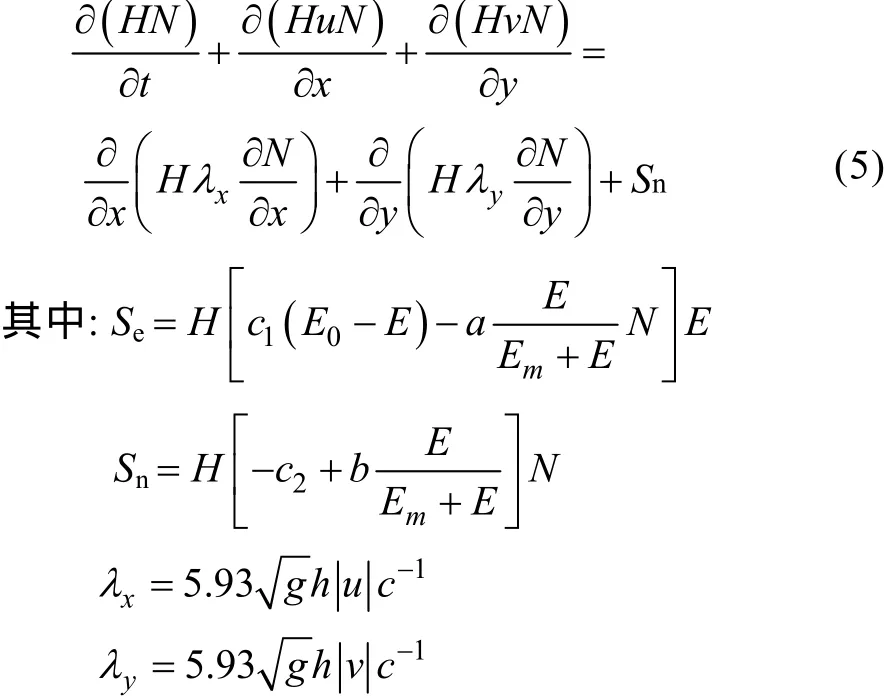
E为海水中营养物质的质量浓度;N为赤潮藻类的生物量密度;xλ为x方向涡动扩散系数;yλ为y方向涡动扩散系数; 其他各参数意义及其取值见表1。

表1 其他各参数意义及其取值Tab. 1 The significance and value of other parameters

其中,mE为营养物质的半饱和常数,是指可作为藻类细胞能正常生长所需维持水中有效形式营养盐的临界浓度, 也可用于比较不同浮游植物吸收营养盐能力的大小。在光强、水温及其他条件适宜而营养盐含量较低时,mE值越小的浮游植物越容易发展成为优势种;mE值越大的浮游植物会因缺乏营养盐使生长受到限制。以上的参数取值, 主要是参考了夏综万[5]、王洪礼[8]的取值, 并通过反复调试得出的结果。

迎风格式是一种最为常见的差分格式, 采用由下游向上游差分的方法代替微分, 离散方向和赤潮生态数学模型的扩散方向一致, 因此本文采用此方法, 对赤潮生物动力学方程进行离散, 具体方法见文献[7]。

3 二维赤潮生态数学模型在渤海的应用

3.1 二维平面水动力数学模型在渤海的应用

3.1.1 渤海概况[9]

渤海位于 37°07′～41°00′N、117°35′～121°10′E之间。它的东面有渤海海峡与黄海相通, 其余三面均为大陆所围。在我国行政区划上, 它的北界属于辽宁省, 西界属河北省和天津市, 南界为山东省, 东以辽东半岛的老铁山西南角与山东半岛的蓬莱间的连线——渤海海峡为界。是由辽东湾、渤海湾、莱州湾、中央盆地和渤海海峡五部分组成的。流入渤海的主要河流有辽河、海河、滦河、黄河等。渤海南北长约300 n mile, 东西宽约160 n mile, 沿岸所围的形状好似一个葫芦。渤海海域平均水深约18 m, 大部分海域水深较浅, 深度小于30 m的海域占总面积的95%左右, 海底地形平坦开阔, 5 m与25 m两级等深线最长, 平均坡度仅0°00′28″。水深大于30 m的海域大部集中在渤海海峡地区, 其中最大深度可达86 m。渤海的地形等深线图如图1所示, 图中等深线单位为m。

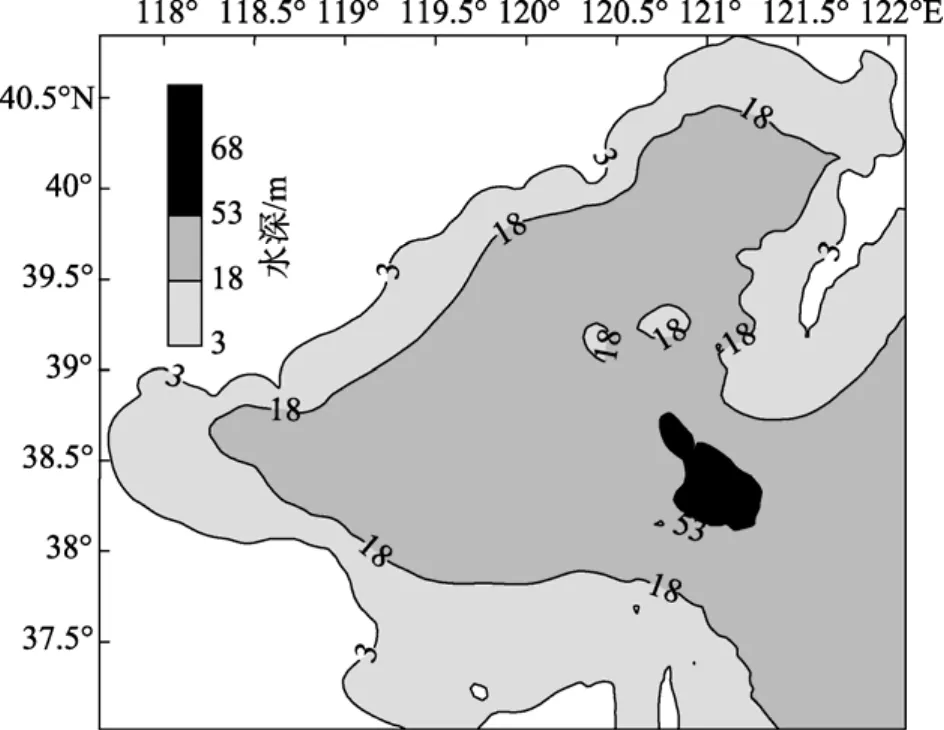
图1 渤海地形等深线图Fig. 1 Bathymetric chart of the Bohai terrain

3.1.2 模型网格的剖分

该模型仍采用ADI有限差分方法计算赤潮发生时各点水位及流速, 用正方形网格对计算区域进行剖分。考虑到模型范围仅覆盖了渤海, 因此计算网格相应加密, 采用的时间步长为60 s,空间步长为3 km, 剖分后为127列×142行。模型网格剖分图如图2所示。

3.1.3 流场模拟与流速验证

图2 渤海网格剖分示意图Fig. 2 Grid sketch of the Bohai Sea

为了准确模拟 2004年 6月渤海所发生的赤潮,作者运用该模型对渤海2004年5月30日7时到6月30日23时的水流潮汐进行了模拟计算。水边界条件采用边界点 P(97,60)、Q(84,25)(如图 2所示)在2004年5月30日7时到6月30日23时的潮位过程,其中括号中的数值表示网格位置坐标, 潮位过程如图 3所示。并在渤海取一点进行流速的大小及方向的验证。2004年5月30日7时开始后的第127 小时和第603 小时的流场示意图如图4所示。渤海测流点的流速和流向验证曲线如图5所示。

从以上验证曲线可以看出, 模型计算结果与实际基本吻合。尽管用于模型计算的实测资料有限, 以及计算中参数的概化与近似带来不可避免的误差,使得计算结果与实际有所偏差, 但模型计算所得的潮流场及潮位过程与实际情况的符合程度都比较令人满意, 可以作为进一步计算赤潮模型的基础。

3.2 二维赤潮生态数学模型在渤海的应用

2004年 6月 11日, 渤海海域出现棕囊藻赤潮,16日赤潮消失。棕囊藻隶属定鞭藻纲, 为广温广盐性藻类, 对环境有出色的适应能力。在世界各地的海洋中, 棕囊藻赤潮一般于春季爆发。从专业角度讲,1L海水中的棕囊藻密度要达到 1×107个, 才能称为赤潮。从2004年5月30日开始, 我们对模型进行了1个月的计算, 得到各时间段的藻类密度分布图, 图6为6月11日、16日的藻类密度分布图, 模拟了这 次渤海赤潮的生消过程。

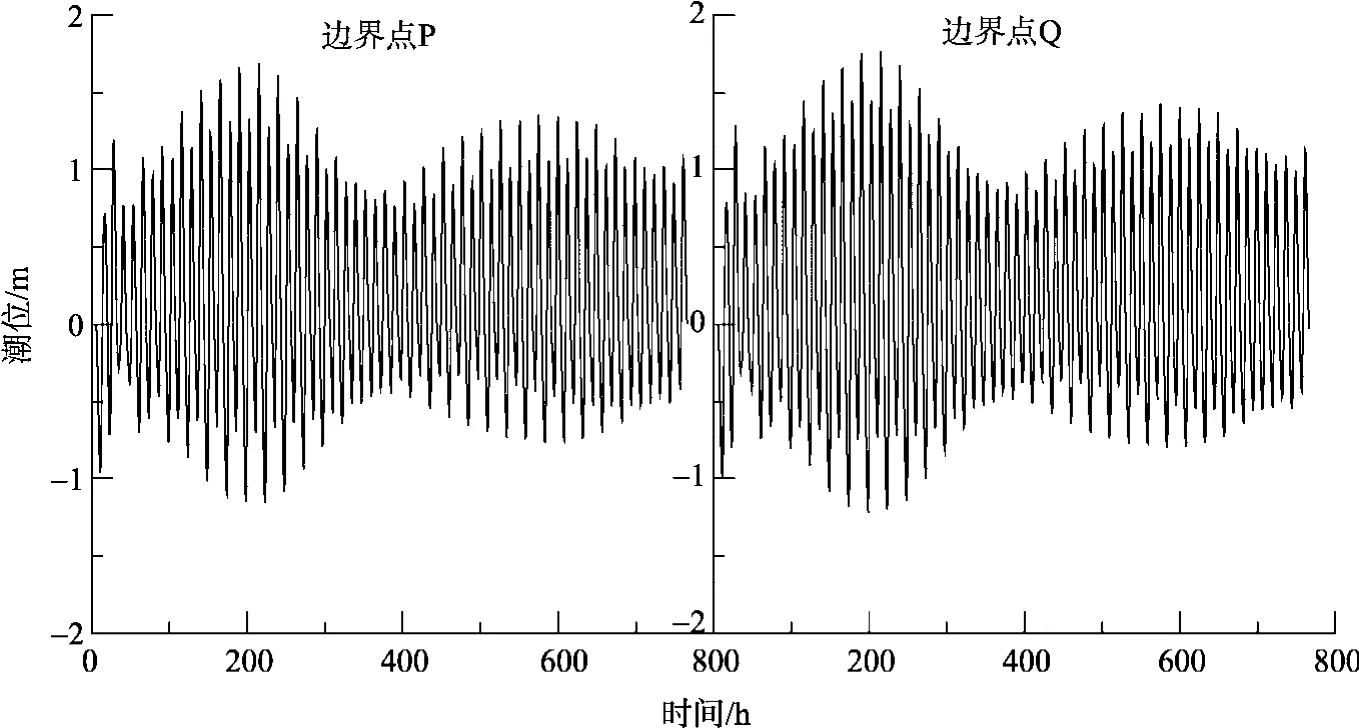
图3 边界点潮位过程Fig. 3 Tide process of border point

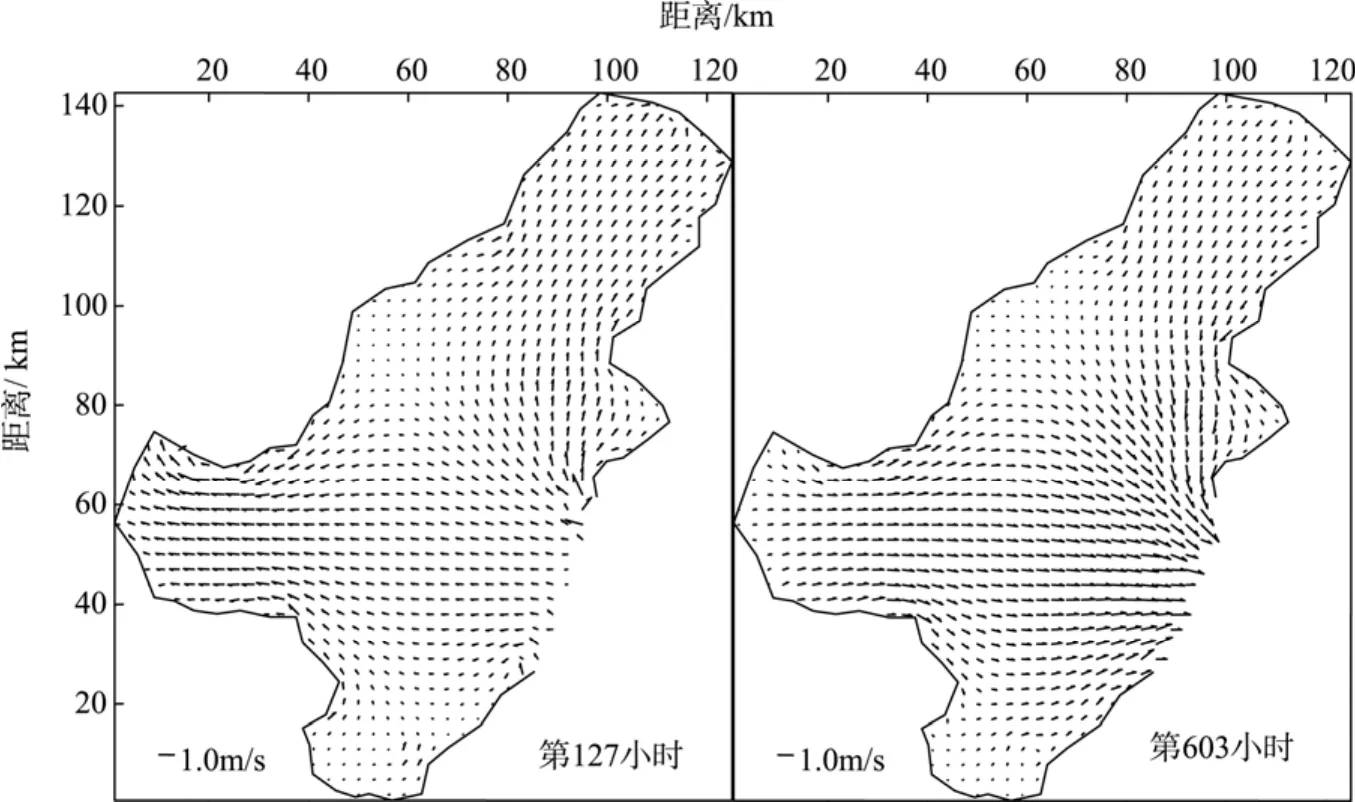
图4 流场图Fig. 4 Flow field

图5 测流点流速、流向验证Fig. 5 Velocity verification of measuring points

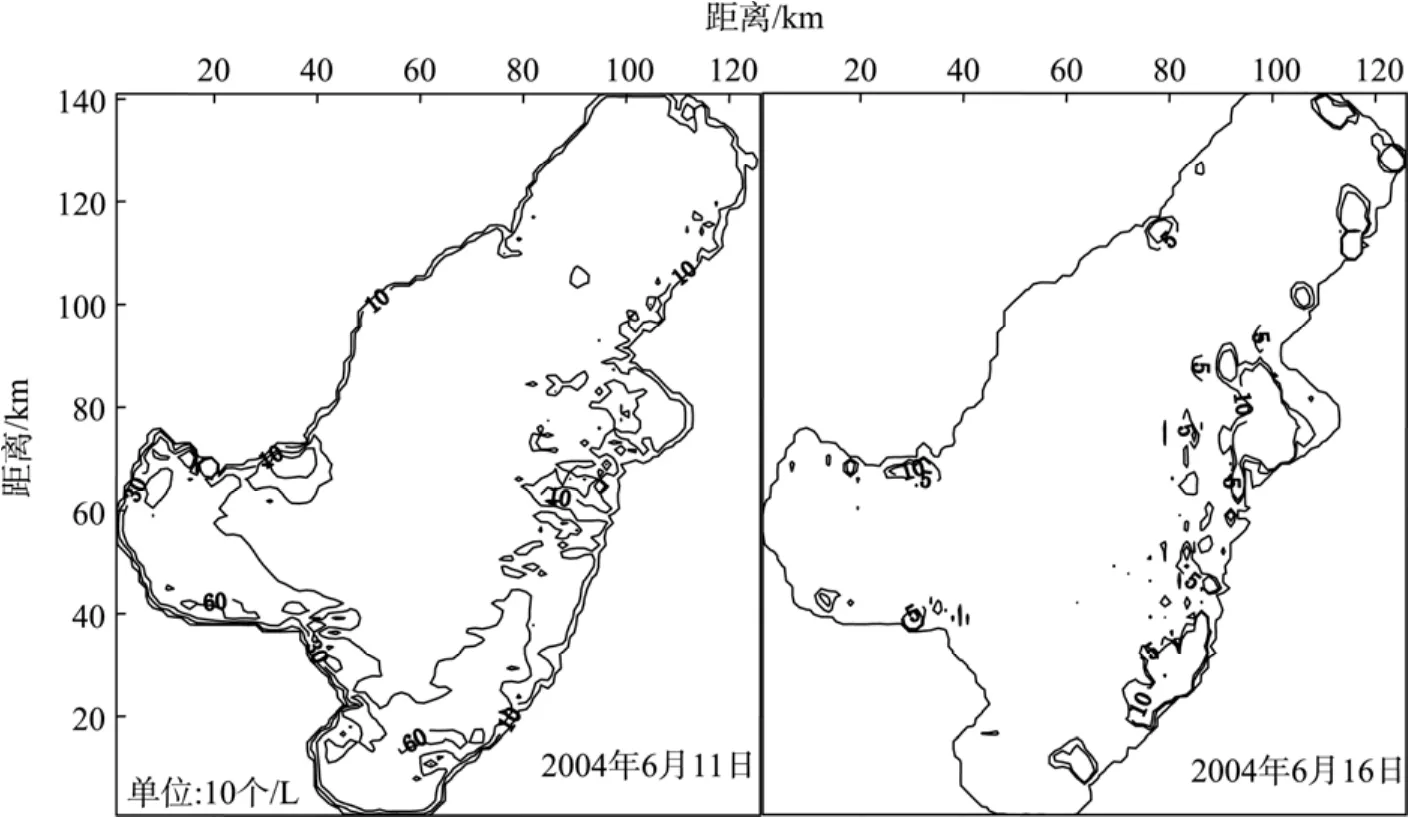
图6 藻类密度分布图Fig. 6 Distribution map of algae density

3.2.1 初始条件

初始时刻, 渤海海域内, 每一点的营养物质浓度都取为4× 1 0μg/L, 藻类密度都取为 0.1个/L。即：当t=0时, 取Ei,j= 4 × 1 0μg/L ,Ni,j=0.1 个/L。

3.2.2 从卫星遥感图像上提取赤潮信息

赤潮水体与非赤潮水体光谱相比具有明显的吸收峰和反射峰, 这些特征在卫星遥感探测上则会表现出在相应波段的离水辐射率(透射入水的辐射光经水分子、浮游生物、悬浮物等散射, 其中一部分离开水面反射出来, 这部分称为离水辐射率。)发生不同程度的增强或减弱, 而非赤潮水体在相应波段的变化较小。因此, 可以利用赤潮水体的这一特征作为赤潮是否发生的一个条件。

MODIS第三通道(459～479 nm)遥感信息中含有赤潮水体的吸收信息, 第四通道(545～565nm)遥感信息中含有赤潮水体的反射信息, 因此, 利用上述两通道反射率的比值建立如下算法用于提取海水中赤潮水体的信息。

其中,R3,R4分别是MODIS第三通道和第四通道的反射率,Cr是常数, 其值的大小与发生赤潮的海区和赤潮藻种有关。上式的比值在一定程度上表明海水表层浮游藻类的聚集程度, 也是水体中叶绿素a浓度的一种反映, 它随着水体藻类细胞密度的增加而增大。因此, 可以据此提取海水中的赤潮信息。

3.2.3 模型验证与结果分析

对EOS/MODIS卫星拍摄的2004年6月份的渤海海区卫星遥感图像(如图 7)进行了处理, 提取出海水中的赤潮信息, 并计算出赤潮面积, 使其与模型计算出的赤潮面积进行对比(如图8所示), 通过卫星遥感照片算出的赤潮面积大约是2 862 km2, 数值模拟算出的赤潮面积为2 637 km2, 面积大小基本相符,结果比较令人满意。

选择渤海内几个典型格点A(15, 44), B(46, 12),C(68, 63), 它们分别位于渤海湾、莱州湾及中央盆地(图2)。将这几点处的营养物质浓度E和藻类密度N的时间序列绘于图 9, 可以看出, 赤潮的发生与海洋中的营养物质浓度有着密切地关系, 即： 营养物质浓度大量增加后导致藻类急剧增殖, 而藻类的繁殖吸收了大量的营养物质又致使营养浓度转为下降,这和前人研究的结果一致[10～12]。从这几点的情况来讲, 处于渤海湾、莱州湾的这些地方, 似乎比渤海中开阔区域的部分, 如 C点更容易聚集营养物质和浮游植物, 因而更容易形成赤潮。这也说明了在这些地方潮流量级小, 扩散能力差, 营养物质容易聚集, 一旦产生了赤潮, 也不容易分散。这种趋势和这一带经常容易产生赤潮的情况相符[10]。

4 结论

图7 2004年6月11日MODIS渤海赤潮遥感图Fig. 7 Remote sensing map of the red tide in the Bohai Sea on June 11, 2004

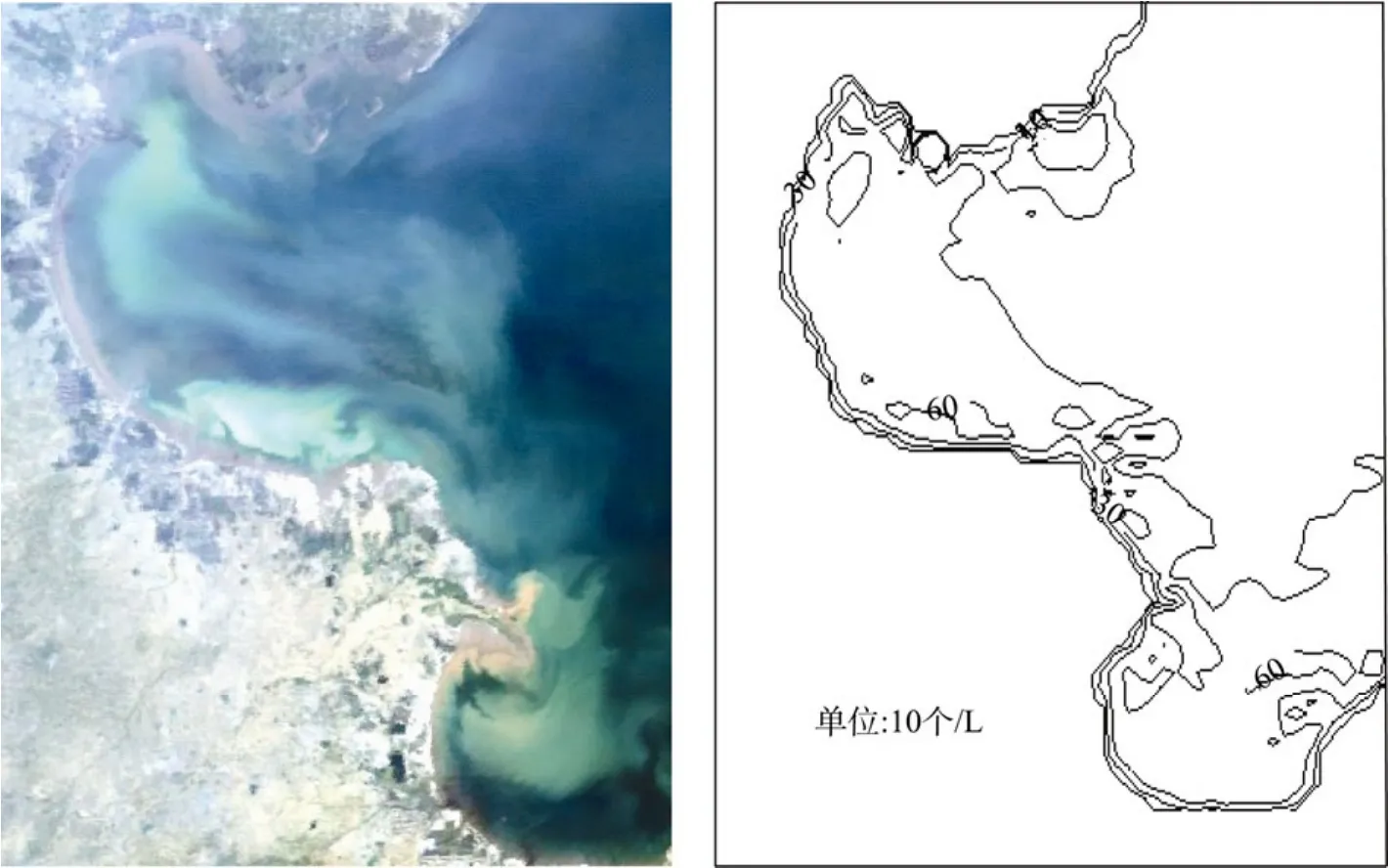
图8 赤潮扩散范围对比图Fig. 8 Comparison of the proliferation of red tide

图9 各个典型格点E和N的时空变化序列Fig. 9 Sequential changes of E and N in time and space of points

本文综合考虑了潮、流、营养物质对赤潮过程的影响, 建立了一个水动力学与生物动力学相结合的二维生态数学模型, 并以渤海棕囊藻赤潮为例进行了数值模拟, 对赤潮发生的数值模拟问题进行了初步尝试。

1)以不可压缩流体二维浅水环流方程为基本控制方程, 采用有限差分 ADI方法对方程进行离散,建立了渤海水流潮汐模型, 计算潮流场, 验证了测流点流速、流向, 取得了较好的模拟效果。

2)采用有限差分思想, 应用迎风格式对赤潮生物动力学方程进行离散, 建立二维赤潮生态数值模型并把该模型应用于渤海海区。

3)用该赤潮生态数值模型模拟验证了 2004年 6月11～16日发生在渤海的棕囊藻赤潮, 并与渤海海区赤潮卫星遥感图对比, 模拟结果与实测资料较吻合。

[1] 齐雨藻, 黄伟健, 邱璇鸿.大鹏湾夜光藻种群动态的时间序列模型[J]. 暨南大学学报, 1991, 12(3)：96-103.

[2] Chen C W. Concepts and utilities of ecologic model[J].Sanitary Engineering Division, 1970, 96： 1085-1097.[3] Di Toro D M, Oconnor D J, Thomann R V. A dynamic model of phytoplankton population in the Sacramento san Joaquin Delta[J]. Advances in Chemistry, 1971,106： 131-180.

[4] 王寿松, 刘子煌, 夏综万, 等. 封闭环境中赤潮发生过程的数学模拟[J]. 海洋与湖沼, 1998, 29(2)：163-168.

[5] 夏综万. 大鹏湾的赤潮生态仿真模型[J]. 海洋与湖沼, 1997, 28(5)： 468-474.

[6] 田峰, 葛根, 杨晨. 水动力与生态耦合的赤潮藻类生长模型研究[J]. 海洋技术, 2007, 26(2)： 34-37.

[7] 李万平. 计算流体力学[M]. 武汉： 华中科技大学出版社, 2004. 160-182.

[8] 王洪礼. 渤海赤潮藻类生态动力学模型的非线性动力学研究[J]. 海洋技术, 2002, 21(3)： 8-12.

[9] 中国科学院海洋研究所海洋地质研究室. 渤海地质[M]. 北京： 科学出版社, 1985. 1-44.

[10] 齐雨藻. 中国沿海赤潮[M]. 北京： 北京出版社, 2003.1-302.

[11] 钱宏林. 南海北部沿海夜光藻赤潮的生态模式研究[J]. 生态科学, 1994, 1： 39-46.

[12] 王寿松, 刘子煌, 夏综万, 等. 封闭环境中赤潮发生过程的数学模拟[J]. 海洋与湖沼, 1998, 29(2)： 163-168.

Two-dimensional ecological mathematical model of red tide and its application in the Bohai Sea

LI Da-ming1, LIN Yi1, SONG Shuang-xia1, XIE Yi-yang2, HAN Su-qin2, LI Pei-yan2
(1. Tianjin University School of Civil Engineering & Key Laboratory of Harbor & Ocean Engineering Ministry of Education, Tianjin 300072, China; 2. Institute of Tianjin Meteorological Bureau, Tianjin, 300074, China)

Mar., 9, 2009

two-dimensional ecological mathematical model of red tide; ADI method; upwind scheme; Phaeocystis; the Bohai Sea; remote sensing

The two-dimensional ecological mathematical model of red tide was established by combining water dynamics with biological dynamics. The water dynamics mathematical model was established by dispersing and solving the incompressible two-dimensional circulation equations in shallow water by the ADI (Alternating Direction Implicit) Method of the finite difference method, and the red tide biodynamic equations was dispersed by upwind scheme. The established 2D ecological mathematical model of red tide was applied to calculate the red tide of Phaeocystis, which occurred in the Baohai Sea during the period of June 11～16th, 2004. Satellite remote sensing data of the red tide area and calculation results based on the model were in good agreement. It shows that the model can simulate the process of growth and death of red tide well and provide scientific basis for red tide forecast in the Bohai Sea.

X55

A

1000-3096(2010)09-0087-07

2009-03-09;

2010-07-05

李大鸣(1957-), 男, 河北枣强人, 教授, 博士, 博士生导师, 主要从事水力学及河流动力学、海岸工程, 电话： 022-87401579,E-mail： lidaming@tju.edu.cn

(本文编辑： 刘珊珊)