一类固定工件排序问题算法研究

□汪 瑜 孙 宏 [中国民航飞行学院 广汉 618307]

一类固定工件排序问题算法研究

□汪 瑜 孙 宏 [中国民航飞行学院 广汉 618307]

针对一类“可用机器数有限,存在机器与工件间匹配约束,以机器-工件分配成本最小为目标”的固定工件排序问题，以固定工件的开始时刻、结束时刻为基准构建网络时序图，将“机器-工件”分配过程看成网络时序图中的网络流问题，并设计排序问题的模拟退火算法。通过算例发现：算法平均CPU时间为32.9秒，总成本最大误差为0.07%，时间复杂度为O(M(m3+ mn))，空间复杂度为O(m2n)。结果表明：算法为多项式算法，且可行。

固定工件排序；网络时序图；模拟退火；多项式算法

引 言

固定工件排序问题是指对拥有明确加工时间的若干待加工工件，将其按照一定的加工顺序分配给机器加工，实现最小化工件的最大完工时间。而作为一类特殊的固定工件排序问题，即有机器数目限制，开始时刻与结束时刻明确，存在“机器-工件”约束关系的问题同样在经济管理、生产调度、工程技术和军事方面有着广泛的应用背景：如在学校课程表的制定过程中，所有的待授课程（即固定工件）有着明确的开始时刻与结束时刻，而教室（即机器）数目是有一定限制的，并存在待授课程的学生数目与教室可容纳人数之间的限制问题，要求合理安排待授课程与教室之间的关系；又如航空公司飞机调度问题，在已有的航班计划基础上，航班（即固定工件）的起飞时刻与结束时刻等因素明确，待使用飞机（即机器）数目有限，另外航班上的旅客人数与飞机最大容量之间存在着一定的约束，要求合理的将飞机分配安排到航班上；又如企业人员调配问题中，在工作计划中合理的选择做事顺序，以及铁路运输中的调机分配问题等均可归入到此类固定工件的排序问题之中，甚至宇宙飞船复杂庞大的飞行计划编排,都要用到上述的排序理论和算法。显然此类排序算法对解决自然界与社会中存在的问题有着巨大的现实意义。然而根据现有的研究成果发现，这种“有机器数目限制，开始时刻与结束时刻明确，存在“机器-工件”约束关系，以加工的总成本最小为目标”的固定工件排序问题是NP-Complete（NPC）[1]问题且不存在好的多项式算法，为此寻找好的启发式算法成为了解决这类问题的关键。

最早提出此类固定工件排序问题启发式算法的U.I.GUPTA设计了一种求解该类问题的贪婪算法并解决了电路线路安排问题[2]，随后M.Fischetti在U.I.GUPTA的基础上，进一步研究了公共汽车司机的排班问题[3～5]，K.Jansen的航空公司飞机维护人员排班问题以及V.Gabrel的地球观测卫星轨道选择问题等均使用了贪婪算法[6～7]，Qiwei Huang等人设计了一种考虑不同类型机器加工工件成本不同的算法，该算法认为加工时间与加工成本呈线性关系，并指出在仅有2种机器类型时设计的近似算法为多项式算法，超出2种类型时仍为NPC问题[8]。对于此类特殊的固定工件排序问题，国内的洪文等人通过将数学模型与数据分离的形式进行了研究，并用LINGO软件给出了一种实用算法[9]，孙宏等人按照固定工件加工开始、结束时刻构造了工件时序网络模型，并将固定工件排序问题转化为网络流模型[10]。

然而，“有机器数目限制，开始时刻与结束时刻明确，存在“机器-工件”约束关系，以加工的总成本最小为目标”的固定工件排序问题现有的研究成果并没有考虑到机器资源限制，且给出有效的多项式算法，因此并不能很好地应用到现实问题中。本文首先通过构造以固定工件时刻为基础的网络时序图，并以此得出基准的机器资源限制，随后以时序网络模型的路径分配成本最小为目标函数设计基于模拟退火的启发式算法并给出复杂度公式，最后通过算例对算法进行分析。

一、算法设计

（一）算法原理

在此类固定工件排序问题中，每个工件将被分配到不同的机器上进行加工作业，目标是求出所有工件的加工方案使得完成全部加工的总成本最小。对于每一个工件来说，它要在不同的机器上进行加工，且不同的机器加工同样工件的成本不同。虽然我们无论如何都可以求出工件的加工方案，但是如果安排不当就会出现工件在加工成本较高的机器上加工导致成本上升，这样就会使得完成全部工件加工的总成本较大。由于工件加工时间具有先后顺序，因此这使得工件排序问题变得更加复杂。首先通过建立描述固定工件时序关系的工件网络时序模型来确定工件之间加工的先后顺序，然后再将机器分配到由网络时序图所构造的有向路径上，即将固定工件排序问题转化为寻找工件网络模型的最优有向路分解问题，并以时序网络模型的路径分配成本最小为目标函数，构造了一种基于模拟退火的启发式算法。具体来说：

第一步：构造工件的网络时序图。根据所有“待加工工件”加工的开始时刻、结束时刻，以“连续的结束时刻与紧随其后的连续开始时刻看成一个节点(阶段)”的原则，将所有的“时刻”归入不同的节点(阶段)中，并以每一个待加工工件的开始时刻和结束时刻所在的节点以有向弧连接，将节点总数记为t。检查除起点与终点以外的任一节点vi(i=2，3…t-1)，记其出度与入度之差为k。若k〈0，则连接vj到vj+1(j=1，2…i-1)共k条虚弧；若t〉0，则连接vj到vj+1共k条虚弧。以此保证节点vi(i=2，3…t-1)出、入度相等；

第二步：有向路径的分解方案。根据第一步生成的网络时序图，可以得出图的最大割，记为z，生成z条均以第一个节点开始、最后一个节点为终点，包含不同“弧”的有向路径；

第三步：构造评估函数。根据第二步中的有向路径分解方法，将可供选择的“机器”数，记为n，分配给z条有向路径。显然不同的“机器”加工不同的“有向路径”的成本是不同的，寻找最优的“机器-有向路径”分配方案。并将每一个“机器”数量累计，得出所需的“机器”与其对应的数量；

第四步：利用模拟退火设计启发式算法。将有向路径的分解方案看成“状态”，将最优的“机器-有向路径”分配成本看成评估函数。通过随机生成不同的“状态”以及得到不同的评估函数值，不断的转移“状态”(退火)，在达到算法的终止准则时，停止“状态”的转移并得出最佳方案。

对于算法的详细过程，可参考文献11，12。

（二）参数选取

上述基于模拟退火算法的参数主要包括了初始温度t0，算法终止温度tf，温度最大下降次数Mmax以及最优解保持次数Ccount。为了保证算法稳定的收敛，对参数进行仿真分析。按照起始温度应能保证平稳分布中每一状态的概率相等的原则，算法选取的终止温度为tf=10，初始温度t0=Kδ，K是一个充分大的数，δ={max{cij}-min{cij}}z，其中max{cij}所形成的“候选机型-有向路径”最大成本函数值；min{cij}表示所形成的“候选机型-有向路径”最小成本函数值；z表示有向路径数[11]。图1、图2是在操作系统Windows Vista， MATLAB7.0环境下，内存1G，CPU主频1.83GHz，硬盘空间80G下分别对温度最大下降次数Mmax与最优解保持次数Ccount的仿真实验，从图1中可以看出，对于“5架机器，33个固定工件”问题温度最大下降次数Mmax在达到60000次后对于最优解的影响已经趋于稳定，而对于“10架机器，68个固定工件”问题温度最大下降次数Mmax在达到90000次后对于最优解的影响已经趋于稳定。即对于规模在“60个固定工件，10架机器”以下的问题，选取温度最大下降次数Mmax=90000次足可达到稳定。类似地，另外从图2中可以看出，对于规模在“60个固定工件，10架机器”以下的问题，最优解保持次数Ccount选取900次即可保证算法达到稳定。

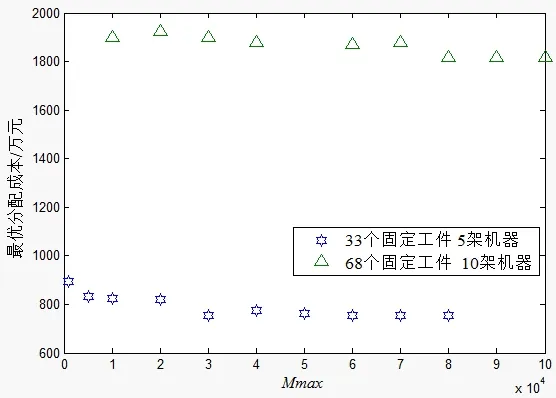
图1 最大迭代次数对解的影响

（三）算例

为了验证算法，本文采用航空公司机队规划问题进行分析。基于航班机型分配的航空公司机队规划是典型的此类特殊固定工件加工问题：“工件”即为航班节(一个航班节由多个航班组成)[12]，“机器”即为飞机机型。工件的开始时刻、结束时刻明确，分别为航班的起飞时刻以及到达时刻，目标为机队规划的总分配成本最小。

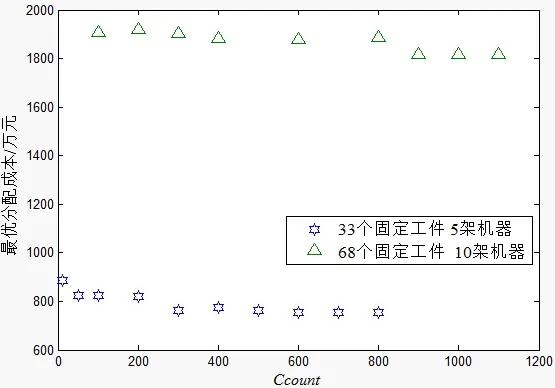
图2 最优解保持次数对解的影响

通过上述分析，选取t0=9000，tf=10，Mmax=90000，Ccount=900，对“7种机型，58个航班节”进行计算，结果如图3所示，横坐标是“航班节”的时刻表，图中的任一“行”为航班节的飞行顺序以及所使用机型。算例中需要的飞机总数为30架：其中机型2：1架；机型3：3架；机型4：26架；总成本为1484万元。

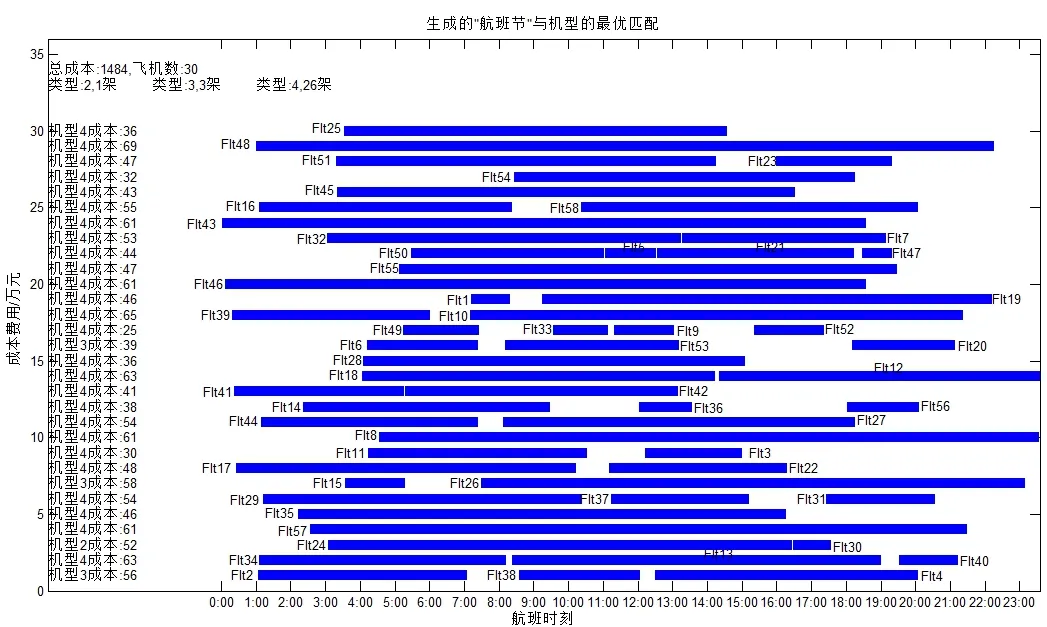
图3 航空公司机队规划方案

为了对机队规划算法的运算效率进行评估以及验证计算结果的稳定情况，经过10次的仿真，结果如表1所示，计算出平均的CPU时间为32.9秒，总成本最大误差为0.07%。

二、算法复杂度

算法时间复杂度主要由有向路径的随机生成与最优的“有向路径-机器”分配决定。对于随机生成的z条有向路径，其最好的情况下是所有的工件均可以在时间上相连，即m+1=t，其中m为工件数目，t为网络时序图中节点数目；而最坏的情况是所有的工件均不可以相连，即节点v1的出度=m =z。因此在网络时序图上的节点vi(i=1，2…t)上随机地选择发出弧，其最大的出度为工件数m。而网络时序图节点总数t的最大值为m+1，因此生成一条随机路径的复杂度可以表示为O(m2)，即生成z条有向路径的时间复杂度为O(m3)；而对于“有向路径-机器”分配方案，其时间复杂度显然与可供选择的“机器”数以及有向路径数有关。若可供选择的“机器”数为n，那么其算法时间复杂度应为O(mn)。因此若在模拟退火算法迭代的过程中最大的迭代次数为M，那么整个算法的时间复杂度应该为O(M(m3+ mn))。对于算法的空间复杂度而言，完全取决于所构造的网络时序图中的“有向路径”数以及可供选择的“机器”数，因此空间复杂度为O(m2n)。

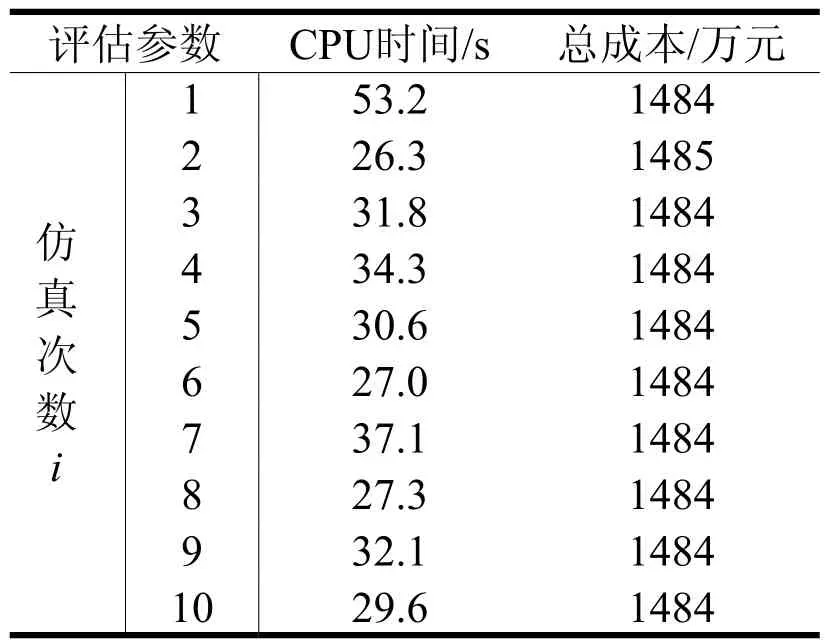
表1 算法CPU时间与成本函数值仿真

三、结 语

针对“机器资源有限，加工时间确定、机器与工件有约束关系以及以最少加工成本为目标”的一类固定工件排序问题，本文根据工件的加工时刻构造网络时序图，将固定工件排序转化为网络时序图中的网络流问题，并利用模拟退火进行算法设计。通过算例发现，算法平均计算时间为32.9秒，总成本最大误差为0.07%，算法的时间复杂度为O(M(m3+mn))，空间复杂度为O(m2n)。以此解决了现实中该类问题不存在有效多项式算法的缺陷。

另外必须说明的是，这类特殊的固定工件排序问题，能够广泛应用于航空企业中的机型分配，基于航班机型分配的机队规划问题，另外也适用于企业人员的调度、火车调机分配、学校课程表制定等问题，因此具有良好的应用前景。

[1] 朱一清. 可计算性和计算复杂性[M]. 北京: 国防工业出版社, 2006.

[2] GUPTA U I, LEE D T, LEUNG J Y T. An optimal solution for the channel-assignment problem [J]. IEEETransactions Computers, 1979, 28(11):807-810.

[3] FISCHETTI M, MARTELLO S, TOTH P. The fixed job scheduling problem with spread-time constraints [J].Operational Research, 1987, 35(6): 849-858.

[4] FISCHETTI M, MARTELLO S, TOTH P. The fixed job scheduling problem with working-time constraints [J].Operational Research, 1989, 37(3): 395-858.

[5] FISCHETTI M, MARTELLO S, TOTH P.Approximation algorithms for fixed job schedule problem [J].Operational Research ,1992 ,40(Supp.No.1):96-108

[6] JANSEN K. An approximation algorithm for the license and shift class design problem [J]. European Journal Operational Research, 1994, 73(1):127-131.

[7] GABREL V. Scheduling jobs within time windows on identical parallel machines new model and algorithms [J].European Journal Operational Research, 1995, 83(2): 320-329.

[8] HUANG Qi-wei, LOYD E. Cost Constrained Fixed Job Scheduling [C]. Lecture notes in computer science2841, 2003:111-124.

[9] 洪文, 胡雁玲. 工作排序问题及其数学模型[J]. 合肥联合大学学报, 2002, 12(1): 95-99.

[10] 孙宏, 杨伟, 黎青松, 文军. 固定工件排序问题的网络流模型研究[J]. 西华大学学报, 2006, 25(1): 20-22.

[11] 孙宏, 文军. 航空公司生产组织与计划[M]. 成都:西南交通大学出版社, 2008: 69-74.

[12] 孙宏. 航空公司飞机排班问题：模型及算法研究[D].成都: 西南交通大学, 2003.

Research on the Algorithm of One Class of Fixed Job Scheduling Problem

WANG Yu SUN Hong
(Civil Aviation Flight University of China Guanghan 618307 China)

For one class of fixed job scheduling problem, in which the available processors were limited, the processor matching-job had to be considered and minimized processor matching-job assigning cost were taken as objective. Firstly, based on the starting and completing time of the fixed job, this algorithm constructed a network time sequence figure. Secondly, the processor matching-job assigning were transformed into a netwok flow problem. Thirdly, the simulated annealing was used to design the scheduling problem algorithm. The solid example shows that the average CPU time is 32.9 seconds, the maximum error of total cost is 0.07%, the time complexity is O(M(m3+ mn)), and the space complexity is O(m2n). The results indicate that this algorithm is polynomial and feasible.

fixed job scheduling; network time sequence model; direction route; polynomial algorithm

F273

A

1008-8105(2010)03-0019-04

编辑 范华丽

2009 − 09 − 24

国家自然科学基金资助项目( No.60776820),中国民航飞行学院自然科学基金(J2008-76),中国民航飞行学院自然科学基金(J2009-29)

汪 瑜(1983 − )男，工学硕士，中国民航飞行学院教师；孙 宏（1966 −）男，工学博士，中国民航飞行学院教授.