分形闪电通道模型的建立及其电磁辐射特征

张其林,冯建伟,赵中阔,卞建春

(1.南京信息工程大学气象灾害省部共建教育部重点实验室,江苏南京 210044;2.南京信息工程大学大气物理学院,江苏南京 210044;3.中国科学院大气物理研究所中层大气与全球环境探测开放实验室,北京 100029)

分形闪电通道模型的建立及其电磁辐射特征

张其林1,2,冯建伟1,2,赵中阔3,卞建春3

(1.南京信息工程大学气象灾害省部共建教育部重点实验室,江苏南京 210044;2.南京信息工程大学大气物理学院,江苏南京 210044;3.中国科学院大气物理研究所中层大气与全球环境探测开放实验室,北京 100029)

基于高速摄像系统获取的自然闪电通道形状,利用分形方法构建了分形闪电通道模型,分析计算了闪电通道的弯曲对地面附近不同方位、不同距离处回击电磁场的影响。结果表明,在100 m到10 km的近距离范围,不同方位的回击垂直电场峰值之比为0.8～2.3;而当距离增加时,这种差别逐渐消失。但无论距离远近,地面水平磁场随方位角都存在较明显的差异,不同方位的回击磁场峰值差异达到2～4倍。与假定通道笔直的回击模型相比,分形闪电通道模型能很好地再现回击过程电磁辐射的高频分量和次峰等细微现象。

回击;通道形状;分形;垂直电场;辐射场

0 引言

地闪回击过程产生的微秒、亚微秒量级的高频电磁脉冲(LEMP)对星载仪器、飞机导航设备的正常运行,及地面电网、通信和控制设备等具有极强的破坏作用,人们一直注重雷电电磁辐射精细结构的研究。不过,有关地闪回击过程电磁辐射的计算,通常假定通道笔直且垂直地面,地面无限光滑且电导率无限大。这样的简单模型只能大致地模拟地闪回击电磁场波形的基本特点(即上升快、下降缓慢),却无法精细地刻画回击电磁场波形的次峰和振荡等特点,也无法模拟回击过程的频谱分布尤其是高频分量,这对研究雷电电磁辐射与高压输电线之间的耦合机制等许多方面造成较大困难。

Hill[1]最早利用高速摄像技术对回击主放电通道的弯曲进行了统计分析,发现主放电通道方向的改变满足高斯分布,弯曲的水平距离平均为1 km,通道方位角平均变化为16°。随后,Hill[2]利用实际观测的闪电通道,理论计算发现通道的弯曲会引起VLF频段电磁波能量的增加。1978年LeVine和Meneghini[3]利用蒙特卡诺方法生成了闪电通道,研究了回击通道的弯曲对远距离辐射场的影响,结果表明通道的弯曲使得回击的频谱分布超过100 kHz,通道越弯曲,相应的高频电磁辐射越强。1994年Vecchi等[4]研究发现,在一定精度范围内,闪电通道是分形的,其时域辐射场也是分形的,且辐射场的分形维数与通道维数基本一致。1997年Valdivia等[5]利用分形理论,发现地闪回击通道可近似看作分形天线,其电磁辐射瓣膜和强度与偶极子辐射天线明显不同。2003年祝宝友等[6]假定闪电通道垂直上升2 km,之后沿水平方向发展,在水平方向1.5 km处出现不同方向的分叉,研究发现地闪回击通道的弯曲能明显增加高频辐射分量。

从上述研究结果看出,作为描述混沌现象的有力几何工具——分形理论已经成功地应用于闪电放电过程。不过,闪电放电的分形特征是从工程应用的角度来分析研究的,而不是从数学角度上,因为数学上的分形性必须满足无限精细的自相似。从宏观上看,分形理论是描述闪电通道形状、闪电电磁辐射、地闪放电的接地过程等许多复杂现象的有力工具。但上述研究大多数采取了Fraunhofer的远场电流矩的近似方法,而当距离较近时,静电场和感应场分量为主,上述结果不再适用。且由于闪电通道的分形特点,在距闪击点不同方位测量的电磁场不同,相应地利用地面电磁场反演雷电回击电流参数时可能存在较大差异。

因此,本文利用野外观测实验中高速摄像系统获取的自然闪电通道形状,以及根据分形理论模拟的闪电通道,拟建立一种分形闪电回击通道模型,并利用该模型讨论通道的弯曲对时域回击电磁场峰值和波形等参数的影响。

1 任意弯曲闪电通道回击辐射场的计算方法

如图1所示,假定回击脉冲电流以接近光的速度ν沿一任意弯曲的通道向上传输,P(x,t)为自由空间的观测点,idl为某一时刻的电流元,θ为电流元与矢径r的夹角。回击通道的辐射可以看作是由无穷多个时变电偶极子组成,所以观测点P(x,y,θ,t)矢势为

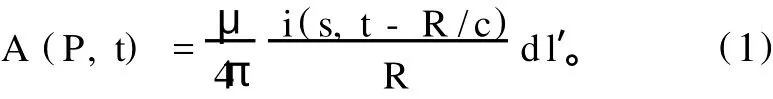
利用洛伦茨变换,可得标势

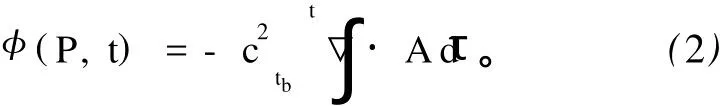
其中,tb为电磁脉冲到达观测点的时间。因此

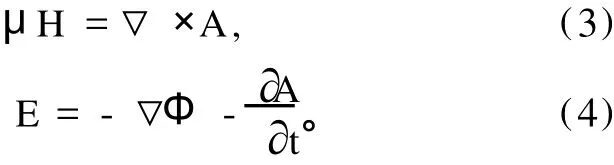
在笛卡尔坐标系中,(3)和(4)式可写为

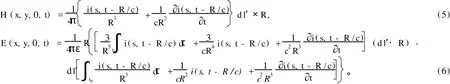
其中,v=1.5×108m/s为回击速度。将观测点P(x,y,0,t)在t时刻看到的表观通道长度L′(t)分解为许多个偶极子,则总的电磁场为

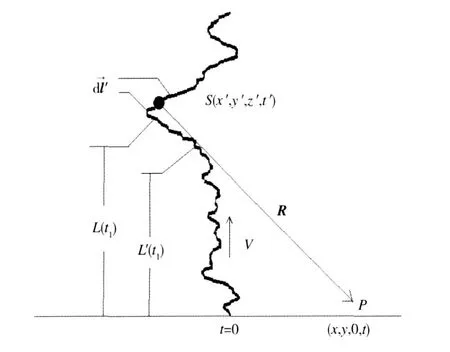
图1 分形闪电通道电磁场的计算示意图Fig.1 Schematic diagram of a fractal lightning channel and the corresponding calculation of electromagnetic fields

2 分形闪电通道的模拟及其分形维数的确定

2.1 闪电通道分形维数的确定

地闪先导的传输沿空间电势的梯度方向,而空间电势与大气电导率和空间电荷密度的分布密切相关。因此,由于强对流天气过程的复杂性,不同地区的雷暴过程以及同一地区的不同雷暴过程的地闪先导发展通道差异较大。为了确定地闪通道的弯曲特征,本文选取了不同地区的闪电通道进行分析。图2a是在青海地区利用高速摄像系统拍摄的一次闪电通道,观测距离约为7km;图2b是经过图像处理方法获得的闪电通道。从图中可以看出,经过图像处理方法获得的闪电通道与原图是非常接近的。确定弯曲闪电通道分形维数的方法一般是数盒子法[7-8],即将考查的曲线所在平面按统一尺度,沿两个垂直方向归一化,选取一定的分割间隔ri将平面分成小方格,数出曲线坐落于小方格的个数NI,则曲线的分形维数D为

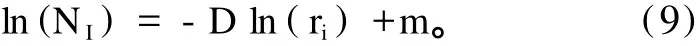
其中,m为方盒形状因子。不过,利用这种方法计算的分形维数与选取的网格大小密切相关。如图3所示,选取的网格步长不同,计算的通道弯曲程度也不同。步长小于20m时,平均弯曲随步长增大而增加;步长大于20m时,平均弯曲随步长增大而减小。M onte-Carlo模拟方法表明,计算弯曲通道分形维数的理想步长应选择峰值点,即20m,这与负梯级先导长度是比较接近的。另外,本文在计算通道分形维数时也发现,闪电通道的弯曲程度随高度减小,如图4所示(网格步长取20m)。可能是由于地表面附近高大建筑物、高压线和树等尖端产生了大量电晕离子,使得近地面空间电势分布变得复杂,先导通道的弯曲程度在接近地面时增加。

利用上述数盒子方法,本文对青海和广东23次自然闪电通道的分形维数进行了计算。从工程应用的角度,而不是严格的数学证明,计算结果表明闪电通道是分形的,其分形维数为1.1～1.3,平均为1.2。

2.2 分形闪电通道的模拟

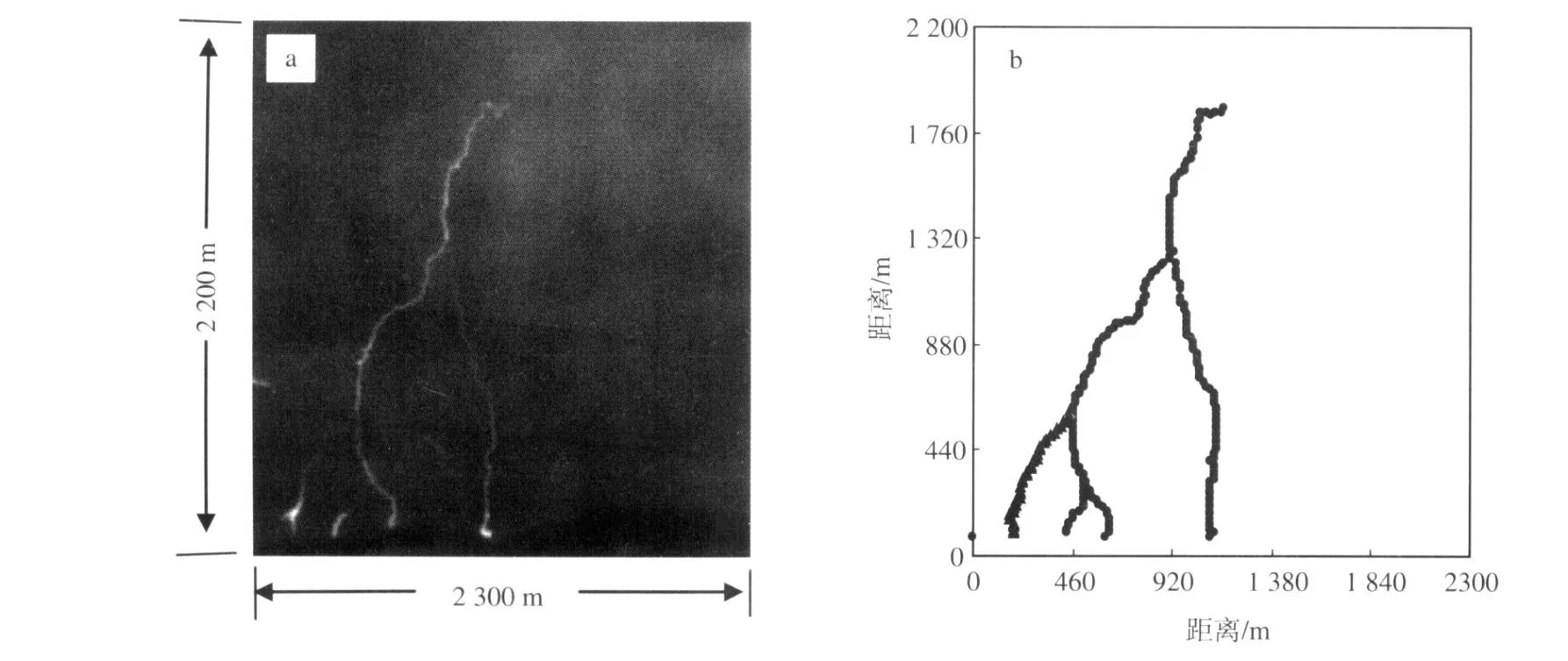
图2 利用高速摄像拍摄的实际闪电通道(a:高速摄像的照片;b:经过图像处理后的结果)[9]Fig.2 The lightning channel observed with a high-speed digital image system(a:the photo;b:the channel)[9]

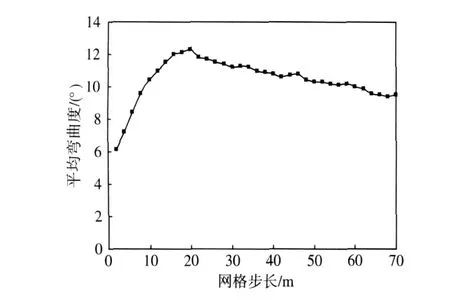
图3 闪电通道的弯曲程度随网格步长的变化Fig.3 Variation of the tortuosity of lightning channel versus the segment length

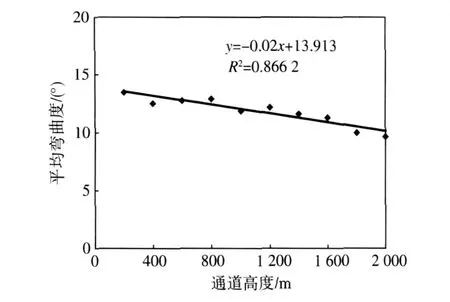
图4 闪电通道的弯曲程度随通道高度的变化Fig.4 Variation of the tortuosity of lightning channel versus the vertical channel height

分形闪电通道的模拟是对工程精度而言的,作为数学上的分形具有无限精细的自相似结构。工程上只要满足一定的精度,即可认为是分形的。本文假定闪电通道由N段方向任意、长度以一定概率分布的直线组成,模拟这样一种弯曲的具有分形特点的闪电通道一般采用中点置换法。中点置换法是借助布朗运动的增量具有相似性来实现分形闪道的。尽管这样的模拟方法缺乏微观的物理根据,但从宏观上看,由于雷暴天气系统过境时,空间电标势的分布具有很大的时变特征,使得沿电势梯度方向发展的先导通道与满足一定分形维数的布朗运动之间具有很大的相似性。根据2.1节确定的闪电通道的分形维数,图5是利用中点置换法模拟的一次三维闪电通道,以及在x-z和y-z平面的投影,二维分形维数分别为1.20和1.15。

3 分形闪电通道电磁场的数值模拟

为了模拟分形闪电通道电磁辐射特征,本文采用M TLL回击电流模式来模拟回击电流沿通道的时空分布。不过,考虑到通道的任意弯曲特点,M TLL模式可写为

其中:l′(S)为观测点t时刻看到的通道长度(如图1所示);Ltot为通道总长度。而通道底部电流用Heidler函数来表达

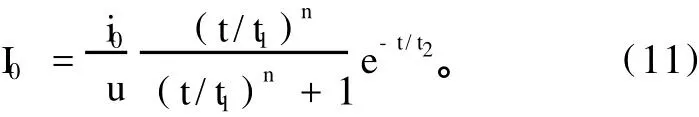
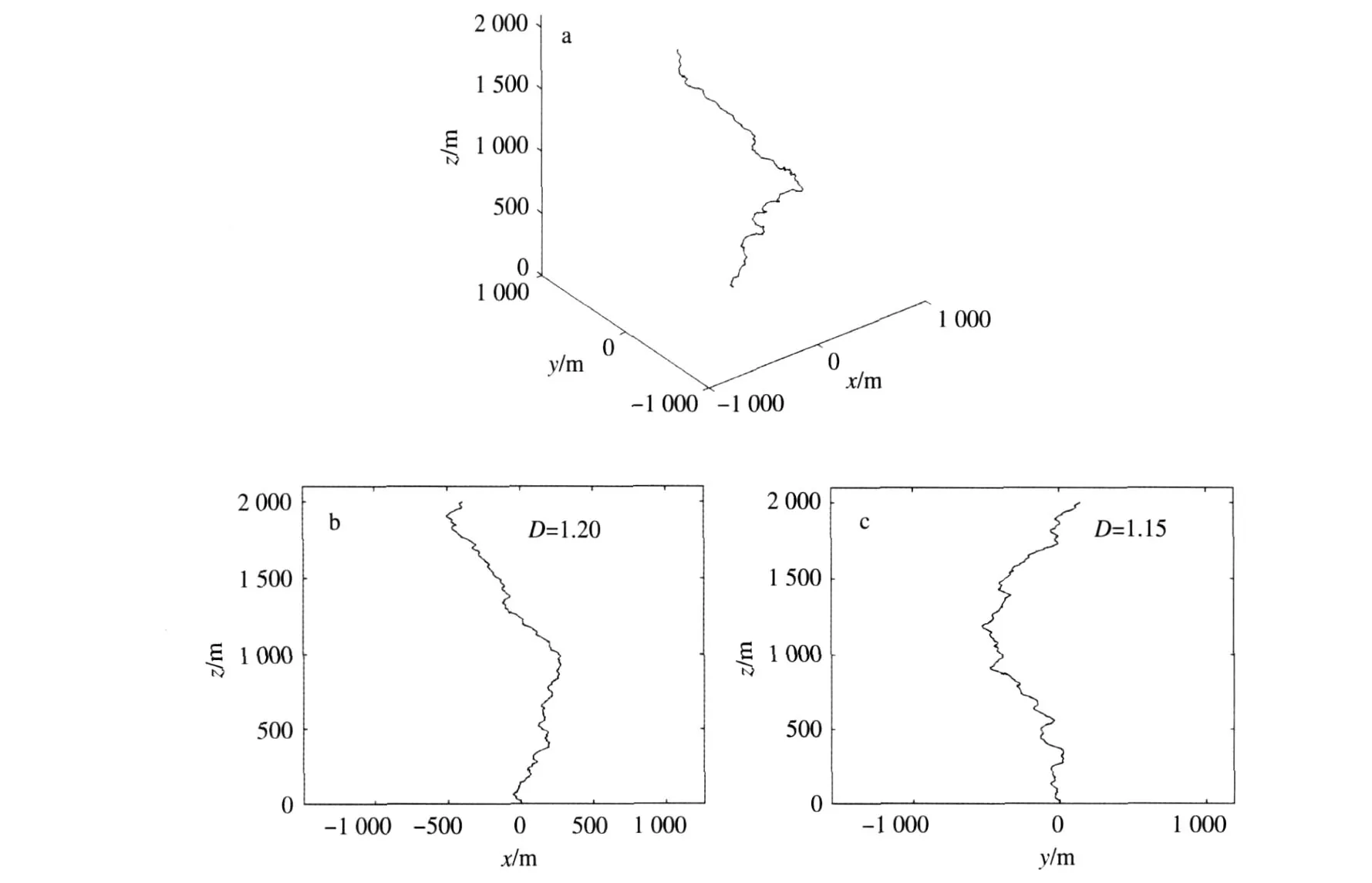
图5 利用中点置换法模拟的三维闪电通道(a)及其在x-z(b)和y-z(c)平面的投影Fig.5 Lightning channel simulation on(b)the x-z and(c)y-z plane and(a)its3-dimensional representation

其中:i0为雷电流峰值;u为电流峰值的修正因子;τ1决定波形的上升时间,τ2决定波形的下降时间。图6是通道底部输入的电流波形,具体参数如下:Cn=13kA,η=0.73,t1=0.15μs,t2=3μs,n=2。

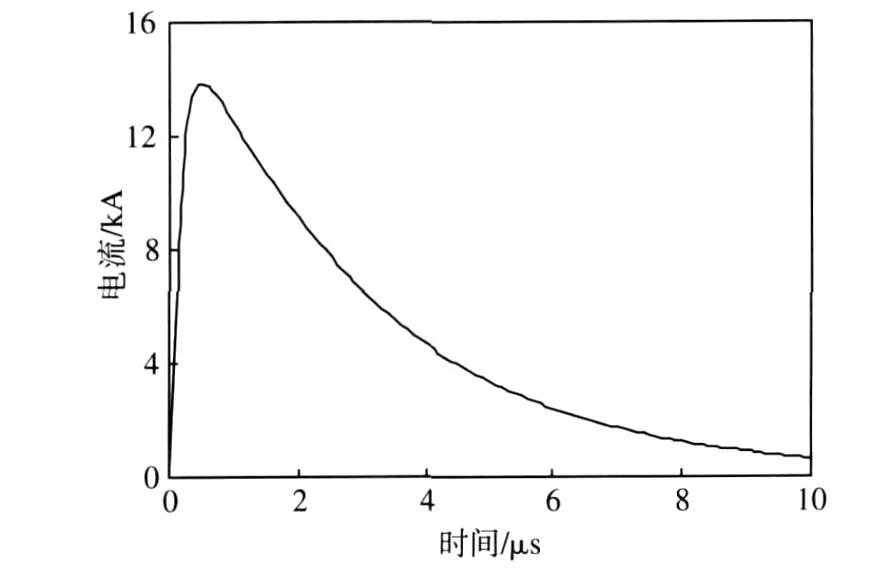
图6 通道底部的回击电流波形Fig.6 Return stroke current wave form at the lightning channel base

根据(8)和(10)式,可计算分形通道在地面不同距离、不同方位处产生的回击电磁场。假定地表面无限光滑、电导率无限大,图7和8分别给出了在地表面100m和100km处的时域垂直电场Ez和水平磁场变化波形,而每个距离分别给出了8个不同方位的回击电磁场变化。

从图7看出,距闪电通道100m处不同方位的回击垂直电场变化波形具有一定的相似性,但电磁场峰值强度随方位角的变化非常明显。这是因为当距离较近时(如图1所示),矢量R和dl′之间的夹角随方位角变化明显,而当距离较远时,二者夹角随方位角的差别逐渐消失。如方位角φ=5π/4垂直电场峰值强度是φ=π/4处的2.3倍(图7a)。与电场波形相比,回击磁场波形表现为丰富的高频振荡,其随方位角的变化也非常明显,φ=3π/2处的磁场峰值是φ=2π处的3.9倍。由此可见,忽视通道的弯曲,利用地面回击电磁场的测量结果反演回击电流峰值时可能会带来不小的误差。从图7b的计算结果看出,如果利用安培环路定律反演回击电流峰值时,由于测站位置的不同,反演的回击电流峰值相差2～4倍。

从图8看出,随距离的增加,不同方位回击垂直电场的差异逐渐减弱,但与100m处的电场相比,高频分量明显增加。其中,100m～10km之间,不同方位回击垂直电场比值介于0.8～2.3之间,因此,在不同方位利用传输线模式反演的回击电流峰值之比也为0.8～2.3。另外,通过对比发现,地面回击电磁场变化波形与通道回击电流波形差异较大,从地面电磁场变化很难获得回击电流波形等特征参量,这与Lupo等[7]的研究结果是相同的。不过,改变回击通道的分形维数,即改变通道的弯曲程度,相应的回击电磁场波形的分形维数也改变。从工程应用的角度,回击通道的分形维数与回击电磁场波形的分形维数是一致的。

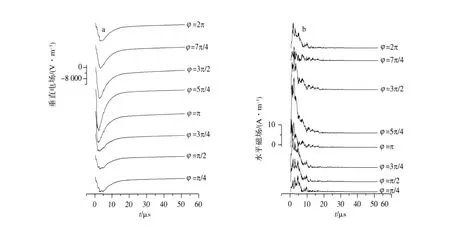
图7 在距闪电通道底部100m不同方位的电磁场 a.垂直电场Ez;b.水平磁场Fig.7 Wave forms of(a)z-component of electric field and(b)amplitudeof magnetic field in different azimuths at 100m from the channel

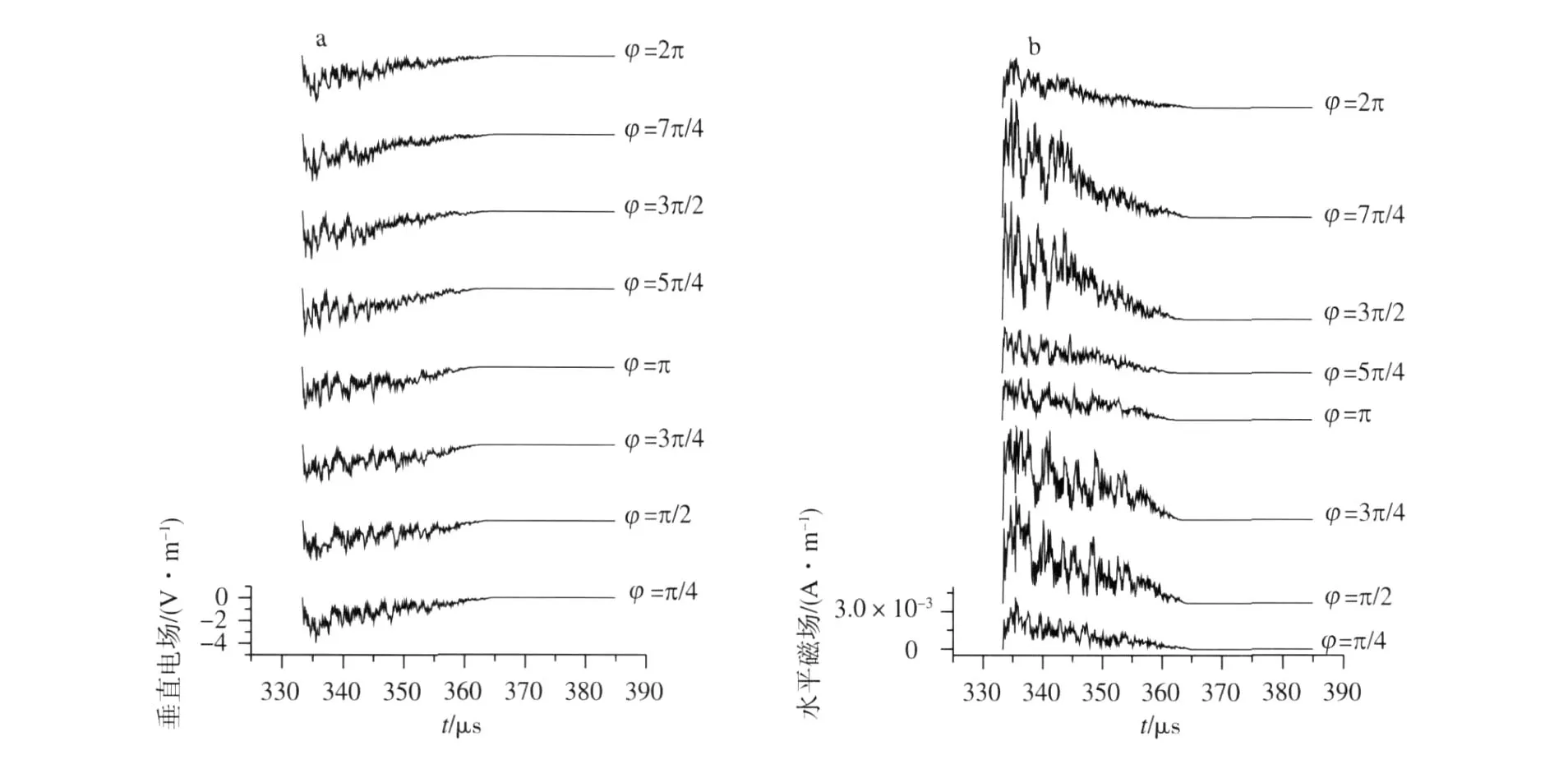
图8 在距闪电通道底部100km不同方位的电磁场 a.垂直电场Ez;b.水平磁场Fig.8 Waveform s of(a)z-component of electric field and(b)amplitudeof magnetic field in different azimuths at100km from the channel

4 结论与讨论

利用分形理论和偶极子辐射理论,研究了闪电通道的弯曲对电磁场计算的影响。结果表明,当观测距离较近时,由于闪电通道的弯曲效应,不同方位的回击垂直电场峰值差异较大;而当距离增加时,这种差别逐渐消失。但无论距离远近,地面水平磁场随方位角都存在较明显的差异。另外,与垂直通道的回击模式相比,考虑通道弯曲计算的回击磁场偏大2～4倍,且具有明显的高频分量,持续时间30μs左右,这些亚微秒量级的电磁辐射精细结构是研究雷电电磁感应的主要参量。因此,无论从回击电流的反演估算,还是计算雷电电磁感应,通道的弯曲效应都是不可忽视的。

另外,通过对比发现,如果假定通道笔直且垂直于地面以及电导率无限大,通道底部的回击电流波形与不同距离电磁场波形具有很好的一致性,尤其是初始上升沿部分保持相似[10]。但如果考虑通道弯曲(实际情况也是这样的),计算的不同距离处的电磁场波形与通道底部的电流波形差异较大,利用地面电磁场的测量结果很难获得闪电通道电流的某些参数,闪电通道底部的电流波形与电磁场波形之间缺乏明显的一致性。不过,通道弯曲程度和相应的电磁场波形的分形维数比较一致,可以利用地面电磁场波形的观测结果反演通道弯曲,建立相应的分形闪电模型,研究雷电电磁辐射以及与高压输电线之间的耦合机制等方面具有积极的意义。

[1] Hill R D.Analysis of irregular paths of lightning channels[J].J Geophys Res,1968,73(6):1897-1906.

[2] Hill R D.Electromagnetic radiation from erratic paths of lightning strokes[J].J Geophys Res,1969,74(8):1922-1929.

[3] LeV ine D M,M eneghini R.Simulation of radiation from lightning return stroke:the effects of tortuosity[J].Radio Science,1978,13(5):801-809.

[4] Vecchi G,Labate D,Canavero F.Fractal approach to lighting radiation on a tortuous channel[J].Radio Science,1994,29(4):691-704.

[5] Valdivia J A,M ilikh G,Papadopoulos K.L ightning as a fractal antenna[J].Geophys Res Lett,1997,24(24):3169-3172.

[6] 祝宝友,马明,陶善昌.地闪回击通道几何结构对VLF/VHF辐射场特征的影响[J].高原气象,2003,22(6):246-251.

[7] Lupo G,Petrarca C,TucciV,et al.EM fields associated with lightning channels:On the effect of tortuosity and branching[J].IEEE Trans Electromagnetic Compatibility,2002,42(6):394-404.

[8] Kawasaki Z,Matsuura K.Does a lightning channel show a fractal[J].Applied Energy,2000,67(9):147-158.

[9] 张其林.人工引发雷电流及其电磁辐射与传输特征的观测分析与理论研究[D].北京:中国科学院研究生院,2007.

[10] Wang D,Takagi N,L iu X,et al.Luminosity characteristics of multiple dart leader/return stroke sequences measured with a high-speed digital image system[J].Geophys Res Lett,2003,31(4):102-120.

Formulation of Fractal ChannelModel and Characteristics of Corresponding Electromagnetic Fields

ZHANG Qi-lin1,2,FENG Jian-wei1,2,ZHAO Zhong-kuo3,B IAN Jian-chun3

(1.KeyLaboratory ofMeteorologicalDisaster ofMinistry of Education,NU IST,Nanjing 210044,China;2.School ofAtmospheric Physics,NUIST,Nanjing 210044,China;3.Laboratory forMiddle Atmosphere and Global EnvironmentObservation(LAGEO),Institute ofAtmospheric Physics,Chinese Academy of Sciences,Beijing 100029,China)

Based on the lightning channel observed with a high-speed digital image system,the fractal lightning channel model is for mulated with the fractal method.In this paper,we analyse the effect of lightning channel tortuosity on the corresponding electromagnetic fields in different azimuths and different distances.The results show that,at close distances(100 m—10 km),the ratio of EF(electric field)peaks at any two azimuths is within 0.8—2.3.with the increase of distance,the dependence on azimuth weakens.However,the dependence of MF(magnetic field)wave for ms on azimuth is obvious,and the ratio of MF peaks at any two azimuths ranges about from 2 to 4.Compared with the return stroke model assuming a straight lightning of negligible cross section,the fractal channel model can well simulate the fine structure of the radiation fields,whose time-domain behavior exhibits a jagged shape with remarkable spectral content in several bands of fractal interest.

return stroke;channel tortuosity;fractal;vertical electric field;radiation field

P427.321

A

1674-7097(2010)06-0719-06

2010-01-07;改回日期:2010-04-20

国家自然科学基金资助项目(40975002);中国科学院知识创新工程领域前沿项目( IAP09313);江苏省高校自然科学基金资助项目(09KJB170005);公益性行业科研专项(GYHY200806014)

张其林(1971—),男,甘肃天水人,博士,副教授,研究方向为雷电物理、雷暴监测预警及雷害机理,qlzhang@nuist.edu.cn.

张其林,冯建伟,赵中阔,等.分形闪电通道模型的建立及其电磁辐射特征[J].大气科学学报,2010,33(6):719-724.ZhangQi-lin,Feng Jian-wei,Zhao Zhong-kuo,et al.For mulation of fractal channel model and characteristics of corresponding electromagnetic fields[J].Trans Atmos Sci,2010,33(6):719-724.

(责任编辑:倪东鸿)