地震作用下边坡稳定性分析①

范昭平，张丽华

（1.江苏省交通规划设计院，江苏南京 210005；2.南京工业大学力学部，江苏南京 210009）

地震作用下边坡稳定性分析①

范昭平1，张丽华2

（1.江苏省交通规划设计院，江苏南京 210005；2.南京工业大学力学部，江苏南京 210009）

考虑了边坡岩土体材料的动力特性以及地震特性，利用动力有限元时程分析方法对边坡在地震荷载作用下的动力特性进行了分析，采用最小平均系数对边坡稳定性进行了评价，并与拟静力法的结果进行了对比分析。对某工程实例计算结果表明该分析方法的可行性，可为地震作用下边坡工程设计工作提供一些有益的参考。

动力有限元；时程分析；稳定系数；拟静力法

Abstract：Dynamic fininte element method and time history analysis are explored to analyze dynamic property of slope during seismic process considering soil dynamic property and seismic characters.The minimum mean safety factor is explored to evaluate slope stability.The result is compared with the one of the pseu－static method.The result from a typical slope in a real case indicates that the method is feasible.

Key words：Dynamic FEM；Time history analysis；Safety factor；Pseudo－static method

0 引言

中国是一个多山的国家，山地面积约占国土面积的三分之二，这就从客观上决定了我国有大量的自然边坡。同时我国当前正处于经济飞速发展的时期，大量的基础设施建设，特别是西部大开发使我们面临大量的复杂人工边坡问题［1－3］。同时中国又是一个地震多发的国家，而西部地区是我国主要的强震区，地震的强度和发震频度都很高。据中国地震局统计，我国近代82%的强震都发生在西部地区。我国每年因地震而导致的滑坡灾害非常严重，特别是在山区和丘陵地带，地震诱发的边坡滑动和坍塌往往分布广、数量多、危害大。因此地震荷载作用下边坡的安全性将是工程建设中面临的难点问题［4－5］。

一般认为，地震荷载对边坡稳定性影响的主要原因是由于地震惯性力导致边坡整体下滑力加大，降低边坡的系数从而导致边坡失稳。目前地震作用下的边坡稳定系数的计算大多采用拟静力法和有限单元法［6－8］。拟静力法的基本假设就是认为地震过程中边坡一直受到水平向加速度的作用，而且作用方向不变。事实上这种作用不论在方向和数值大小上时刻都在变化，边坡的稳定系数为一时间函数，所以拟静力法所表达的地震作用的概念是不准确的。并且拟静力法即没有考虑地震的特性，如振动频率、次数和地震持续时间等因素，又没有考虑边坡岩土体材料的动力性质和阻尼性质等。因此拟静力法所得的稳定系数并不能说明边坡在地震荷载作用下的实际稳定性。

本文结合具体工程实例，考虑了边坡岩土体材料的动力特性以及地震特性，采用动力有限元时程分析方法对边坡在地震荷载作用下的动力特性进行分析，采用最小平均稳定系数对边坡稳定性进行评价并与拟静力法的结果进行对比分析。可为地震作用下边坡工程设计工作提供一些有益的参考。

1 计算方法

1.1 静力分析

应用静力有限元法计算边坡在地震前的初始静应力，目的是为边坡动力稳定分析提供初始应力条件。

1.2 动力分析

在边坡地震稳定分析时，土体动力平衡方程为

式中，［M］、［C］、［K］分别为计算模型的整体质量矩阵、整体阻尼矩阵和整体劲度矩阵｝、｛˙u｝、｛u｝分别是节点加速度、速度和位移列阵；｝是地震加速度列阵。整体阻尼矩阵由各个单元阻尼矩阵组成，单元阻尼矩阵［C］e采用瑞利阻尼，由下式计算

式中，系数αe＝λ，βe＝λe／，其中λe为单元阻尼比为土体振动基频。

对动力方程采用Wilson－θ法在时域内进行逐步积分求解，即可得到每一时刻所有节点动力反应值。

1.3 地震稳定性计算

动力抗滑稳定性分析在静力计算和动力计算的基础上进行。静力计算已得到各单元的σxs、σys、τxys，动力计算得到每个时刻的动应力σxd、σyd、τxyd，求出滑弧通过的各单元的滑面上的正应力σsi和剪应力τsi，动正应力σdi和动剪应力τdi，则滑弧上的正应力为σi＝σsi＋σdi，剪应力为τi＝τsi＋τdi。滑弧通过单元i的长度为li，该单元的抗剪强度为τfi，剪应力为τi，则整个滑面的抗滑稳定系数为

设边坡在静力作用下的稳定系数为Fs0，由于地震的作用，稳定系数随震动过程而波动，其最小的稳定系数为Fsmin。在地震作用下，边坡瞬间小于某一稳定系数不一定失稳，因此用最小稳定系数显然过于保守，而采用平均稳定系数又偏于危险，考虑到以上原因，有学者［9］建议取（Fs0－Fsmin）的0.65倍作为稳定系数的平均振幅来反映稳定系数因地震作用而偏离的幅度（参见图1），则最小平均稳定系数smin为

图1 最小平均稳定系数计算示意图Fig.1 Sketch of minimum average safety factor.

2 工程实例

2.1 工程概况

西藏藏东某滑坡位于川藏公路沿线，沿公路宽192m，垂直线路滑坡轴长90m，滑面为向公路倾斜的平面（图2）。滑坡体上部为残坡积碎石土，下伏基岩为泥质粉砂岩和泥岩。根据地质勘探情况，滑床表面较密实，滑带土为角砾土，覆盖层为坡残积碎石土。滑坡所在地区地处可可西里三江地震带，为Ⅶ度地震烈度区。由于该滑坡所处川藏公路的重要性，其地震稳定性需要进行专门的研究。

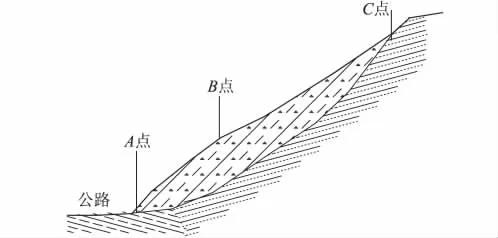
图2 工程实例边坡断面示意图Fig.2 Sketch of slope cross－section in a real case.

2.2 计算参数的选择

根据《中国地震动参数区划图》，滑坡区段设计峰值加速度为0.1g，反应谱特征周期为0.45s，竖向加速度分量取水平加速度分量的2／3。由于该地区缺乏相应的地震台阵记录资料，而通过现有的地震记录进行相应的调整是目前一种常用的方法。故本文考虑到当地的实际情况，通过调整具有一定代表性的EI－Centro波得到输入地震波，输入地震加速度时程曲线见图3。

根据勘察成果，并参考前人研究成果［10－12］，确定本次研究所需岩土体材料的力学参数（表1）。

图3 输入地震波加速度时程曲线Fig.3 Time－history curves of input seismic wave.

表1 边坡岩土体材料力学参数

2.3 计算结果

2.3.1 静力计算结果

利用静力有限元分析方法对边坡进行分析，得出最大竖向应力为1 651kPa，静力情况下边坡的稳定系数为1.270。

2.3.2 动力计算结果

采用动力有限元时程分析方法对边坡地震稳定性进行了计算，限于篇幅，本文仅给出边坡上典型几个代表性结点（参见图1：坡底A点，坡中B点，坡顶C点）的动正应力和动剪应力时程，计算结果如图4～图6所示。

2.3.3 地震稳定性计算结果

地震作用下边坡的稳定系数时程曲线如图7所示。边坡最小稳定系数其值为0.995，发生时间为2.32s。但考虑到最小稳定系数出现在某一瞬间时刻，在紧接着的下一时刻由于地震加速度的方向的改变稳定系数得到恢复。因此按最小平均稳定系数来评价边坡的地震稳定性，结果见表2。为了便于比较，本文给出了拟静力法的计算结果。从表中看出，采用本文方法计算所得的最小平均稳定系数为1.073，而采用拟静力方法计算所得的稳定系数为1.115，可见拟静力方法的计算结果与本文所计算的最小平均稳定系数并不完全一致，而且拟静力结果要比整个地震历时中的最小平均稳定系数大，这是因为拟静力法没有考虑到地震特性和土体的动力特性。

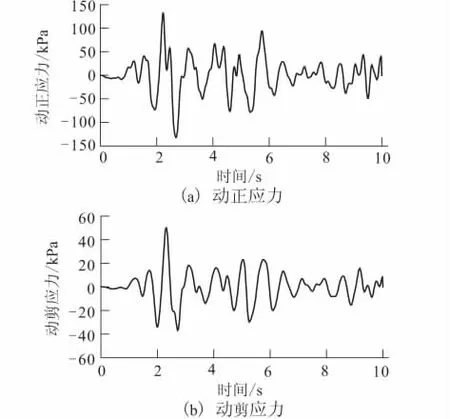
图4 坡底部结点A动应力时程曲线Fig.4 Time－history curves of node Aat slope foot.

图5 坡中部结点B动应力时程曲线Fig.5 Time－history curves of node Bat slope center.

表2 稳定系数计算结果

3 结论

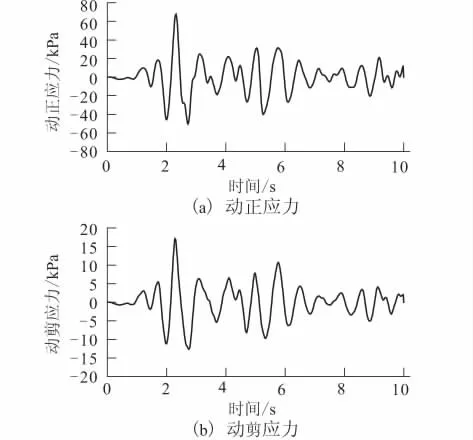
图6 坡上部结点C动应力时程曲线Fig.6 Time－history curves of node Con slope top.

图7 稳定系数时程曲线Fig.7 Time－history curve of safe factor.

本文考虑了边坡岩土体材料的动力特性以及地震特性，采用动力有限元时程分析方法对西藏某实际边坡在为Ⅶ度地震作用下的动力稳定性进行了分析，求得边坡地震时的动态稳定系数，在此基础上采用最小平均稳定系数对边坡稳定性进行评价，并与拟静力法的结果进行了对比分析，结果表明由于拟静力法由于没有考虑岩土材料的动力特性及地震加速度随时间变化等因素，从而稳定系数计算结果要比本文方法结果偏大。本文提出的方法可为地震作用下边坡工程设计工作提供一些有益的参考，但是，关于边坡地震稳定系数的取值标准，还有待于通过对大量边坡震害调查研究并进行校验和修正才能真正用于工程实际。

［1］ 陈祖煜.土质边坡稳定分析——原理·方法·程序［M］.北京：中国水利水电出版社，2003.

［2］ 姚艳华，彭刚，陈灯红.拟合水工设计反应谱的人工地震波的生成与Huang变换校正［J］.西北地震学报，2008，30（3）：255－ 260.

［3］ 郑颖人，陈祖煜.边坡与滑坡工程治理［M］.北京：人民交通出版社，2007.

［4］ 洪海春，徐卫亚.地震作用下岩质边坡稳定性分析综述［J］.岩石力学与工程学报，2005，24：4827－4836.

［5］ 赵要军，陈安.公共财政应急支持体系构建——以云南大姚地震为例［J］.西北地震学报，2008，30（2）：113－116.

［6］ 吴兆营，薄景山，刘红帅，等.岩体边坡地震稳定性动安全系数分析方法［J］.防灾减灾工程学报，2004，24（3）：237－241.

［7］ 吴兆营，景立平，薄景山.土石坝地震稳定性分析评述［J］.世界地震工程，2003，19（1）：44－50.

［8］ 尹紫红.地震作用下的滑坡稳定性分析［J］.铁道建筑，2007（9）：65－67.

［9］ 刘汉龙，费康，高玉峰.边坡地震稳定性时程分析方法［J］.岩土力学，2003，24（4）：553－556，560.

［10］ 水利水电科学研究院.岩石力学参考手册［M］.北京：水利电力出版社，1991.

［11］ 工程地质手册编委会.工程地质手册（第四版）［M］.北京：中国建筑工业出版社，2007.

［12］ 钱家欢，殷宗泽.土工原理与计算（第二版）［M］.北京：中国水利水电出版社，1996.

Analysis on Slope Stability during Earthquake

FAN Zhao－ping1，ZHANG Li－hua2
（1.Jiangsu Provincial Communication Planning ＆Desing Institute，Nanjing 210005；China；2.Mechanics Department，Nanjing University of Technology，Nanjing 210009；China）

TU435

A

1000－0844（2010）04－0339－04

2009－06－15

国家自然科学基金重大研究计划（90815020）

范昭平（1978－），男（汉族），陕西宝鸡人，博士生，注册土木（岩土）工程师，主要从事岩土工程的研究与设计工作.