气候变化对衢州水文站洪水频率分析的影响

徐 晓,林盛吉,张徐杰,张庆庆,许月萍

(浙江大学建筑工程学院,浙江杭州 310058)

近年来气候变化导致我国水资源年际间的丰枯交替频繁,年内洪涝、干旱灾害严重,空间分布不均加剧[1].全球气候变暖的同时,区域水循环形式发生变化,水循环周期变短,速度加快,该变化的一个重要表现就是降水的时空分布发生改变[2-3],导致干旱洪涝等极端事件时有发生.气候变化对人类生产生活的影响主要是通过极端事件发生频率和强度的变化,而不仅仅是平均气候状况的变化,因此,分析全球气候变化背景下流域水文特征值的改变有助于了解气候变化对干旱洪涝等灾害发生频率的影响,有很大的现实意义[4].

众多的影响因素造成了气候变化预测的复杂性,通常使用的气候模型的分辨率并不高,要对小流域进行准确预测是不现实的,而水文资料中存在大量时间序列数据,发现水文时间序列中蕴藏的规律,有利于掌握水文现象的变化规律和趋势[5],因此可以采取统计学的方法来研究小流域对气候变化的响应.本文选择衢州水文站为研究对象,使用线性矩方法对所选分布函数进行参数估计,采用30a滑动平均法分析气候变化对分布线型参数变化趋势的影响.

1 研究区域数据

1.1 异常值检验

衢州水文站属国家重点水文站,位于钱塘江上游,是兰江的控制水文站,控制流域面积为5424km2,流域属山地地形,多山溪河流,坡陡流急,容易诱发洪涝灾害.本文选用衢州水文站1947—2006年共60a的日流量数据,使用年最大值法从日流量数据中提取流量时间序列.先对流量时间序列进行异常值检验,异常值有可能是测量过程操作不规范造成的,或者资料整编中出现疏忽所致,异常值的存在会破坏样本序列的一致性,而水文过程是随机过程,一旦样本序列丧失了一致性,则不能直接用来进行频率分析.本文使用样本残差图对流量时间序列进行异常值检验,如图1所示.

从图1可以看出,流量时间序列均匀随机地分布在零线的两边,没有残差明显偏大或者偏小的异常值出现,其中1948年7月14日的残差值偏大,最大日流量达8510m3/s,查阅相关资料,该日附近几天有持续降雨过程,导致水文站测得的流量值很大,所以该流量值具有合理性,可以认为流量时间序列具有较好的一致性.

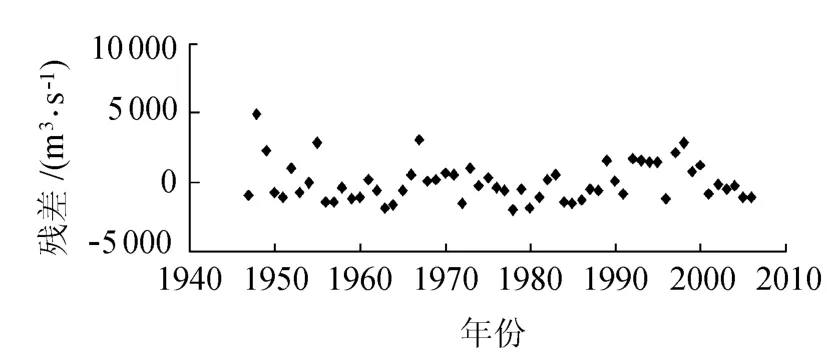
图1 流量时间序列残差Fig.1 Relation between residual and time series of discharge

1.2 趋势检验

对所选流量时间序列使用一阶线性回归拟合,如图2所示,可见60a间衢州水文站的流量数据有较大的波动,最大流量值(8510m3/s)是最小流量值(1240m3/s)的6.86倍;流量的年际变化很大,存在着明显的丰枯周期,较早年份流量数据的年际间的波动较大,丰枯年间的变化明显,而1973年之后流量数据波动的幅度较小,丰水年和枯水年的流量差别减小.总体来看,流量序列有减小的趋势.通过Mann-Kendall非参数检验法[6-8]进行趋势检验,结果表明该流量时间序列有微弱的下降趋势,但不明显.

上述流量数据的变化既有可能是气候变化引起的,比如全球变暖导致的降雨和蒸发量的变化,但也不排除人为因素,比如人类活动对流域下垫面的影响,影响了产流过程;从河流取水用于灌溉直接影响了流量;上游地区水库丰水期拦蓄水,枯水期放水,影响了自然的径流过程,使得丰枯流量的差别减小等等.为了进一步分析流量时间序列的趋势,现对频率分析分布曲线的参数趋势进行分析.

近年来,线性矩法(L-moments)已经被证明是一种非常有效的分布曲线参数估计方法,且被广泛地应用于洪水和枯水的频率分析中[9].本文使用线性矩方法估计分布曲线的参数,并分析参数的变化趋势.

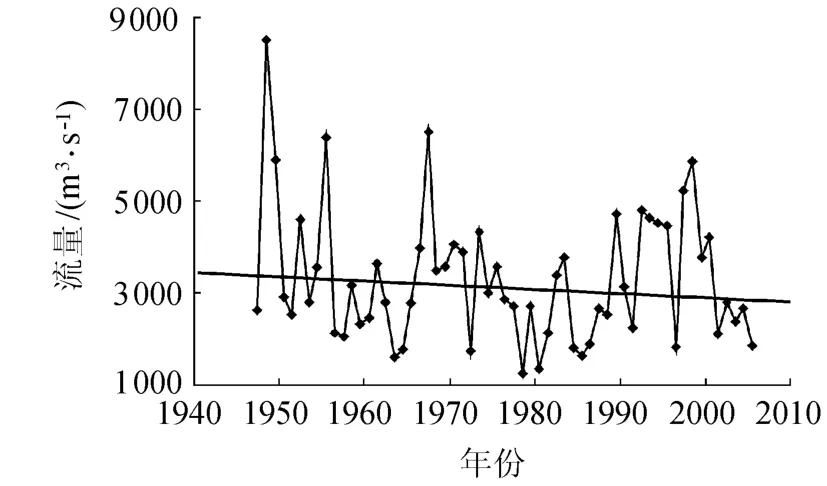
图2 衢州水文站流量时间序列及其趋势线Fig.2 Time series and trend of discharge at Quzhou hydrological station

2 研究方法

2.1 线性矩原理

线性矩来源于Greenwood等[10]提出的概率权重矩(PWM),随机变量X的第r+1阶线性矩为

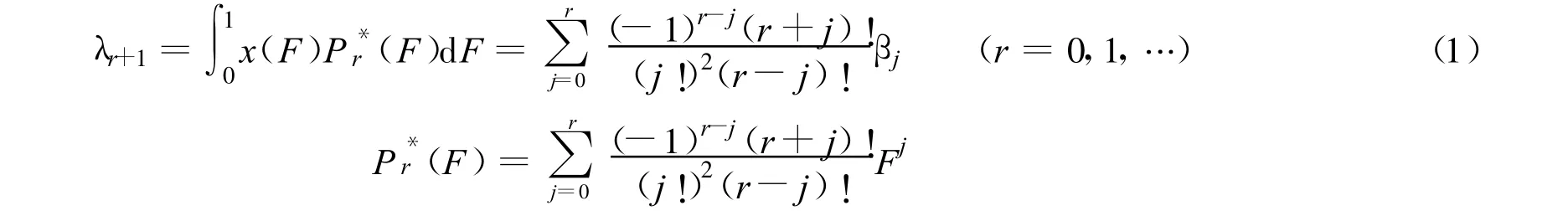
其中

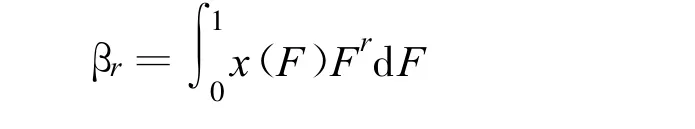
式中:F——随机变量X的累计分布函数;x(F)——累积分布函数F的反函数.利用水文时间序列来计算样本线性矩时,假设随机变量X有n个样本,按从小到大排序,即X 1/n≤X 2/n≤Xi/n…≤Xn/n(i=1,2,…,n),Xi/n为n个值中第i小的值.前 r+1阶样本线性矩定义[10-11]为

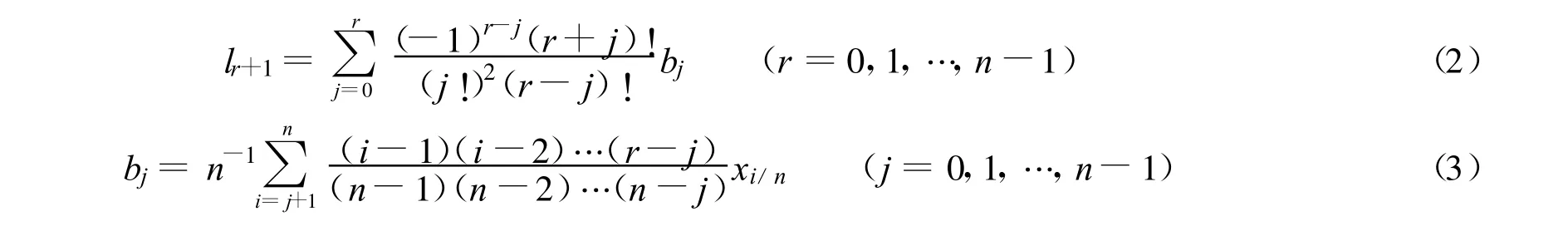
式中:bj——概率权重矩 βj的无偏估计值;t——样本离差系数,定义为 t=l2/l1;τ3,τ4——偏态系数和峰态系数,τ3,τ4通常写作 t3,t4,分别定义为 t3=l3/l2,t4=l4/l2.

2.2 分布曲线

本文采用广义极值分布(GEV分布)对流量时间序列进行拟合,广义极值分布的概率密度函数[12]为

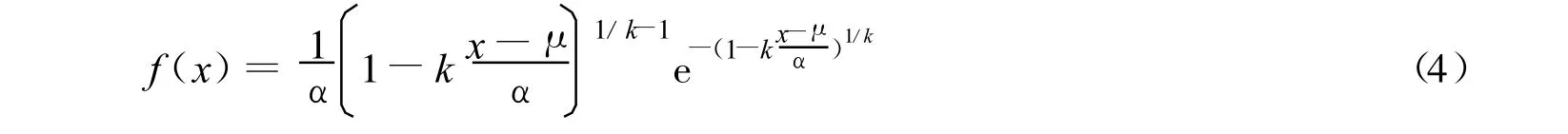
式中:μ——位置参数;k——形状参数;α——尺度参数.针对广义极值分布,重现期为 T时的设计洪水计算公式[12]为

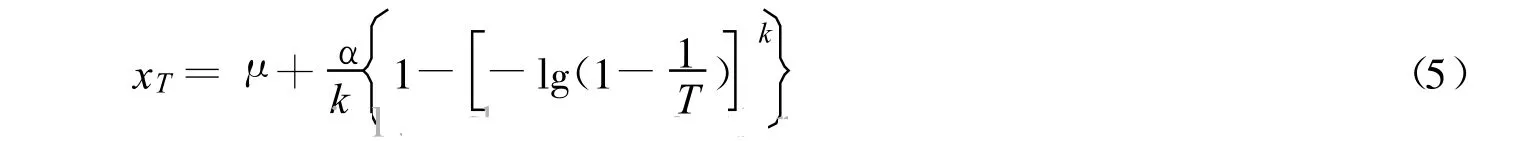
3 研究结果及分析

首先通过线性矩方法对前述3个参数进行估计,采用30a滑动平均法,即每30a作为一个数据样本,逐年依次向后推算,一直到第60年,共估计得到31组参数,如图3所示.

图3 广义极值分布参数变化趋势Fig.3 Trend of parameters of generalized extreme valuedistribution

从图3中3个参数的变化趋势可以得出以下结论:

a.随着时间的推移,广义极值分布的3个参数都存在明显的变化,变化率大小不等,因而根据相应参数计算的设计洪水值也会有相应的波动.

b.3个参数中,k即形状参数的变化趋势最明显,计算得到其变率为171%,形状参数影响的是分布函数的形状,形状参数越大,广义极值分布曲线越陡,同样的重现期,曲线越陡,设计洪水越小,因此形状参数反向影响设计洪水的大小.以第18个流量时间序列左右(1963—1992年)为分界,之前形状参数缓慢增加,之后以较大的斜率增大而后减小.

c.α即尺度参数的变率为24%,第18个流量时间序列之前的尺度参数变化平稳,之后则出现了较大的波动,同样存在先增大后减小的趋势.

d.μ即位置参数的变率为13.4%,波动最小,第18个流量时间序列之前减小,之后先增大后减小,3个参数发生明显变化的时间点是一致的,即k,α和μ在第18个时间序列左右同时突然增大,在第24个时间序列左右同时突然减小.

上述参数变化趋势表明选用不同的流量时间序列估计的参数有较大差异,从而导致最后计算的设计洪水也不一致,因此选择流量时间序列时要排除水文样本中的异常值,如果是径流资料,需要检验径流资料是否存在突变点,资料丧失一致性时要进行径流还原;从参数趋势可以看出气候变化对分布曲线参数的影响是比较明显的,而参数的趋势即反应了设计洪水的波动,间接说明了气候变化对设计洪水有较大影响.

4 结 语

愈演愈烈的气候变化,增加了极端天气发生的频率和强度,应对极端天气除了加强防范措施,还需要提高对极端天气的预测精度,洪水频率分析的任务即根据已有的水文数据序列预测洪水,数据序列长可以降低频率分析的不确定性,但是长数据序列难免会受到气候变化的影响,因此研究频率分析中分布曲线参数的变化趋势很有必要.本文通过研究衢州水文站的频率分析分布曲线参数的变化趋势来研究气候变化对频率分析精度的影响.结果表明气候变化对洪水频率分析有较大影响,因此在进行频率分析时应该充分考虑气候变化的影响,把水文时间序列分为自然的水文随机过程和气候变化下的非随机过程,以此提高设计洪水计算精度,为调水等工程的实施提供更有力的依据.

[1]李林,汪青春,张国胜,等.黄河上游气候变化对地表水的影响[J].地理学报,2004,59(5):716-722.(LI Lin,WANG Qingchun,ZHANG Guo-sheng,et al.The Influence of climate change on surface water in the upper Yellow River[J].Acta Geographica Sinica,2004,59(5):716-722.(in Chinese))

[2]褚健婷,夏军,许崇育,等.海河流域气象和水文降水资料对比分析及时空变异[J].地理学报,2009,64(9):1084-1092.(CHU Jian-ting,XIA Jun,XU Chong-yu,et al.Comparison and spatial-temporal variability of daily precipitation dataof weather stations and rain gauges in Haihe River basin[J].Acta Geographica Sinica,2009,64(9):1084-1092.(in Chinese))

[4]詹道江,叶守泽.工程水文学[M].北京:中国水利水电出版社,2000.

[5]张建云,章四龙,王金星,等.近50年来中国六大流域年际径流变化趋势研究[J].水科学进展,2007,18(2):230-234.(ZHANG Jian-yun,ZHANG Si-long,WANGJin-xing,et al.Study on runoff trends of the six larger basins in Chinaover the past 50years[J].Advances in Water Science,2007,18(2):230-234.(in Chinese))

[6]丁晶,邓育仁.随机水文学[M].成都:成都科技大学出版社,1988:1-121.

[7]MANNH B.Nonparametric tests against trend[J].Econometic,1945(13):245-259.

[8]VAN B G,HUGHES JP.Nonparametric tests for trend in water quality[J].Water Resources Research,1984,20(1):127-136.

[9]黄国如,陈永勤,解河海.东江流域枯水径流的频率分析[J].清华大学学报:自然科学版,2005,45(12):1933-1935.(HUANG Guo-ru,CHEN Yong-qin,XIE He-hai.Low flow frequency analysis in Dongjiang basin[J].Journal of Tsinghua University:Science and Technology,2005,45(12):1933-1935.(in Chinese))

[10]GREENWOOD J A,LANDWEHR J M,MATALAS N C,et al.Probability weighted moments:definition and relation to parameters of several distributions expressable in inverse form[J].Water Resources Research,1979,15(5):1049-1054.

[11]HOSKING J RM,WALLISJ R.Regional frequency analysis an approach based on L-moments[M].New York:Cambridge University Press,1997.

[12]RAO RA,HAMEDK H.Flood frequency analysis[M].Boca Raton,Florida:United States of America CRCPress,2000.