岩体渗流的一种改进数学模型

张文捷,程荣兰,詹美礼,盛金昌,王国进

(1.河海大学水利水电工程学院,江苏 南京 210098;2.江西省水利厅,江西 南昌 330009;3.云南省电力设计院,云南 昆明 650051;4.昆明勘测设计研究院,云南 昆明 650051)

岩体渗流是影响高坝等工程安全的关键要素之一.岩体渗流不同于多孔介质渗流[1-7],岩体由裂隙和被裂隙切割的岩块构成,岩块的渗透性极弱,裂隙的渗透性极强,裂隙渗流不服从达西定律.国内外众多学者对岩体渗流进行了大量的研究,虽然在理论和数值模拟方面取得了许多成果,但是岩体渗流研究理论还不十分成熟.常用的数学模型主要有4种:等效连续介质模型[8-9];离散裂隙网络模型[10];双重介质模型(或多重介质模型)[11];离散-连续耦合模型[12].这4种模型的不足之处是:(a)拟真性较差.离散裂隙网络模型中裂隙分布的离散、无规律性决定了目前探测技术无法较完全地统计出计算所需的所有裂隙集合产状,故使得数学模型拟真性降低;连续介质模型不考虑裂隙与孔隙之间的水交换,将裂隙岩体也作为连续介质处理,裂隙中的水流量被等效平均到整个岩体中,故该模型拟真性也较差.(b)水量交换项难以确定(如离散裂隙网络模型、双重介质模型和离散-连续耦合模型).(c)无法反映岩体中真实存在的水头间断现象,更无法定量反映出水头间断程度.

为了探求一种合理反映岩体渗流的数学模型,本文从裂隙岩体离散-连续介质渗流机理出发,在2种强弱透水接触面上引入无厚度虚拟渗透突变单元(或称水头突变单元),根据强弱透水介质接触面处节点流量相等建立改进的离散-连续介质耦合模型,提出了反映水头间断程度的连续系数概念,并分析了合理的连续系数取值规律.

1 三维渗透突变单元有限元模型

1.1 渗透突变单元在岩体渗流数值模拟中的意义

在裂隙岩体渗流中,岩体块体渗透性很小,基本只起储水作用,裂隙是岩体的主要透水通道.在强导水的大裂隙壁面附近往往有很大的水头跌落,形成较大的水头间断.

为了真实地反映岩体中渗流场分布的间断突变性,本文借鉴位移突变单元的思想.这既能够解决连续介质模型中忽略岩块与裂隙之间的水量交换的不足,又能够弥补双重介质模型中水量交换量难确定的缺陷,可以比离散网络模型更能够高效、真实地模拟岩体渗流.引入渗透突变单元的基本思想是:在主干裂隙离散域(或断层破碎带)与岩体域接触面上加入8节点无厚度虚拟单元.鉴于此无厚度单元在岩体渗流模拟中的意义,本文称其为渗透突变单元.渗透突变单元是常规有限元的一种特殊单元模式.用渗透突变单元模拟水头间断,其前提条件是不改变整体渗流场流量,在等效节点流量相等原则下,通过在2种介质接触面上引入渗透突变单元来实现岩块与裂隙(断层)之间的水量交换,并模拟2种介质交界面处水头突变现象.

1.2 三维渗透突变单元计算理论与渗透机理分析

本文借鉴非连续变形Goodman接触面的处理方式,在裂隙和岩体的交界面上引入渗透突变单元.该单元为8节点无厚度单元(图1),其法向厚度为0,故只考虑法向渗透性,而忽略切向渗透性.

从数学间断角度出发,图1中渗透突变单元左侧面节点物理量 Φ-和右侧面对应节点物理量 Φ+不相等,即体现为同一点上物理量间断不连续.引入具体的渗流场分析,渗透突变单元左右侧面上的不连续的物理量即为水头H.在流量连续原则上,保证不改变整体渗流场流量,将图1中的渗透突变单元运用到渗流分析中,当渗透突变单元完全不透水时,在渗透突变单元左、右侧面上水头绝对间断;随着渗透突变单元不同程度破损,水头间断程度随之减小,当达到一定破损度后,渗透突变单元失效,左右两侧水头值大致相等.

根据有限元基本理论,引入插值函数Ni,构造函数,令Mi=-Ni,Mi+4=-Ni+4,i=1,2,3,4,得到单元内各节点的水头差

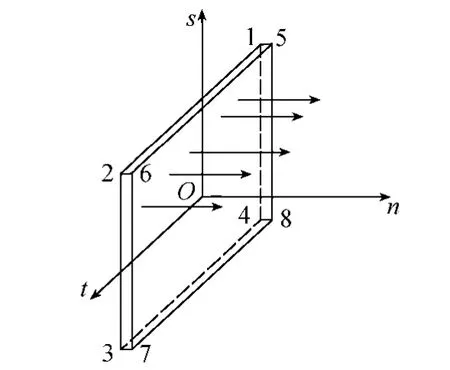
图1 无厚度渗透突变单元Fig.1 Discontinuous element with zero thickness

式中:ΔH——水头差;H+,H-——渗透突变单元左、右侧面的分布水头;Hi——i节点水头.

渗透突变单元法向厚度为0,故只考虑法向渗透性.借鉴土工膜防水性能优劣判别思想[13],即当防渗土工膜的厚度比较小时,无法仅从渗透系数来衡量透水性,故将渗透系数和薄膜厚度一起考虑,常用透水率来衡量土工膜的防水优劣程度.由于本文引入的渗透突变单元是一种虚拟的无厚度单元,故此也用虚拟渗透率来衡量渗透突变单元渗透性强弱.根据达西定律,当L=0时,流速只与虚拟渗透系数和渗透突变单元的水头差有关,即

式中:V——渗透流速;Kn——渗透突变单元的法向虚拟渗透率.

改进模型的等效节点流量表达式为

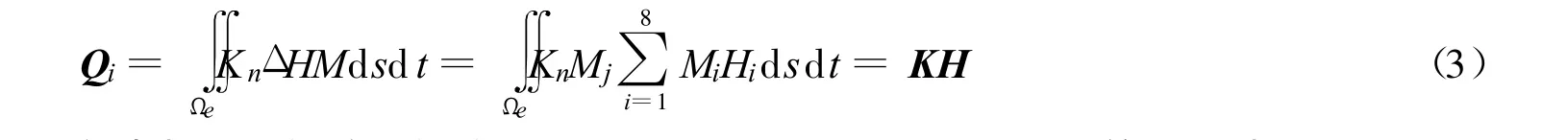
式中:K——渗透突变单元局部坐标系下的渗透矩阵;Qi——节点 i处的流量;Ωe——单元区域;s,t,n——3个方向的坐标.

渗透突变单元在本文数学模型中的作用之一是通过调整渗透率来恰当反映不同程度的水头突变间断现象,故结合间断系数的数学、物理意义及在本文数学模型中的作用,这里将渗透突变单元虚拟渗透率Kn定义为连续系数.Kn的合理取值是水量交换模拟合理正确的关键,也是正确反映水头间断程度的关键因素.

上述推导是在局部坐标系下进行的,为了集成整体渗透矩阵,需要将局部坐标转化为整体坐标.最终得到的整体坐标下的节点水头与节点流量关系式为

2 算 例

选择一理想的水文地质体进行研究.模型尺寸长×宽×高为100m×50m×50m,三维计算网格如图2所示.沿地质体长度方向(x方向)取左侧的50m为弱透水介质,右侧50m为强透水破碎带.在强弱透水介质接触面x=50m的位置加入渗透突变单元.根据计算需求,对模型网格局部加密剖分,模型共划分为20400个单元,块体单元20000个,渗透突变单元400个,节点22932个.边界条件:上、下游水位分别为49m和5m,两者作为已知水头边界(图3),位于下游水位以上的右侧面边界,视为可能出渗边界.

图2 渗流场计算网格模型Fig.2 Meshes for calculation of seepage field

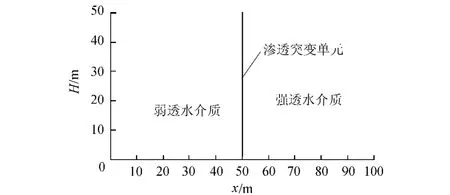
图3 透水介质分布和边界条件Fig.3 Distribution of permeable media and boundary conditions

2.1 模型验证

拟定弱透水介质的渗透系数K弱为1.0×10-6cm/s,强透水介质的渗透系数K强为1.0×10-2cm/s.本文数学模型的验证通过与常规数学模型计算结果的对比来实现.

a.渗流场计算结果比较分析.沿 x方向取一典型剖面,将常规数学模型与本文数学模型计算得到的渗流场等值线以及侵润面绘于同一张图上,如图4所示.从图4可以看出,常规数学模型基本能反映该岩体中的渗流场分布,但是,在强弱透水介质的接触面(x=50m)处,水头未在此处急剧下跌,而是在接触面左侧3～5m范围内缓慢降低,如浸润线AB段,浸润面凹至弱透水介质中,这是计算的不合理之处,且从计算结果来看,常规数学模型未能反映强弱透水接触面处的水头突变现象.运用本文改进的离散-连续介质耦合模型,通过调整连续系数取值,使得浸润线从强弱透水介质接触面位置C点跌至B点,形成急剧变化的水头间断.从水头间断吻合度来看,BC段能较好地反映此水文地质体中接触面处的水头间断现象.

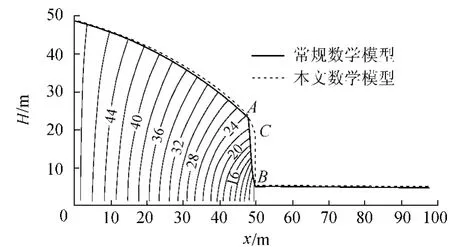
图4 渗流场等值线及侵润面计算结果比较Fig.4 Comparison of contours and phreatic faces of seepage field of conventional and proposed models

b.流量分析.在x=10m处截取一剖面,常规数学模型得到的流量为2.02m3/d,而本文数学模型得到的流量为1.90m3/d,2种模型的流量仅相差5.4%.这表明,渗透突变单元没有改变整体渗流量,渗透突变单元模型是正确的.

上述分析表明,改进的离散-连续介质耦合模型能反映复杂岩体结构中的渗流场分布,可以通过改变渗透突变单元连续系数来控制水量交换,比双重介质模型确定水量交换项要快捷,且有常规数学模型流量和水头间断程度作为连续系数取值衡量指标,确保了水量交换的模拟正确性.此外,由于渗透突变单元特殊的单元性质,通过合理的连续系数取值,渗透突变单元又能定性、定量地反映出强弱透水介质接触面上的水头突变间断程度,这一点也是几种常规数学模型无法模拟的.

2.2 水头间断程度与连续系数取值规律

2.2.1 K强/K弱=10000时

强弱透水介质渗透系数取值分别为1.0×10-2cm/s和1.0×10-6cm/s,在x=10m处截取一平面,分别计算有无渗透突变单元时通过该截面的流量,统计结果见表1,渗流场分布如图5示.

从图5可以看出:当Kn=1.0×10-9s-1时,渗透突变单元相当于不透水,起到很大的阻水作用,渗流场与加入渗透突变单元前反映的渗流场严重不符;当Kn=1.0×10-7s-1时,浸润线4的 CB段能解决AB段倾入弱透水介质中的不合理之处,同时,水头在CB段陡然下跌,反映了水在2种渗透性差异大的介质交界面水头不连续现象;当Kn=1.0×10-5s-1时,渗透突变单元的作用已体现不出.因此,Kn=1.0×10-7s-1,即小于K弱的1个数量级时,改进的离散-连续介质耦合模型能合理反映K强/K弱=10000时的水头间断规律.

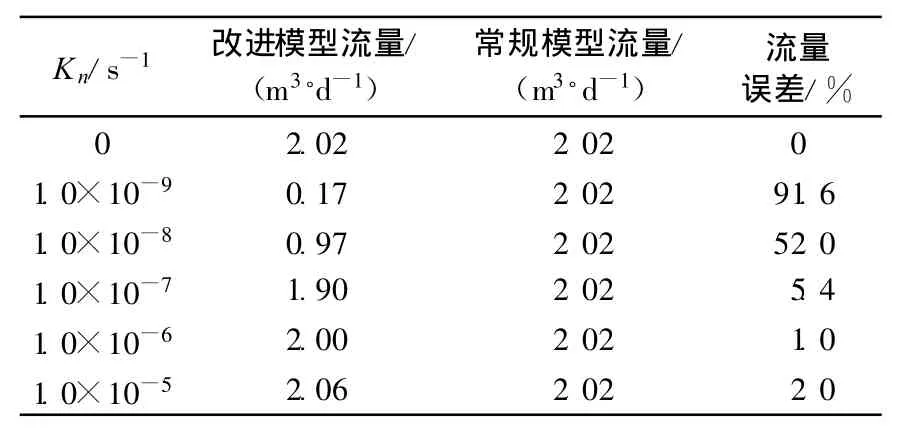
表1 不同Kn时加渗透突变单元前、后断面流量比较Table1 Comparison of flux amounts with and without discontinuous elements with different Kn

从流量可以看出:当Kn=1.0×10-9s-1时,有无渗透突变单元时通过断面的流量相差近92%,此时完全不符合不改变整体渗流场流量的条件;当Kn=1.0×10-7s-1时,二者流量仅相差5.4%;当Kn=1.0×10-6s-1时,可看作突变单元大部分破损,此时通过断面流量基本等于加渗透突变单元前流量.这表明,当Kn取小于K弱1个数量级时,渗流场计算结果合理.由此可见,在K强/K弱=10000,且Kn小于K弱的1个数量级的条件下,改进的离散-连续介质耦合模型能合理反映渗流场水头间断现象.

2.2.2 K强/K弱=1000,500,100,50,10时

K弱=1.0×10-6cm/s,K强根据不同要求相应改变.各种连续系数取值条件下的渗流等值线如图6和图7所示.从流量和渗流场的比较可以看出:当K强/K弱=1000时,Kn的合理取值范围是1.0×10-7s-1≤Kn≤3.0×10-7s-1;当K强/K弱=500,100,50时,Kn均取K弱数量级的0.3～0.5倍,即在本例中取 3.0×10-7s-1≤Kn≤5.0×10-7s-1;当K强/K弱=10时,Kn和K弱为同一个数量级,即在本例中取Kn=1.0×10-6s-1.

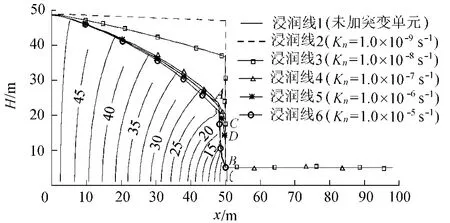
图5 K强=10000K弱条件下的渗流场等值线Fig.5 Contours of seepage field when K强=10000K弱

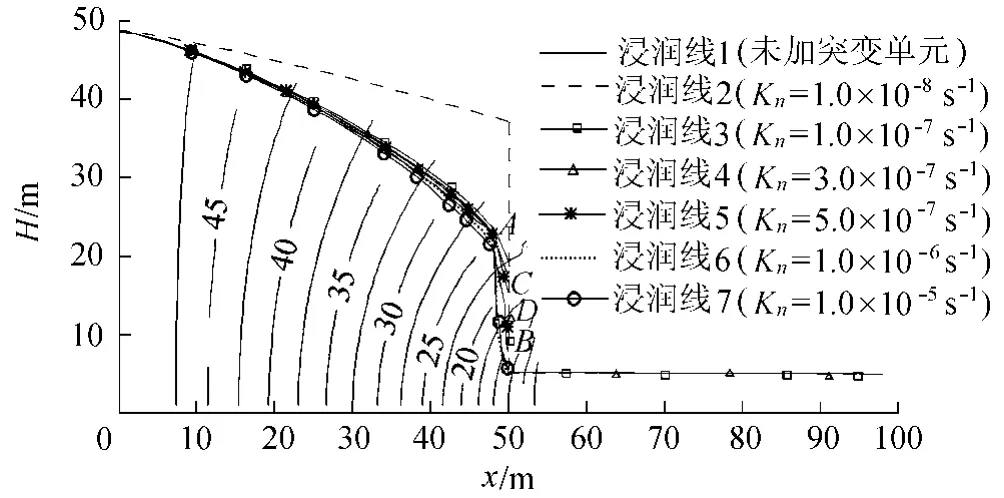
图6 K强=1000K弱条件下的渗流场等值线Fig.6 Contours of seepage field when K强=1000K弱

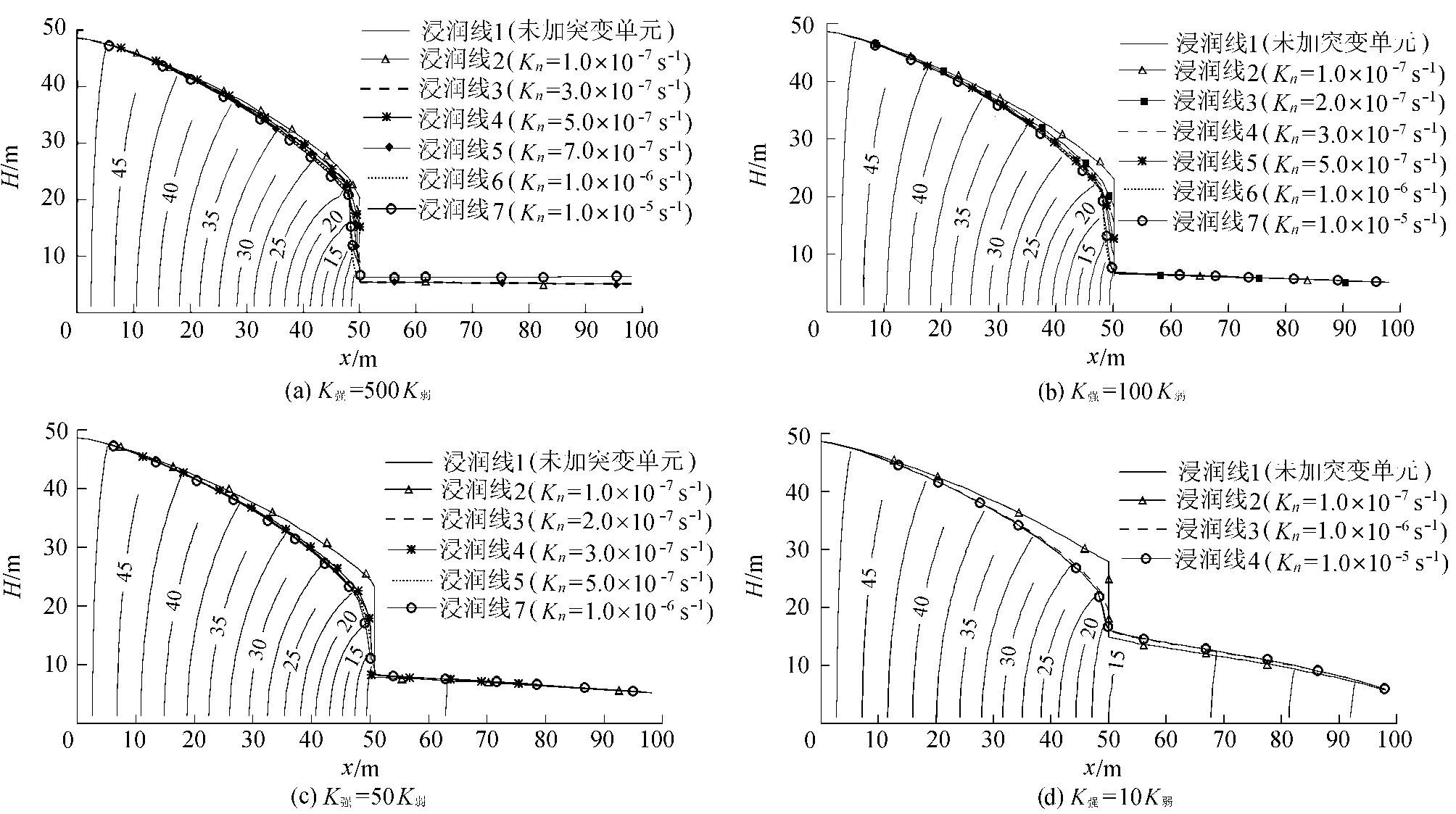
图7 不同K强/K弱条件下的渗流场等值线Fig.7 Contours of seepage field with different cases of K强/K弱

2.3 连续系数取值规律

取K弱的数量级为m,突变单元的渗透性量级为n;n=m/10,即n小于m 1个数量级.通过对强、弱透水介质渗透性不同差异倍比条件下多组合计算分析,得出水头突变单元连续系数Kn取值大小和突变介质渗透性倍比之间的关系,如表2所示.

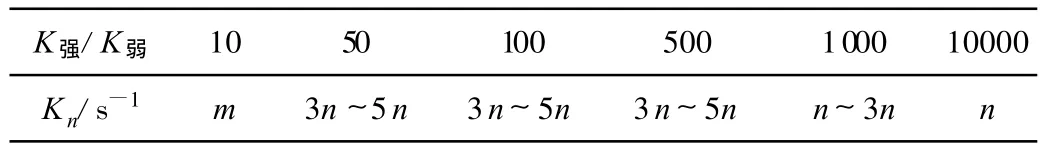
表2 突变介质渗透性倍比与水头突变单元连续系数关系Table2 Relationship between permeability ratio of discontinuous media and continuous coefficient of head discontinuous elements

3 结 语

本文从离散-连续介质渗透机理出发,在接触面处引入无厚度渗透突变单元,通过这种特殊模式的单元与常规单元的耦合,改进和完善了常规岩体渗流数学模型,改进后的岩体渗流数学模型(称为改进数学模型)可以更加真实地反映岩体渗流特性;采用常规数学模型和改进数学模型对同一地质体进行了渗流计算,计算结果验证了改进数学模型的正确性和合理性;提出了反映水头间断程度的连续系数概念,通过不断调整渗透突变单元连续系数,能较容易地解决常规数学模型中水量交换难确定的问题;在不改变整体渗流场流量的前提下,用不同水文地质条件下的水头间断程度作为衡量指标,总结出了能恰当反映不同间断程度的水头间断现象对应的连续系数取值规律,为渗透突变有限元中单元间断强弱参数的选取提供了具体确定的物理背景、方法和取值依据.

[1]祝云华,刘新荣,梁宁慧,等.裂隙岩体渗流模型研究现状与展望[J].工程地质学报,2008,16(2):178-183.(ZHU Yun-hua,LIUXin-rong,LIANG Ning-hui,et al.Current research and prospects in modeling seepage field in fractured rock mass[J].Journal of Engineering Geology,2008,16(2):178-183.(in Chinese))

[2]周志芳.裂隙介质水动力学原理[M].北京:高等教育出版社,2007.

[3]王媛,速宝玉.裂隙岩体渗流模型综述[J].水科学进展,1996,7(3):276-282.(WANG Yuan,SU Bao-yu.Comment on themodels of seepage flow in fractured rock masses[J].Advances in Water Science,1996,7(3):276-282.(in Chinese))

[4]杨璐玲.岩体渗流场数值分析方法研究[D].天津:天津大学,2003

[5]汝乃华.梅山连拱坝右坝座的错动及其原因分析[J].水利学报,1988(9):28-35.(RU Nai-hua.The slip of the right abutment of Meishan multiple-arch dam and its analysis[J].Journal of Hydraulic Engineering,1988(9):28-35.(in Chinese))

[6]王媛,速宝玉.单裂隙面渗流特性及等效水力隙宽[J].水科学进展,2002,13(1):61-67.(WANG Yuan,SU Bao-yu.Research on the behavior of fluid flow in a singlefracture and its equivalent hydraulic aperture[J].Advances in Water Science,2002,13(1):61-67.(in Chinese))

[7]耿克勤,陈凤翔,刘光廷,等.岩体裂隙渗流水力特性的实验研究[J].清华大学学报:自然科学版,1996,36(1):102-106.(GENGKe-qin,CHEN Feng-xiang,LIUGuang-ting,et al.Experimental research of hydraulic properties of seepage flow in fracture[J].Journal of Tsinghua University:Science and Technology,1996,36(1):102-106.(in Chinese))

[8]魏进兵,邓建辉,高春玉,等.三峡库区泄滩滑坡非饱和渗流分析及渗透系数反演[J].岩土力学,2008,29(8):2262-2266.(WEI Jin-bing,DENG Jian-hui,GAOChun-yu,et al.Unsaturated seepage analysis and back analysisof permeability coefficientfor Xietan landslidein Three Gorges Reservoir area[J].Rock and Soil Mechanics,2008,29(8):2262-2266.(in Chinese))

[9]王环玲,徐卫亚,童富国.泄洪雾雨区裂隙岩质边坡饱和-非饱和渗流场与应力场耦合分析[J].岩土力学,2008,29(9):2397-2403.(WANG Huan-ling,XU Wei-ya,TONG Fu-guo.Coupled analysis of fracture rock mass slope saturated-unsaturated seepage field and stress field in flood discharge atomized rain area[J].Rock and Soil Mechanics,2008,29(9):2397-2403.(in Chinese))

[10]宋晓晨,徐卫亚.裂隙岩体渗流模拟的三维离散裂隙网格数值模型(I):裂隙网格的随机生成[J].岩石力学与工程学报,2004,23(12):2015-2020.(SONGXiao-chen,XU Wei-ya.Numerical model of three-dimensional discretefracturenetwork for seepage in fractured rocks(I):generation of fracture network[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(12):2015-2020.(in Chinese))

[11]卢刚,周志芳.降雨入渗下互层状裂隙岩体非饱和渗流分析[J].岩土工程学报,2008,30(9):1399-1403.(LU Gang,ZHOU Zhi-fang.Analysis of unsaturated seepage in inter-bed layered fractured rock mass with rainfall infiltration[J].Chinese Journal of Geotechnical Engineering,2008,30(9):1399-1403.(in Chinese))

[12]黄勇,陈静.岩体裂隙介质各向异性耦合模型研究[J].河海大学学报:自然科学版,2009,37(2):171-174.(HUANG Yong,CHENJing.Anisotropic coupled model for fractured rock medium[J].Journal of Hohai University:Natural Sciences,2009,37(2):171-174.(in Chinese))

[13]刘凤茹.复合土工膜选型及缺陷渗漏量试验研究[D].南京:河海大学,2005.