优先级保护的分布式动态频谱分配算法
李宴滨,汪李峰,魏胜群,魏政霞
(1.解放军理工大学通信工程学院,南京210007;2.中国电子设备系统工程公司研究所,北京100141;3.总参通信训练基地有线研究室,河北张家口075100)
1 引 言
近年来,随着无线用户数量及通信需求的急剧增加,可用频谱稀缺的现象越来越明显。研究表明,不是频谱资源不够用,而是频谱资源没有得到合理的应用:一方面非授权频段比较少并且用户多,比较拥挤;另一方面很多授权频段利用率很低,从联邦通信委员会的调查数据来看,已分配的频谱利用率在15%~85%[1]。认知无线电(CR)[2]作为一种新兴的技术,得到了越来越多的关注。CR可以通过学习,不断感知环境变化,并根据环境的变化对自身传输参数进行调整,从而保证可靠通信。认知无线电的一个重要应用是机会频谱接入,即在不对主用户造成干扰的前提下使用授权频谱,从而满足自身通信需求,因此可以对空闲的频谱进行有效利用。
无线通信中的认知用户本质上是一个自治的智能主体,他们之间对频谱的选择利用是一个相互影响相互交互的过程。博弈论主要用于研究具有对抗局势的模型,能够为相应的博弈过程找到纳什均衡点。因此,博弈论为动态频谱分配问题提供了一种新的方法和模型。
基于博弈论的动态频谱分配算法已经有了很多的研究。文献[3]针对不同的信道有不同的信道特征,而不同的用户有不同的需求,以达到最优的频谱利用率为目标设计了分配方法。文献[4-6]研究了分布式Ad Hoc网络中采用位势博弈,以最大化信干比为目标设计效用函数,而后两者分别就保护授权链路和OFDM机制进行了进一步的研究。文献[7]通过CSMA的方式接入信道,根据反馈信息估计成功接入的概率,在设计效用函数的时候,加入惩罚函数,通过学习方法达到相关均衡。文献[8]中作者应用匹配博弈提出了一种频谱分配算法,以最大系统总传输速率为目标,通过双向选择机制达到均衡点且为最优。文献[9]指出不同用户有不同的传输要求和传输类型,分别要求不同的传输速率,通过动态博弈达到均衡,有较好的频谱利用率和用户满足率。
上述文献大多只是单纯的分配信道,没有考虑发射功率的影响,而在能量受限的情况下功耗是很重要的参数。文献[10]提出了单信道ADP(Asynchronous Distributed Pricing)算法,可以实现功率和信道的联合分配,但是需要所有认知用户具有相同的通信需求。然而在实际情况中,往往会有相对来说更重要的用户,即高优先级用户。本文提出一种带有干扰价格因子的ADP算法,可以提高高优先级用户的性能。
2 系统模型
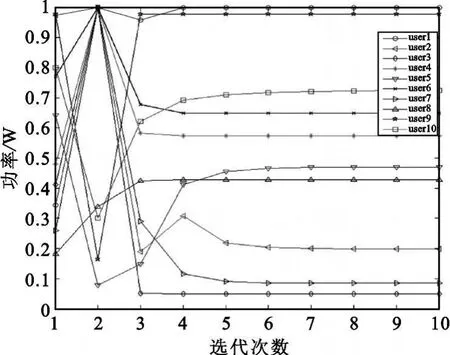
分布式CR网络如图1所示,可用信道集合为C={1,2,3,…,M},其中存在K条链路代表K个用户κ={1,2,3,…,K},M 图1 网络拓扑图Fig.1 The network topology 其中,k用户选择的信道用φ(k)表示,φ(k)∈ Μ,k用户在信道φ(k)上选择的功率用表示∈[0,pmax],传输质量可以表现在误码率上,同样可以表现在信干噪比上。k用户在信道φ(k)上的信干噪比为 式中,hkk表示k用户发送端和接收端之间的增益,hjk表示j用户的发送端到k用户的接收端之间的增益。 博弈论[11]是研究具有对抗或竞争现象的数学理论和方法,它是现代数学的一个分支,也是运筹学的一个重要学科。作为一种研究决策过程的数学工具,博弈论可以有效地预测决策结果,并选择最佳策略[12]。 在频谱分配模型中,各个认知用户选择的信道和功率不仅影响自己的性能,同时也影响其它邻居用户的性能。认知用户本质上是一个自治的智能主体,他们之间对频谱资源的选择利用是一个相互影响相互交互的过程,因此,博弈论为动态频谱资源分配问题提供了一种新的方法和模型[13]。 一般的博弈模型可以用下式表示: 式中,N={1,2,3,…,n}表示博弈的参与者,在频谱分配模型中就是参与分配的用户;Si为第i个用户的策略空间,即认知用户的传输参数,在本文中表示认知用户所选择的信道和功率;Ui表示第i个用户的效用函数,它是所有用户的策略空间映射到实数的一个函数,由于每个用户的收益不仅与自己选择的策略有关还与其它用户选择的策略有关,参与者的效用函数Ui是自身策略 si和其竞争对手策略 s-i的函数,根据博弈者的喜好不同有不同的效用函数。 博弈分析中一个重要的概念就是纳什均衡,所谓纳什均衡是指所有参与者选定的策略的组合,当且仅当: 这组策略就是纳什均衡。公式(3)表示的意思是任何一个参与者单独改变行动,都会使其自身的效用函数降低。 本文应用了动态博弈(Dynamic Game)[11]模型。动态博弈是指参与人的行动有先后顺序,而且后行动者可以观察到先行动者的选择,并据此做出选择,先行动者的选择影响后行动者的选择空间。本文运用简单的迭代来指配各用户的博弈次序,重复进行动态博弈过程直至收敛。一个动态博弈过程为一个迭代周期,一个迭代周期分为K个时隙(K= N ),每个时隙对应一个用户,即每个时隙中有一个用户进行决策,所有用户依次进行决策。 对于每个用户,无论其优先级的高低,由于各个信道的带宽相同,其信干噪比直接影响到其效用,我们可以定义k用户的效用为 对于所有用户θk为相同参数,所以用户的效用函数只跟SINRk有关系。我们的设计目标是各用户选择信道和功率值使得: 若各个用户的效用函数定义为式(4),则每个用户一定选择最好的信道,并且以最大功率发送,另外也不能有效保证高优先级用户的特殊需求,这种自私的发送方式往往会降低整个系统的性能,使博弈过程的纳什均衡偏离全局最优策略,即个人理性与集体理性冲突。因此,分布式节点间既要保证自身的正常工作和通信需求,又要考虑对其它节点的干扰,应用合作博弈设计算法可以有效解决上述问题。 原来的ADP算法中[10]定义干扰价格如下: 干扰价格表示了用户所受干扰每增加一个单位带来的收益的降低,每个用户轮流发布干扰价格,在知道其它用户的干扰价格时,定义用户的效用函数如下: 式中,第一项为其自身收益,第二项为代价函数。由于网络中用户有不同的优先级,原来的算法不能体现优先级的区别,因此,从干扰价格的发布上进行改进,加入干扰价格因子α。改进后的干扰价格定义为 式中,αk为用户j的干扰价格因子。 文献[10]中我们可以认为对于所有用户 αk=1,从式(6)和式(7)可知,此时对于用户 k,自身收益和代价函数的权值是一样的,因此,可以达到网络的整体收益最大。然而,为了提高高优先级用户的性能,就必须牺牲网络中其它用户或其中一部分用户的性能。高优先级用户在发布干扰价格的时候可以使αk的值大于1,这样其它用户在选择与其相同的信道时第二项的代价函数值增大,使其效用函数减小,从而选择其它效用函数值高的信道或者减小发射功率,达到了对高优先级用户的保护。如果干扰价格因子取小于1的正实数时,则表明此用户更重视对其它用户的干扰,优先级为最低的用户类型。 每个认知用户都维持一个干扰价格矩阵、各用户的信道使用矩阵和一个增益矩阵,每个用户异步执行分配算法,具体的算法流程如下: (1)各个用户参数的初始化,包括信道选择、功率值、干扰价格; (2)若当前时隙属于用户k,则用户k执行以下步骤: 1)根据公式(7),计算使用各个信道时效用函数的最大值及其效用函数最大时的功率值pk; 2)选择其中效用函数最大的信道及其对应的功率值; 3)根据公式(8)计算其干扰价格,向外发布干扰价格和所选择的信道; (3)各用户更新干扰价格和信道使用矩阵; (4)所有用户轮流进行流程2,直至收敛。 本文使用Matlab建立认知无线电系统的仿真平台,背景噪声 n0=10-2,每个用户的传输功率的范围pmax=1,仿真场景中可用信道数为4,存在10个认知用户,其中2个为高优先级用户,10个发送节点随机分布在3×3的区域内,其相应的接收节点随机分布在距离发送节点距离大约为1的范围内,链路增益定义为距离的函数,假设各个信道增益相同,即,β为固定的参数。 设置仿真迭代次数为20,仿真结果如图2~5所示。初始信道分配状况和收敛后的信道分配状况见表1。 表1 算法前后信道分配状况对比Table 1 The comparison before and after the channel allocation 图2~5分别显示了迭代过程中所有用户的发射功率、信道选择、干扰价格以及信干噪比的变化情况,并且分别在 9、3、8、9 次达到收敛状态 ,因此 ,改进后的算法具有极快的收敛速度,能够很快达到纳什均衡,可以很好地适应环境的变化。同时,从图2中可以看出,并不是所有的用户都以最大功率发送,达到了同时分配信道和功率的目的。 图2 功率更新Fig.2 Power update 图3 信道更新Fig.3 Channel update 图4 干扰价格更新Fig.4 Interference price update 图5 信干噪比更新Fig.5 SINR update 由于初始信道选择、初始功率、初始价格、产生的拓扑都是随机的,故达到的纳什均衡有可能是不一样的,为比较使用改进后ADP算法和原来ADP算法高优先级用户的信干噪比的前后差别,需要运用统计的方法得到平均信干比。选取一个随机产生的拓扑和随机产生的初始信道分配,分别使用原来算法和改进后的ADP算法进行上述仿真过程1 000次,分别记录其结果,最后取平均,如图6所示。此柱状图有两组数据,前面一组是改进前的信干噪比,后一组为改进后的信干噪比,高优先级用户为用户9、10,干扰价格因子为5,其它用户干扰价格因子为1。运用改进后算法提高了高优先级用户的性能,但是由于价格因子的作用使得低优先级用户减少对高优先级用户的干扰,低优先级用户有不同程度的性能损失。因此高优先级用户性能的提高是以低优先级用户的性能损失为代价的。 为了得到干扰价格因子对用户性能的影响,下面以用户10为例,仿真过程与以上类似,得到干扰价格因子分别为 0、0.1、0.5、1、5、10、30、50 时的性能变化情况,如图7所示。可以看出,用户10随着干扰价格因子的不断增大信干噪比不断增大,这与理论是相符的。随着干扰价格因子的增大,其性能增长速度减慢直到不再变化,这是因为干扰价格因子大到一定程度,影响用户性能的因素主要是自身的链路增益等其它因素,而不是其它用户的干扰。 图6 两种算法性能Fig.6 Performance of the two algorithms 图7 不同干扰价格的性能Fig.7 The performance of different interference price 本文利用重复博弈和动态博弈对认知无线网络中的分布式动态频率选择和功率控制策略进行了研究,在ADP算法的基础上引入干扰价格因子,从而达到提高高优先级用户性能的目的。通过认知用户之间进行合作博弈来共享频谱资源,减小干扰,提高算法性能。仿真结果表明,改进后的算法可以实现信道和功率的联合分配,可以达到纳什均衡并且具有极快的收敛速度,在存在不同优先级用户的情况下可以一定程度提高高优先级用户的性能,但是是以牺牲其它用户性能为代价。另外,实际系统中用户可能存在欺骗行为,本文未曾涉及,这是今后的研究重点。 [1]Federal Communications Commission.Spectrum policy task force[R]//Report of Spectrum Efficiency Working Group.Washington:FCC,2002. [2]Mitola J III.Cognitive Radio:An Integrated Agent Architecture for Software Defined Radio[D].Sweden:Royal Institute of Technology,2000. [3]Liu Jishun,Shen Lianfeng,Song Tiecheng,et al.Demand-Matching Spectrum Sharing Game for Noncooperative Cognitive Radio Network[C]//Proceedings of 2009 International Conference on Wireless Communications&Signal Processing.Nanjing:IEEE,2009:1-5. [4]Nie N,Comaniciu C.Adaptive channel allocation spectrum etiquette for cognitive radio networks[J].Mobile Networks and Applications,2006(11):779-797. [5]冯春燕,郭义武,薛钰,等.授权链路保护的频谱分配算法[J].电子科技大学学报,2008,37(6):855-859.FENG Chun-yan,GUO Yi-wu,XUE Yu,et al.Spectrum Allocation Algorithm Based on Protecting Licensed Link[J].Journal of University of Electronic Science and Technology of China,2008,37(6):855-859.(in Chinese) [6]Quang Duy La,Yong Huat Chew,Boon-Hee Soong.An Interference Minimization Game Theoretic Subcarrier Allocation Algorithm for OFDMA-based Distributed Systems[C]//Proceedings of the 28th IEEEConference onGlobal T elecommunications.Honolulu,Hawaii,USA:IEEE,2009:2799-2804. [7]Michael Maskery,Vikram Krishnamurthy,ZHAO Qing.Decentralized Dynamic Spectrum Access for Cognitive Radios:Cooperative Design of a Non-Cooperative Game[J].IEEE Transactions on Communications,2009,57(2):459-469. [8]Chengquan An,Liang Zhang,Wenyan Liu.A Spectrum Allo-cation Algorithm Based On Matching Game[C]//Proceedings of the 5th International Conference on Wireless Communications,Networking and Mobile Computing.Beijing:IEEE,2009:1626-1628. [9]Tao Jin,Chunxiao Chigan,Zhi Tian.Game-theoretic Distributed Spectrum Sharing for Wireless Cognitive Networks with HeterogeneousQoS[C]//Proceedings ofGlobal Telecommunications Conference.San Francisco,CA,USA:IEEE,2006:1-6. [10]Huang J,Berry R,Honig M L.Spectrum Sharing with Distributed Interference Compensation[C]//Proceedings of IEEE DySPAN Conference.Baltimore,USA:IEEE,2005:88-93. [11]范如国,韩民春.博弈论[M].武汉:武汉大学出版社,2006.FAN Ru-guo,HAN Min-chun.Game Theory[M].Wuhan:Wuhan University Press,2006. [12]Varian H R.Microeconomic Analysis[M].New York,USA:W.W.Norton&Company,1992. [13]Allen BMackenzie,Luiz A Dasilva.Game Theory for Wireless Engineers[M].San Rafael,CA:Morgan and Claypool,2006.

3 博弈模型
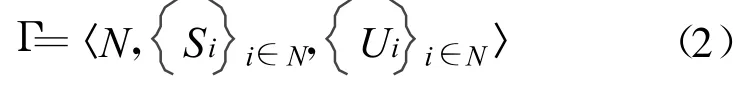

4 算法设计的目标和效用函数
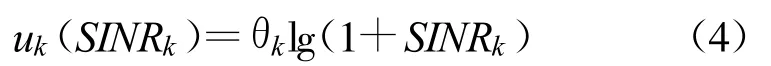




5 算法流程
6 仿真结果






7 结 论

