旋挖钻机伸缩钻杆稳定性分析

卜长根 张兴辉

(中国地质大学(北京)工程技术学院 北京 100083)

在高层建筑、道路桥梁、大坝等基础施工中,旋挖钻机的应用越来越广泛。伸缩钻杆是旋挖钻机的一个关键部件,在旋挖钻机深孔施工中,随着钻孔的不断加深,钻杆伸出得越来越长,而从上到下伸缩钻杆变得愈来愈细,技术人员如何设计阶梯变截面伸缩钻杆,确保钻孔施工过程中,孔深和地层变化不至于加压失稳而造成伸缩钻杆破坏。因此,有必要对伸缩钻杆进行稳定性分析。

伸缩钻杆相当于一种变截面杆件,变截面压杆稳定临界力的计算是工程设计中经常遇到的问题,但从目前来看,对于变截面构件稳定性的计算,还没有一种统一的设计方法。严格地讲,压杆稳定临界力的计算是非线性问题,而且对于不同的截面,杆件变形微分方程的形式不同,求解十分复杂,只有几种特殊情况(如等截面)才能用欧拉方程求解。国内多数情况基于有限元法,研究变截面定长度杆的稳定性,国外近年主要基于非线性理论和数值法研究定长连续一致变截面杆(悬臂梁)稳定性问题。对于旋挖钻机伸缩钻杆,随钻孔延深,内层钻杆伸出、顶部钻杆依次变空、截面依次变化,边界变化等对钻杆稳定性的影响稍缺乏系统研究。

1 结构稳定性分析理论基础

1.1 伸缩钻杆数学模型

弹性体总势能就是弹性体的形变势能U和载荷系统的外力势能W之和。当结构系统是保守系统,外力变形过程中保持其大小和方向不变,外力功只和弹性体变形体前后两个状态有关,而与变形过程无关。这样可以把外力做功看成一个保守的有势力场势能,外力势能等于结构上的每一个外力所作的功W。

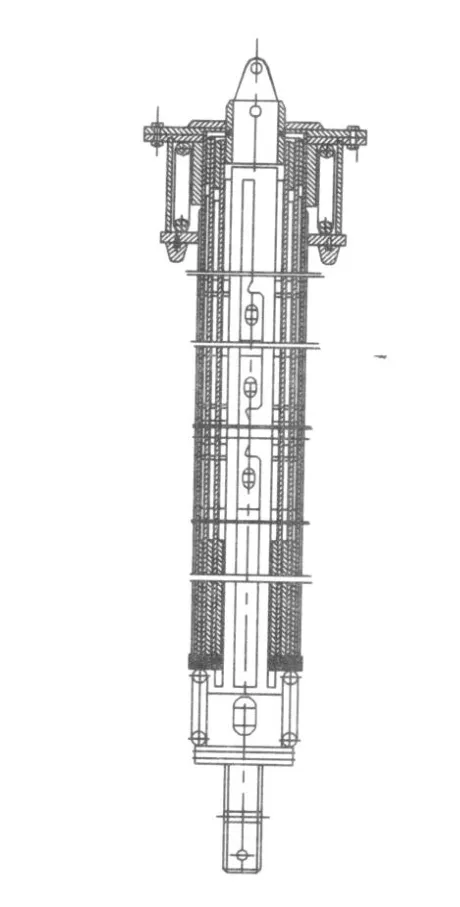
图1 CM V-1500钻机伸缩钻杆

外力势能:

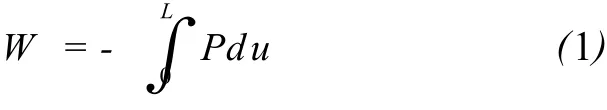
其中:u是在x方向上的位移。

应变能为:

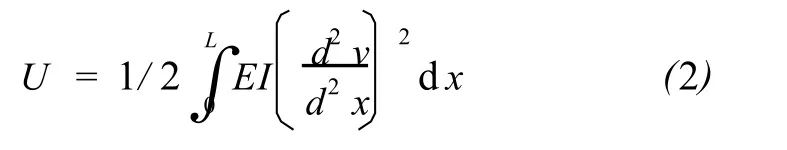
系统总势能为:

式(3)中d u通过图2几何关系d s、d v、d x变换得:

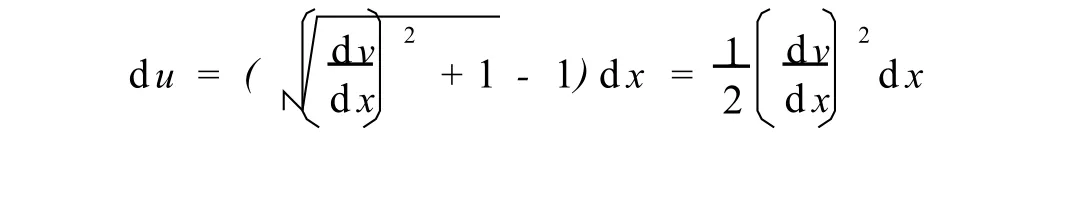
图2 受压伸缩钻杆力学模型

总势能公式转化为:

引进形函数 N,令 v=[N]{δ},由最小势能原理可知,在所有几何可能位移中,真实位移使得总势能取最小值,即,可得到最小势能,由总势能对求偏导得:

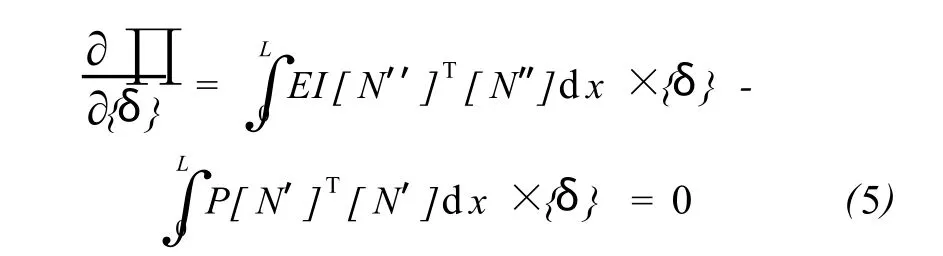
将(5)式简化成为:

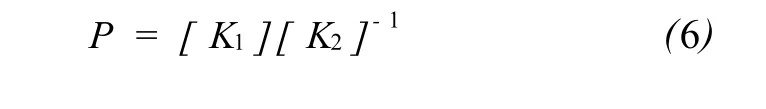
其中:

经过实地走访发现，农村的商业银行在小额信贷的发放方面，并未达到预期的目标，主要由于年利率高出了农户的预期值。同时，受产业投资回报率的限制,农业产业的平均回报率不高，农业生产收益也有很大不确定性，银行对农户及农业制定的贷款利率普遍偏高，这种高利率提高了农户的生产融资成本，加剧了农户融资难的现状[3]，影响了农民的贷款积极性，不利于乡村振兴战略的实施。

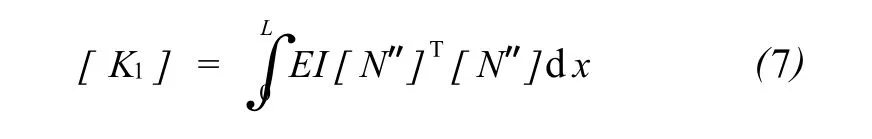
根据公式(7)、(8)计算出各段钻杆的弹性刚度矩阵[K1]i(i=1,2,3,4,5),几何刚度矩阵[K2]i(i=1,2,3,4,5),然后叠加成整体刚度矩阵和。

1.2 加入边界条件

钻杆在逐渐伸出过程中,最下面一段可以看成为实心圆柱,上面各段为中空圆柱,依次伸出一节,二节……五节,顶部钻杆依次变空,把每一截当成一个梁单元。当短螺旋钻头刚刚接触孔底土体时,这时只是限制钻杆的平移自由度,对钻杆的旋转自由度限制程度比较小,因此钻杆底部可以作为铰支约束,如图3所示。当钻头全部钻入地层后,钻头的平移自由度和旋转自由度都受到约束,这时钻杆底部可视作固定端,如图4所示。下面就从这两种情况入手,来施加边界条件。

图3 钻进开始

图4 钻进结束

(1)两端铰支

两端节点的位移δ1=0和δ6=0,而偏转角不为0,与之相对应的刚度矩阵要作修改,将刚度矩阵、[K1]1+2+3+4+5、[K2]1+2+3+4+5的第一行 ,第一列 ,第十一行,第十一列划去。

(2)上端铰支 下端固定

下端节点6的位移δ6=0,转角θ6=0,将刚度矩阵[K1]1+2+3+4+5、[K2]1+2+3+4+5的第十一行、第十一列,第十二行、第十二列划去;上端节点1的位移δ1=0,偏转角θ1不为0;将刚度矩阵[K1]1+2+3+4+5、K21+2+3+4+5的第一行、第一列划去。

1.3 求临界载荷

将[K1]1+2+3+4+5,[K2]1+2+3+4+5,带入公式(6),求得:

从上式可得到一个由矩阵表达的解,再由|P-λI|=0解出其特征值λ,即为临界载荷 Pcr=λ。

2 伸缩钻杆稳定性有限元计算

2.1 伸缩钻杆基本参数与建模

旋挖钻机CMV-1500伸缩钻杆由五节钻杆组成,选用BEAM 3单元,将钻杆简化为圆环截面。各段钻杆材料45M n钢,弹性模量为2.1E11Pa,泊松比0.3,各段钻杆的长度为13m,截面粗细不同,其截面惯性矩不同,表1是CMV-1500钻杆全部伸出后各段基本参数。

建立实体模型,根据坐标生成关键点,连接关键点生成线,并进行单元划分,注意划分时将各段钻杆与其对应的截面属性和实常数属性一一对应,然后对模型加载荷和边界条件。

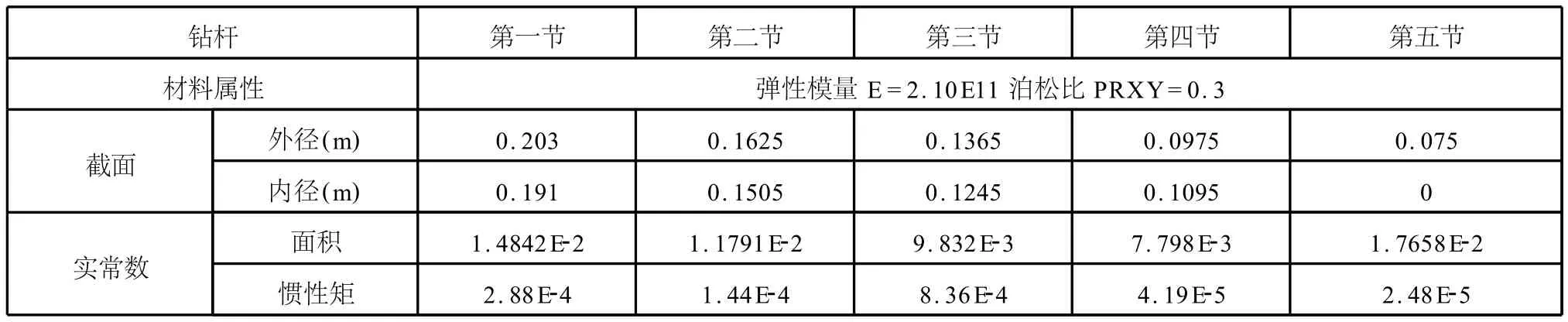
表1 CM V-1500伸缩钻杆基本参数表

2.2 求解

屈曲求解过程分为两个过程,首先进行静力求解,选择静力分析,打开预应力开关,进行静力求解;静力求解完成后,重新进入求解器,进行屈曲求解,选择屈曲分析类型,设置分析选项(将特征值提取数设为1),进行屈曲求解。

2.3 结果分析

(1)两端铰支五节钻杆全部伸出后的屈曲变形见图5。从图中可以看出此时的临界载荷为 Pcr=FREQ=30.35kN,最大位移为2.0189cm。

图5 两端铰支屈曲变形图

(2)上端铰支、下端固支五节钻杆全部伸出后的屈曲变形见图6,此时的临界载荷为 Pcr=FREQ=68.203kN,最大位移为1.3917cm。

根据不同孔深、不同边界时,伸缩钻杆顶端临界载荷的计算数值,画出临界载荷和孔深的关系曲线见图7。

从图7可以看出,在底端固定,顶端铰支情况下,伸缩钻杆的临界力载荷大约等于两端铰支情况下的两倍。从钻杆设计角度来看,以两端铰支方式设计,偏于安全。

不同约束形式,孔深对临界力影响较大。当钻杆伸出较短时,不同约束对钻杆临界力的影响很大,随着钻杆的逐渐伸长,约束情况对临界力的影响变小。无论在哪种约束情况下,钻深在达到一定深度(约30m),临界力随深度的加深递减的很快,随后随深度的加深递减变缓。

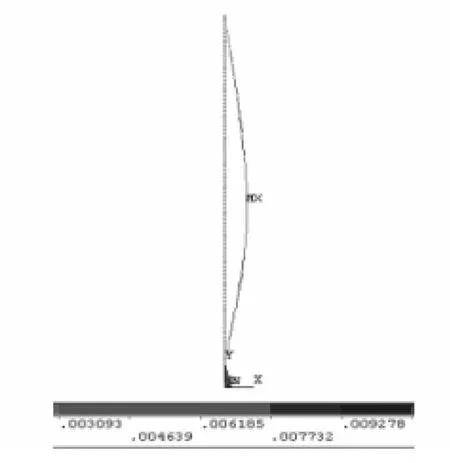
图6 上端固定、下端铰支屈曲变形图

图7 孔深-临界力曲线

大部分钻机给进压力大约都在150kN左右,从计算数据来看,在钻孔深度超过一定深度后,失稳临界载荷很小,应避免加压钻进引起钻柱失稳,防止孔底钻头(钻斗)与较细钻杆联结处产生较大应变而断裂。

3 结语

(1)当钻孔较浅时,约束边界对钻杆临界力的影响很大,随着钻孔的加深,约束边界对临界力的影响变小;在某一深度范围内,临界力随孔深的变化递减很快,随后将明显变缓。

(2)在钻孔到一定深度后,失稳临界载荷很小,应避免加压钻进引起钻柱失稳,引起较细钻杆断裂;从钻杆设计角度来看,以两端铰支方式,设计使用伸缩钻杆偏于安全。

1 王守仁、屈建中、李吉.变截面压杆稳定性临界力计算的有限元素法.沈阳航空工业学院学报,1995(4)

2 戴保东、郑荣、吉子轩.变截面压杆稳定性计算的有限元法.山西机械,2000(3)

3 张煜.变截面压杆稳定性分析的矩阵传递法.贵州工业大学学报,2000(5)

4 卞敬玲、王小岗.变截面压杆稳定计算的有限单元法.武汉大学学报,2002(4)