高师专科学生数学文化背景的调查与研究

张 伟，蔡银英

（重庆教育学院 经济贸易系，重庆400067）

高师专科学生数学文化背景的调查与研究

张 伟，蔡银英

（重庆教育学院 经济贸易系，重庆400067）

采用问卷调查的方式，了解高师专科数学教育专业学生的数学文化背景状况，分析了学生在数学文化背景方面的强势与弱势，提出了相应的数学课程改革建议。

数学文化；教育调查；数学课程

1 数学文化的界定

数学文化是指一个人通过某种特定的学习途径获得一定的数学知识之后，所表现出来的特有的行为准则、思想观念及对待事物的态度。数学文化是由数学的思想、知识、方法、技能、理论等所辐射出来的能与相关文化领域结合为一体的一个具有强大精神与物资功能的动态系统。［1］

数学文化包括以下几个方面。（1）知识成分：包括数学理论知识、数学问题、数学语言等。（2）能力因素：包括数学应用能力、将问题通过适当途径而数学化的能力、逻辑论证能力、计算能力、问题解决能力、数学表达能力。（3）数学观念：包括数学思维方式、思想观点、情感态度、价值观念。［2］

虽然数学文化的内容涵盖了一个人数学修养的各个方面，但是它更强调当一个人的数学知识与其它各个领域的知识能力相融合之后所表现出来的综合素质。

2 调查目的

本项调查研究的目的是希望通过一种直接的可操作方式，比较全面地调查与分析高师专科学生这一“准教师”群体的数学文化背景现状、水平以及强势与弱势，明确高师专科数学教育专业课程改革的方向，这有利于将基础教育改革与高师数学课程改革有机地结合起来。

2001年教育部制定与颁布的国家《数学课程标准》指出：“数学是人们生活、劳动与学习必不可少的工具，能够帮助人们处理数据、进行计算、推理和证明，数学模型可以有效地描述自然现象和社会现象；数学为其他科学提供了语言、思想和方法，是一切重大技术发展的基础；数学在提高人的推理能力、抽象能力、想象力和创造力等方面有着独特的作用；数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分。”［3］

从一定的角度讲，数学科学对于人类文明的推动作用更主要地是通过数学的文化层面而实现的。深入地了解与研究高师专科学生的数学文化状况是一件极有价值的工作，有利于加强数学教育专业的课程建设。

3 问卷设计

问卷从以下几个方面调查了解高师学生的数学文化背景知识：

（1） 数学知识。即包括数学理论知识。也包括数学史知识。

（2） 数学能力。包括形式推理与形式计算能力，同时也包括猜测估算等非形式数学能力。

（3） 与数学相关的情感态度、体验与经历。

（4） 数学观念。包括数学地思考与判断问题的方式以及由数学知识而形成的价值观。

4 调查对象及方式

问卷调查对象：重庆教育学院数学系2001级专科学生67人。

问卷调查采用现场发放问卷，当场解答，解答后当场回收答卷的方式。答卷时间为100分钟。

本次问卷调查共发出问卷67份，收回64份，回收率 95.52%

5 调查结果

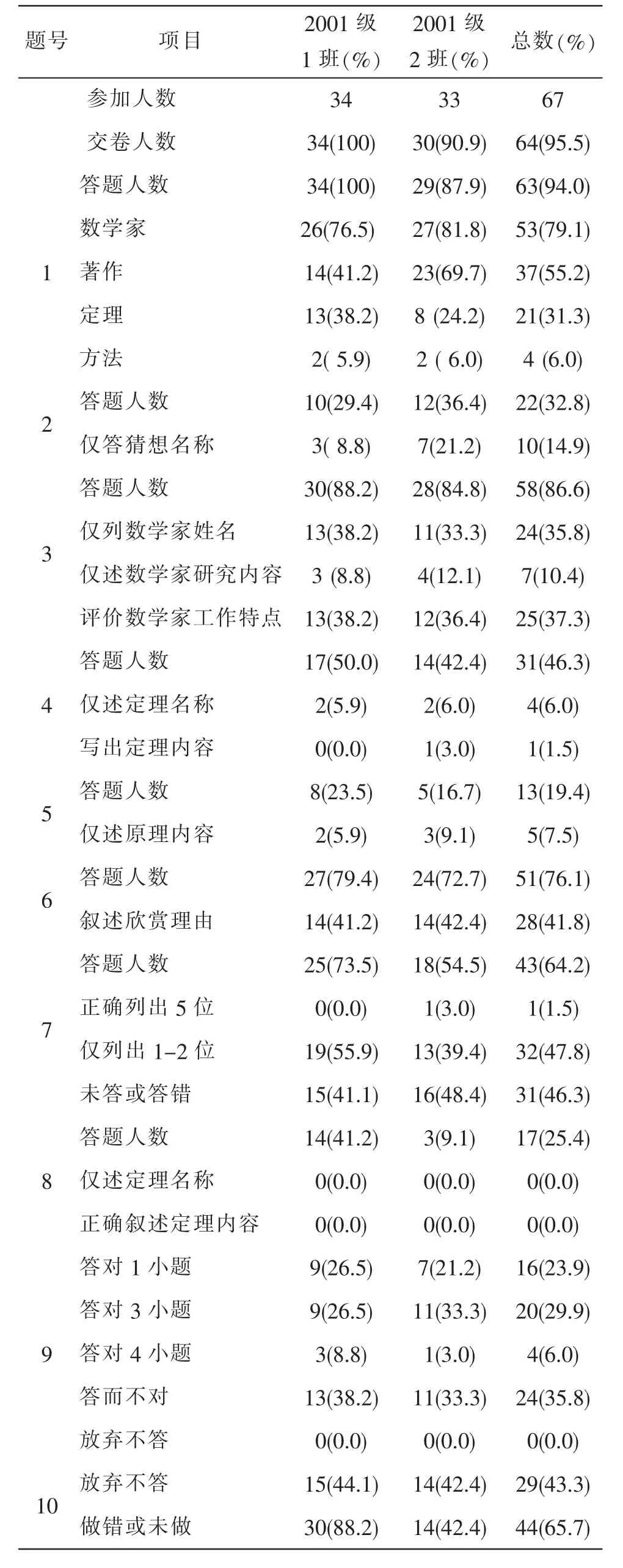
表1 答题情况统计表

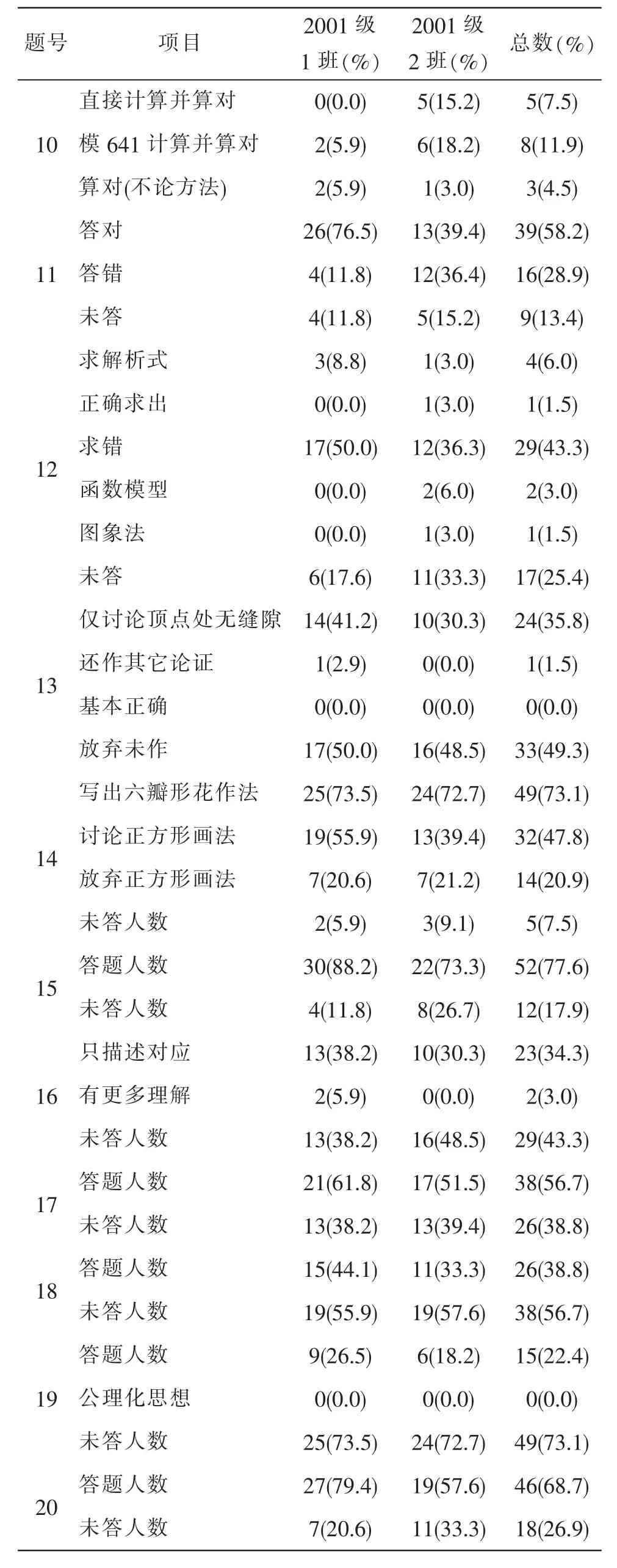
题号 项目 2001级1班（%）2001级2班（%） 总数（%）10直接计算并算对 0(0.0) 5(15.2) 5(7.5)模 641 计算并算对 2(5.9) 6(18.2) 8(11.9)算对(不论方法) 2(5.9) 1(3.0) 3(4.5)11答对 26(76.5) 13(39.4) 39(58.2)答错 4(11.8) 12(36.4) 16(28.9)未答 4(11.8) 5(15.2) 9(13.4)12求解析式 3(8.8) 1(3.0) 4(6.0)正确求出 0(0.0) 1(3.0) 1(1.5)求错 17(50.0) 12(36.3) 29(43.3)函数模型 0(0.0) 2(6.0) 2(3.0)图象法 0(0.0) 1(3.0) 1(1.5)未答 6(17.6) 11(33.3) 17(25.4)13仅讨论顶点处无缝隙 14(41.2) 10(30.3) 24(35.8)还作其它论证 1(2.9) 0(0.0) 1(1.5)基本正确 0(0.0) 0(0.0) 0(0.0)放弃未作 17(50.0) 16(48.5) 33(49.3)写出六瓣形花作法 25(73.5) 24(72.7) 49(73.1)讨论正方形画法 19(55.9) 13(39.4) 32(47.8)放弃正方形画法 7(20.6) 7(21.2) 14(20.9)未答人数 2(5.9) 3(9.1) 5(7.5)15 答题人数 30(88.2) 22(73.3) 52(77.6)未答人数 4(11.8) 8(26.7) 12(17.9)14只描述对应 13(38.2) 10(30.3) 23(34.3)有更多理解 2(5.9) 0(0.0) 2(3.0)未答人数 13(38.2) 16(48.5) 29(43.3)17 答题人数 21(61.8) 17(51.5) 38(56.7)未答人数 13(38.2) 13(39.4) 26(38.8)18 答题人数 15(44.1) 11(33.3) 26(38.8)未答人数 19(55.9) 19(57.6) 38(56.7)16 19答题人数 9(26.5) 6(18.2) 15(22.4)公理化思想 0(0.0) 0(0.0) 0(0.0)未答人数 25(73.5) 24(72.7) 49(73.1)20 答题人数 27(79.4) 19(57.6) 46(68.7)未答人数 7(20.6) 11(33.3) 18(26.9)

6 分析与评述

6.1 分类分析

我们首先把问卷中的20个问题作简单分类，比较各类问题的答题人数并加以分析。

第一类：题1-8。主要检测学生对于数学发展史的一般性了解，其中包括中外数学家、数学研究成果、数学问题与猜想等。平均每题答题人数37人，占交卷总人数的58.2%。

第二类：题9-14。主要检测学生的数学知识覆盖面与知识的灵活应用能力。平均每题答题人数49人，占交卷总人数 76.6%。

第三类：题15-20。主要检测学生对数学知识的反思精神。平均每题答题人数35人，占交卷总人数的55.2%。

第二类问题的答题人数最多，这说明学生的学习积极性很高，答题的态度很认真，能对新问题有所的思考。从第一类问题的答题情况可以看出：学生具备一定的数学史知识，对数学发展状况有一般性的了解。由于我系2001级没有开设数学史课程，因此学生的数学史知识基本是由学生自学获得的，这说明学生对数学史知识有一定的兴趣，自主阅读过相关参考书籍。三类问题相比，学生对数学知识的反思性最差。

6.2 重点题目分析

题1 简述你对中国古代数学的认识（数学家、著作、定理、方法）

分析 这是20个问题中答题人数最多的一个题。但是大多数（79%）人只能说出数学家的名字，而仅有6%的人对中国古代数学家的工作方法有一定的认识。可见大部分学生对于数学的发展状况仅有比较粗浅的了解，这点从题2与题3的答题结果也可以看出来。

题5 叙述祖暅原理，并谈谈通过什么途径可以发现这一原理。

评述 祖暅原理本来是出现在中学数学中的几何内容，但仅有7.5%的人能陈述这一原理，竟然没有人能正确的理解祖暅原理的发现途径。

题6 说一个你最欣赏的数学定理，并谈谈你为什么欣赏它。

评述 这是一道容易被传统教学思想忽视的问答题。在各种能力因素中对学科价值的微观鉴赏能力是一种十分重要而又容易被忽视的能力。从整体上看，学生对该题的回答并不令人满意。只有76.6%的学生回答了这一问题，而且仅41.8%的人回答了对定理的欣赏理由。

题8 写出一个1900年之后才被发现的数学定理。

评述 竟然没有学生能完整的说出一个20世纪的数学定理。学生对于20世纪现代数学知识的贫乏程度令人吃惊，我们的专业课程中应该尽快地增加通向现代数学的窗口。

③在c的盖玻片一侧滴加1滴pH4.4的酸雨模拟液，用吸水纸在对侧吸引。3 min后拍照记录。然后用红墨水染色，观察细胞核着色情况，3 min后再拍照记录。

题9 选择两个小题，并算出结果：

评述 这是一个传统的数学练习题，解题所用的知识也是传统的课程知识，从统计表中可以看出参加问卷调查的学生都对该题进行了解答。但是多的学生没有一道题的解答正确，这说明这一部分学生的专业知识极不扎实，需要我们在平时的教学工作中多加注意。

题10 数学家欧拉发现641整除232+1。试证明这一结论。

分析 这是《初等数论》教材中的一道练习题，解这道题即使对于一个初中学生甚至对于一个小学生来说都不困难，因为要计算出232+1，只需要计算4*1024*1024*1024+1＝4294967297，再用 641 作一次除法，整个过程都是不复杂的算术运算，没有任何特别的困难。但是，使人难以理解的是有高达43.3%的学生放弃了该题，仅有7.5%的人用上面的简单算术运算正确地解答出这个问题，另有11%的人采用模641的同余算法，其他22.4%的人都无法完成这道简单的算术问题。

评述 对于已有一定数学文化素养的大学数学专业学生来说，重要的不是怎样解这道题，而是这道题的背景含义。早在欧拉之前100年，伟大的法国数学家、猜想大师费马认为232+1是一个素数，100年中人们实际上无法知道232+1究竟是素数还是合数，直到欧拉才发现了费马的这一猜想是错误的。不能把欧拉的这一工作看成一个简单的算术问题。虽然验证641整除232+1并不困难，但知道641是232+1的因子却非常困难。欧拉的这一工作是一项真正的数学发现，这项发现从费马到欧拉经历了整整一百年漫长的时间。

题12 圆口尖底的圆锥形量杯，在圆锥的一条母线上标有刻度.当上口径与锥高一定时，杯内所装溶液体积V是刻度x的函数.请你用适当方法描述这个函数。

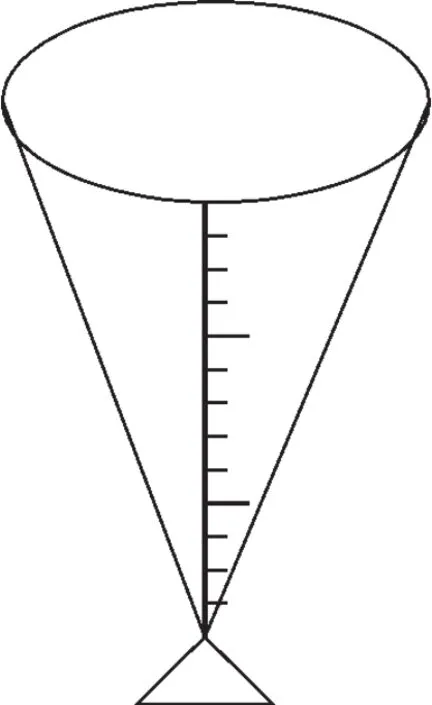
分析 本题并没有要求一定要具体地计算出函数V＝f（x）的精确解析表达式，但多数学生都选择计算解析式的做法。简单直接的描述这个函数的方法就是直观的说明V与x的立方成正比，即V＝ax3。

评述 在许多实际应用问题中，人们并不是一开始就关心函数的精确解析表达式，在大多数情况下中，人们首先关心函数模型的类别，根据函数模型的类别就能判断函数的一些主要性质.从本题的解答情况来看，学生解题的针对性不够，对解题目标的自主判断力不够。

评述 这是一道非传统的练习题，既有形式推理又有猜测发现，对于高师学生来说只有把数学知识融合为一种真正的数学文化背景知识，这样的知识才是具有启发价值的知识。但是目前我们的教学环节中这种融合和转化工作还做得不够，学生的自我融合和转化能力还很差。

题18 简述一次你最成功的数学发现或数学知识的应用。

题19 中央电视台《实话实说》节目“人体特异功能话题”中，一位专家谈到科学研究中的“奥卡姆剃刀”法则，这个法则要求在解释自然现象时尽可能不作“存在某个未知实体”的假设，谈谈你怎样从数学背景的层面上理解“奥卡姆剃刀”法则。

这是一个与“公理系统的数学推理”的推理范式有关的问题。解释“人体特异功能”的一个最简单办法就是承认某个未知物质的存在，这种未知的物质支持特异功能.但是这种方法毫无科学推理可言，科学推理是在仅仅只承认原有公理系统的条件之下进行“命题演绎”。当然命题演绎并不是数学推理的全部，数学推理也不排斥“不完全归纳法”，但是不完全归纳法只能发生在建立公理系统的过程当中。因此数学推理把“建立公理系统”与“命题演绎”这两件事分得清清楚楚，这就是数学的推理范式，它也正逐渐成为其他科学分支的推理范式。

7 结论和建议

通过问卷调查与分析，我们总结归纳出以下结论：

（1）高师数学教育专业的学生对数学史知识有一定的兴趣，但大多数学生都只是对中外著名的数学家的人名、研究工作以及古代重要的数学著作等有一般性的了解。

（2）学生的现代数学知识相当贫乏，竟然没有学生能完整的说出一个20世纪的数学定理。

（3）评价与鉴赏能力是一项重要的数学能力，传统的数学教育对于这项数学能力重视不够，目前学生的这项能力比较薄弱。

（4）学生对数学知识的反思做得不够。数学知识转化为学习者的数学文化背景要经历一个相当复杂的过程，一方面需要老师的指导，另一方面更需要学生不断的反思与融合。

（5）学生普遍缺乏探索和创造的经历。主动探索与创造必然会注意到前人数学发现的途径，但是几乎没有人知道祖暅原理产生的过程。

根据以上结论，我们建议在高师专科数学教育专业中增加数学史的课程，以提高对古今中外数学知识的了解；建议增加对现代数学相关内容有所介绍的课程，以提升其数学素养；建议加强数学思想和方法的教学，以提高其数学解题能力；建议加强数学文化知识的渗透，提高学生综合的数学修养，为今后从事的教学工作打下坚实的基础。

［1］张广祥.高师学生数学文化背景状况调查与分析［M］.西南师范大学学报（自然科学版），2004，（3）.

［2］傅赢芳 张维忠.对数学课程中有关数学文化的思考［J］.数学教育学报.2005，（3）.

［3］中华人民共和国教育部.全日制义务教育数学课程标准［M］.北京：北京师范大学出版社，2001.

［责任编辑 王南山］

Survey of and research on the mathematical cultural background of normal college three-year students

ZHANG Wei，CAI Yin-ying
（Department of Economy and Trade， Chongqing Education College， Chongqing 400067， China）

This paper， through the questionnaire survey， reveals the mathematical， cultural background of college three-year students majoring in mathematical education.It also analyses the students’ strengths and weaknesses in their mathematical， cultural background and forwards some suggestions for the reform of mathematical curriculum.

mathematical culture； questionnaire survey； curriculum reform

G658

A

1008-6390（2010）06-0034-04

2010-05-25

张伟（1966-），男，重庆万州人，重庆教育学院数学系副教授，硕士，研究方向：数学教育和教学；蔡银英（1976-），女，山西运城人，重庆教育学院数学系，讲师，研究方向：数学教育。