小波空域相关ICA跳频信号盲分离算法*
杜 纯1,周 薇2,高 健3,茹 乐1,孙 毅
(1.空军工程大学 工程学院,西安 710038;2.长沙大学 电子与通信工程系,长沙 410003;3.空军驻成都飞机工业公司军事代表室,成都 610092;4.空军驻上海胶带股份有限公司军事代表室,上海 200235)
1 引 言
跳频通信技术在军事通信系统中获得了广泛的应用。在电磁环境复杂的场合,如何有效分辨不同信源的信号,进而消除相互之间的干扰成为近期研究的热点问题。
由于跳频信号的低截获特性,使得对多跳频信号进行分离变得更为困难。目前,针对多跳频信号的分离方法可分为如下几种:采用多天线技术空间域分离方法;基于时域和频域分析及小波分析的时-频分离方法;利用多跳频信号统计特性和多天线技术而采用的独立分量分析(ICA)、盲分离方法[1]。很明显,多跳频信号在空-时-频域都有重叠的复杂环境下,上述方法中前两者具有局限性,后者则显示出很大的优势。
传统ICA方法[2-3]大多根据互信息极小基本原则对多导混合信号在时域进行处理来得到统计独立的分量(独立分量)。以Info-max法为例,算法要求多个混合分量输入,并且信源的概率密度分布特征决定了算法中累积分布函数的近似逼近的准确程度[4]。由于Info-max算法采用双曲正切函数作为累积分布函数的逼近,所以分离具有超高斯分布信源的效果要比信源是亚高斯分布型的效果好。这样,传统ICA方法对信源统计特性所提出的要求,同时也限制了其自身的应用范围。
另一方面,超分离问题也是多跳频信号分离需要面对的难题。传统ICA方法要求:天线馈源数目=目标信源数目+1,以小于目标信源数的天线馈源数求解ICA问题就是超分离问题。在多跳频信号盲分离领域,超分离问题具有重大的实际应用价值。
针对传统ICA方法的不足,本文将空域相关算法[5-6]引入了ICA过程,通过先在小波变换域进行分量盲分离来降低算法对不同概率分布信源的适应能力。小波空域相关函数包含着表征线性混合信号的混合特征信息,因此ICA算法可以通过空域相关函数求出解混矩阵而无需多导输入信号。同时,空域相关函数具有比小波系数更大的峰度,和文献[4]中提出的在小波域对混合信号进行盲分离的方法相比,基于小波空域相关的ICA方法具有更大的Kurtosis峭度,算法收敛速度更快。利用信号在不同尺度空间之间具有相关性的特点,空域相关一定程度上滤除了噪声,可以使ICA方法具有更好的抗噪性能。
本文首先给出ICA原理和信息极大化算法,然后提出了具体的空域相关ICA算法。仿真及对比结果表明了本文提出的空域相关ICA方法可较好地用于多跳频混合信号的分离与参数估计,在收敛速度、求解混矩阵、抗噪性能方面均具有优越性。
2 空域相关ICA算法的提出
空域相关ICA算法的基本思想是在小波空域相关上实施ICA算法。ICA要解决的问题可以由图1表示。

图1 ICA方法的图解示意
由公式表示为
X(t)=AS(t)
(1)
Y(t)=WX(t)
(2)
以上两式的含义是一组独立的源信号S(t)={si(t);i=1,2,3,…,m},经过一个线性变换网络混合在一起,形成观测信号:
X(t)={xj(t);j=1,2,3,…,n}
式中,信源矢量S(t)和变换网络A都是未知的。
ICA问题是要根据观测信号X(t)分析分离变换网络矩阵W(称为解混矩阵),使得观测信号分离后的矢量Y(t)能够最大程度地再现原信号矢量S(t),也就是说Y(t)各分量接近统计独立。如果假设多个信源信息之间是统计独立的,则通过ICA算法可以将多路混合信号加以分离。
下面给出一种ICA实现算法——信息极大化算法(Info-max算法),该算法是当前较为常用的独立分量分析算法,采用双曲正切函数(tanh)进行累积概率函数逼近,算法如图2所示。
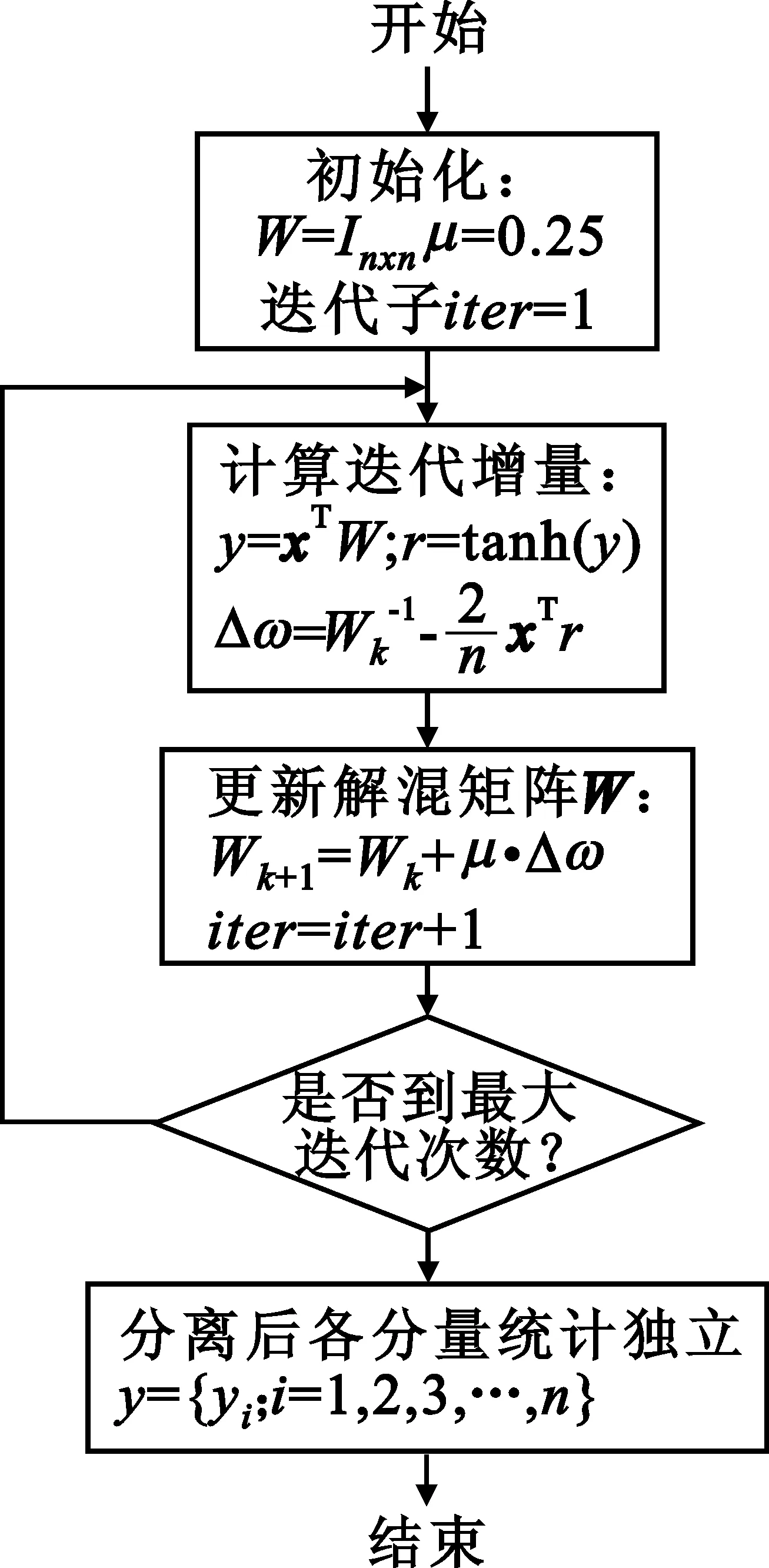
图2 Info-max算法流程
(1)初始化:设定解混矩阵W为n阶单位阵,步进增量系数μ;
(3)更新过程:通过迭代更新方程Wk+1=Wk+μ·Δωk,更新解混矩阵W;
(4)迭代过程判断:迭代过程判断要决定迭代过程是否继续。通过对迭代次数是否达到最大值的判断是简单而有效的方法,可以降低系统实现的复杂程度。但迭代次数判断方法需要一定的先验知识,这与信号统计特征和混合程度有关系。另外一种判断方法是通过计算熵每次的迭代增量来进行判断:
式中,ri=gi(yi)=tanh(yi)。设定ε>0,当ΔH(y)<ε时迭代过程终止。
文献[4,5]给出了小波空域相关的具体算法。对时间离散序列x(n),其小波系数表示为
式中,Ts为采样间隔,j、k分别为尺度和时移因子,ψ为小波函数。小波空域相关系数表示为
式中,l为空域相关深度,通常l=2,则有:
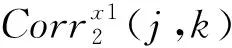
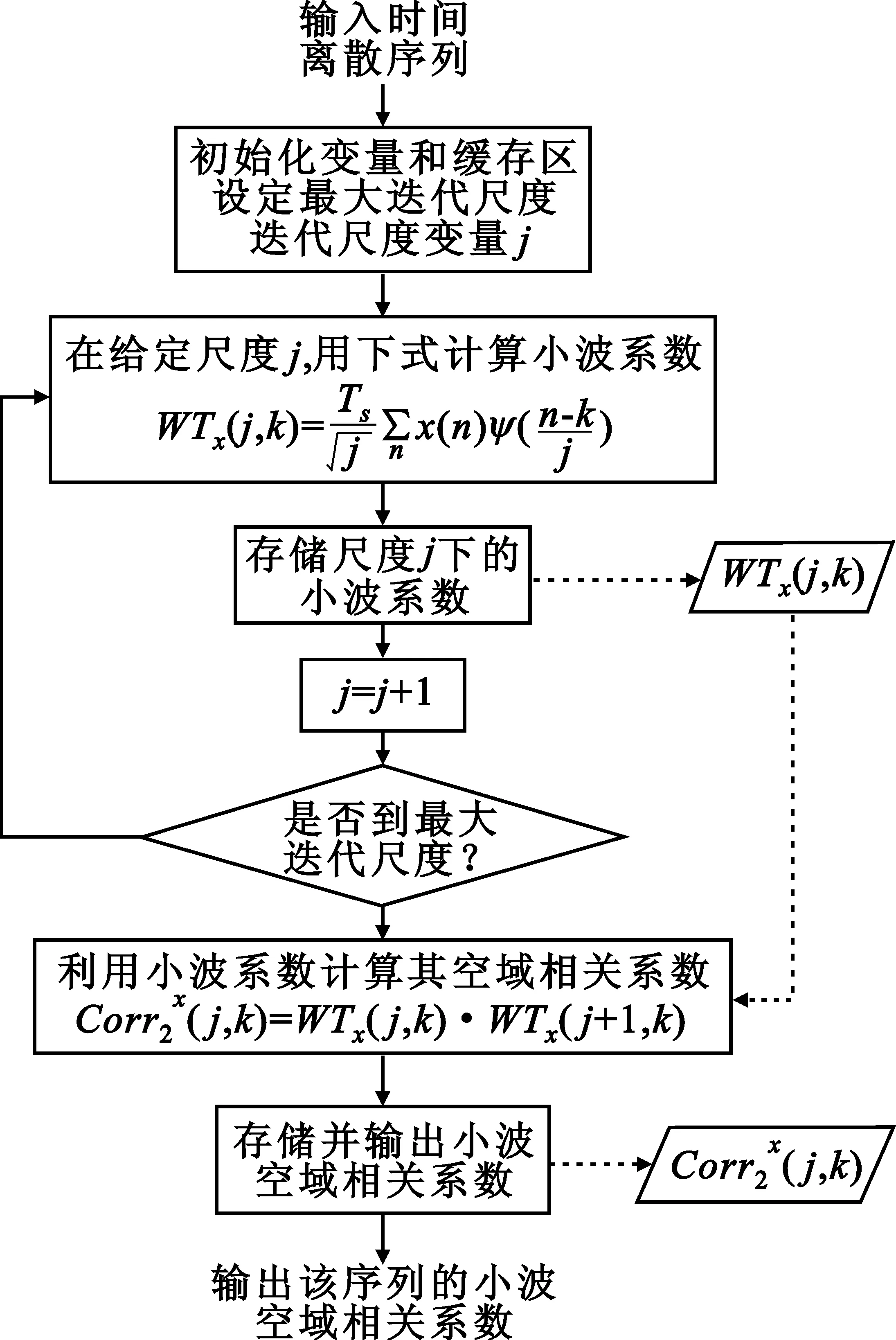
图3 小波空域相关算法流程
小波空域相关ICA完整算法如图4所示。图4表明小波空域相关ICA方法只利用单导信号即可求解解混矩阵,而传统ICA方法则需要多导混合信号才能求解混合矩阵。在某些天线馈源数量小于源信号数量的情况下(超分离问题),本文方法有着重要的意义。

图4 空域相关ICA方法过程
仿真结果表明,信号在小波空域具有很大的峭度[2,4],因而对分离算法有利。
3 在跳频信号盲分离应用中的仿真
仿真试验中设计两个有频点冲突的跳频信号。为便于说明,本文在基带对信号进行仿真。
设信号采样率为fs,某频点频率为f1,产生n个采样点,则在该时段内信号为
s(k)=cos(2πkf1/fs),k=0,1,2,…,n-1
产生两个相互独立的跳频信号s1(k)、s2(k),每个信号4个频点,其中2个频点相同,模拟发生时频冲突的情况。仿真实验中,共存的两个跳频信号跳频间隔为5 kHz,带宽为50 kHz,跳频速率分别为1 000 hop/s和667 hop/s。跳频信号1(FH1)的跳频序列为35 kHz、10 kHz、40 kHz、25 kHz;跳频信号2(FH2)跳频序列为25 kHz、40 kHz、10 kHz、35 kHz、25 kHz、30 kHz、20 kHz。数据采样频率为100 kHz,分析窗口采样点数目N=600,即6 ms长的数据分析窗,因此一个分析窗包含4跳的FH1信号和6跳的FH2信号,SNR=10 dB,如图5所示。

(a)FH1的时域波形

(b)FH2的时域波形
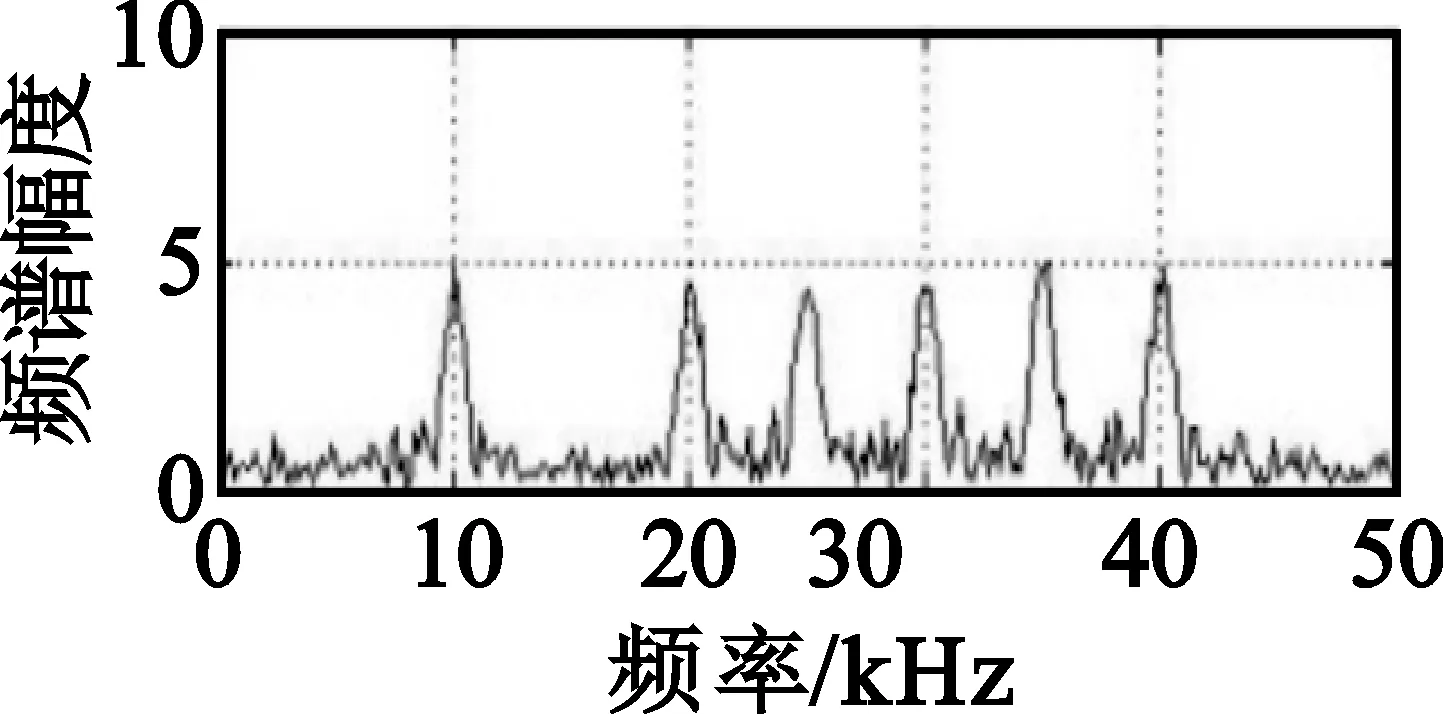
(d)FH2频谱
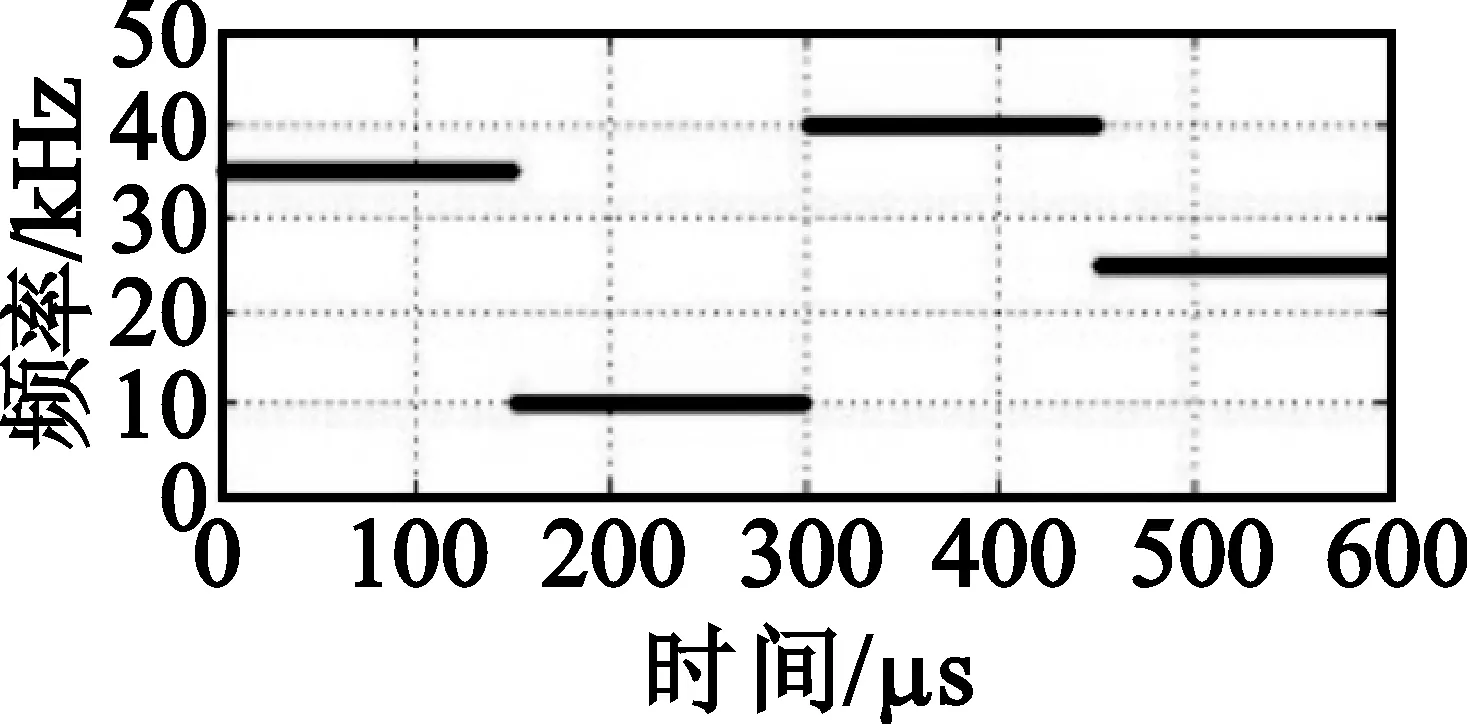
(e)FH1的时频矩阵
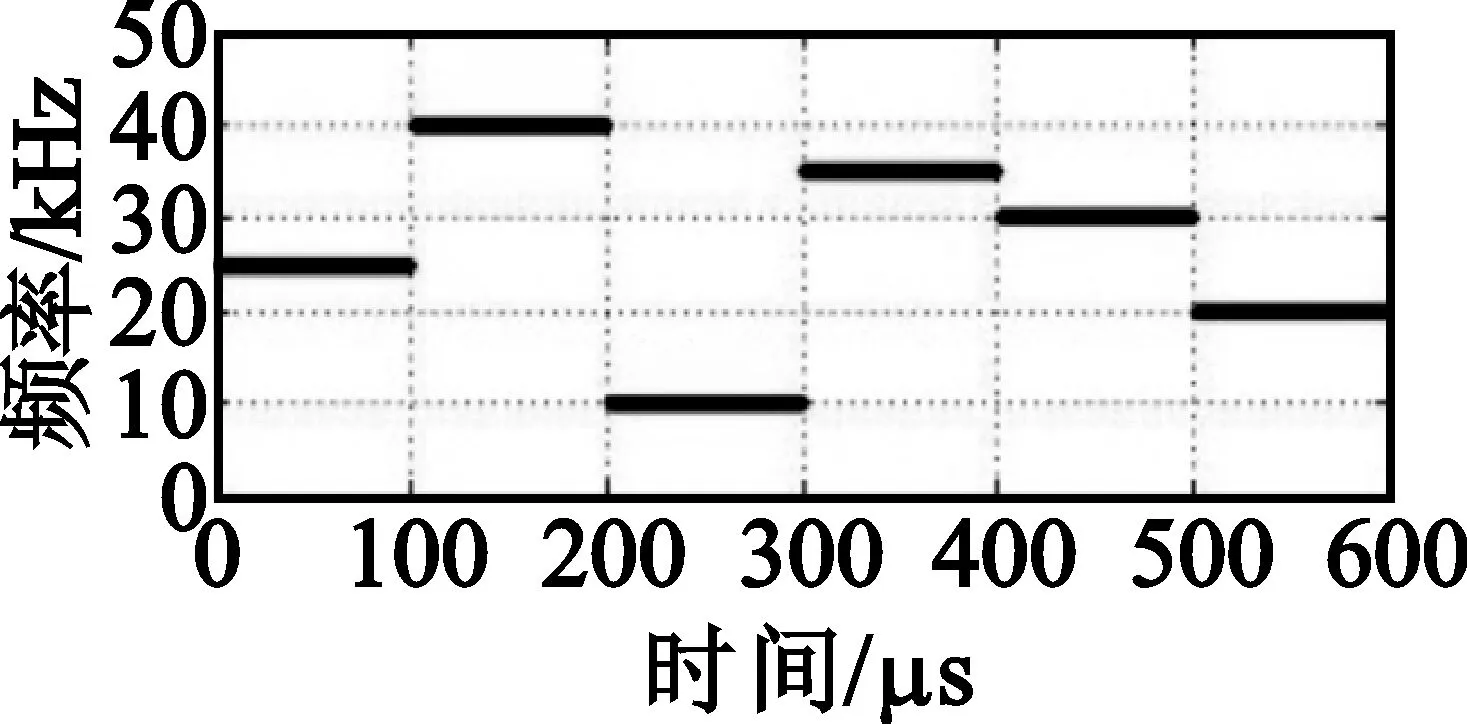
(f)FH2的时频矩阵
可以认为两个跳频信号之间统计独立。假设有两根接收天线,两跳频信号在两天线上有不同的接收强度。这时,信号经过空间传播,在接收端的两个天线馈源形成两导混合信号,相当于加噪的两信号混合。
没有进行信号分离,直接采用小波变换进行参数估计的结果如图6所示,可以看出此时估计出的频率、时间参数以及时频矩阵都与发射端不一样,各分量都互相包含一定强度的其它分量(线性交叉分量),导致对某个跳频信号的小波时频分析出现较大的误差。还注意到,未经分离的信号经过小波变换后时域剖面的频率跳点较为模糊,基本无法分辨出时跳间隔。

(a)混合分量1小波变换(频域)

(b)混合分量2小波变换(频域)
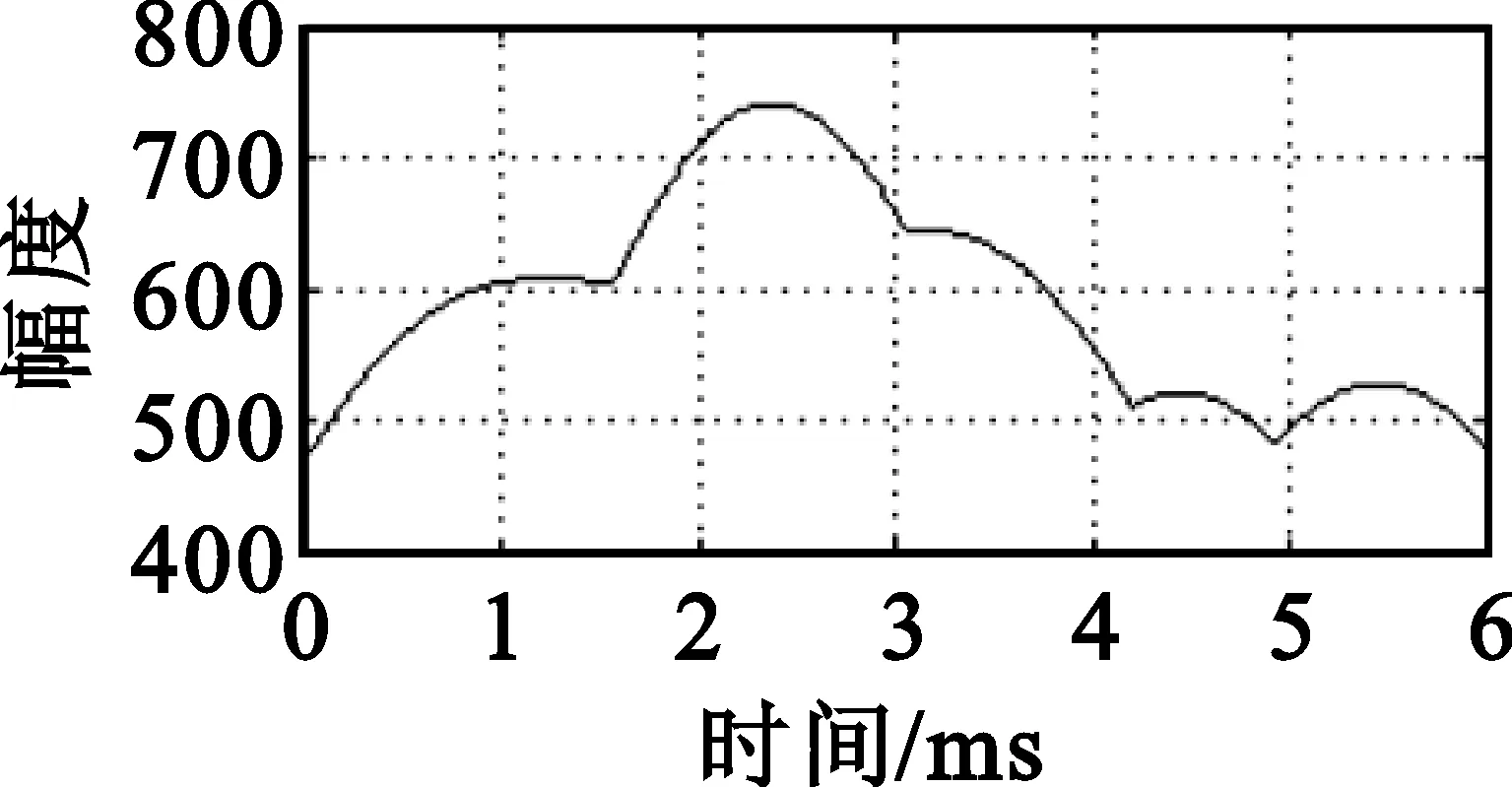
(c)混合分量1小波变换(时域)
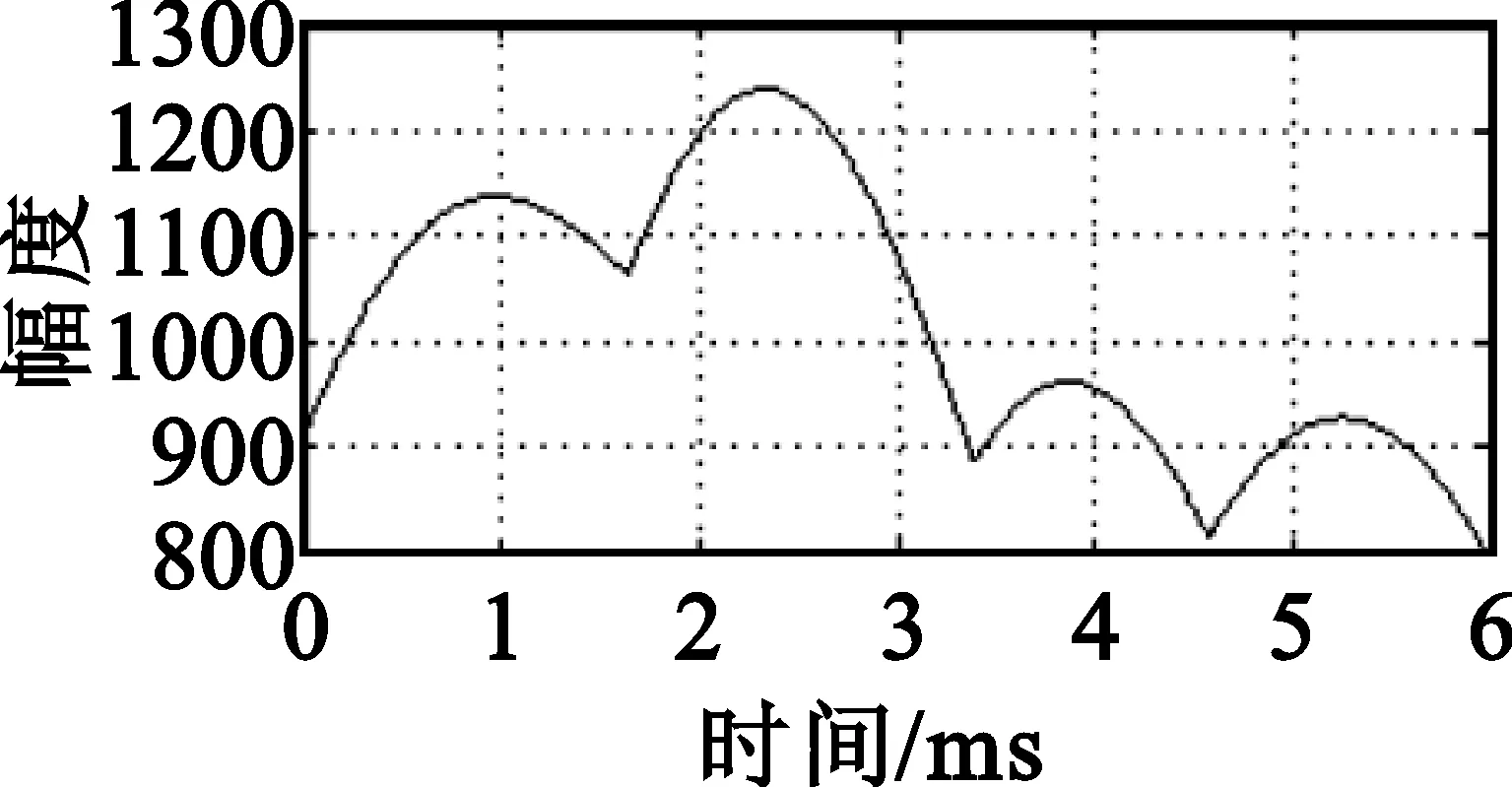
(d)混合分量2小波变换(时域)

(e)混合分量1小波变换(时频域)

(f)混合分量2小波变换(时频域)
经过空域相关ICA盲分离后,再分别进行小波变换得到的两个跳频信号的参数估计值,包括时域、频域和时频矩阵,如图7所示。从频域剖面(图7(a)和图7(b))看,分离后独立分量的频域交叉量得到有效降低。从时域剖面(图7(c)和图7(d))看,分离后两个跳频信号的频率跳点非常清晰,完全可以分辨出时跳间隔,进而提高时跳周期参数估计的准确程度,这一点尤其对跳频信号的参数估计有非常重要的作用。
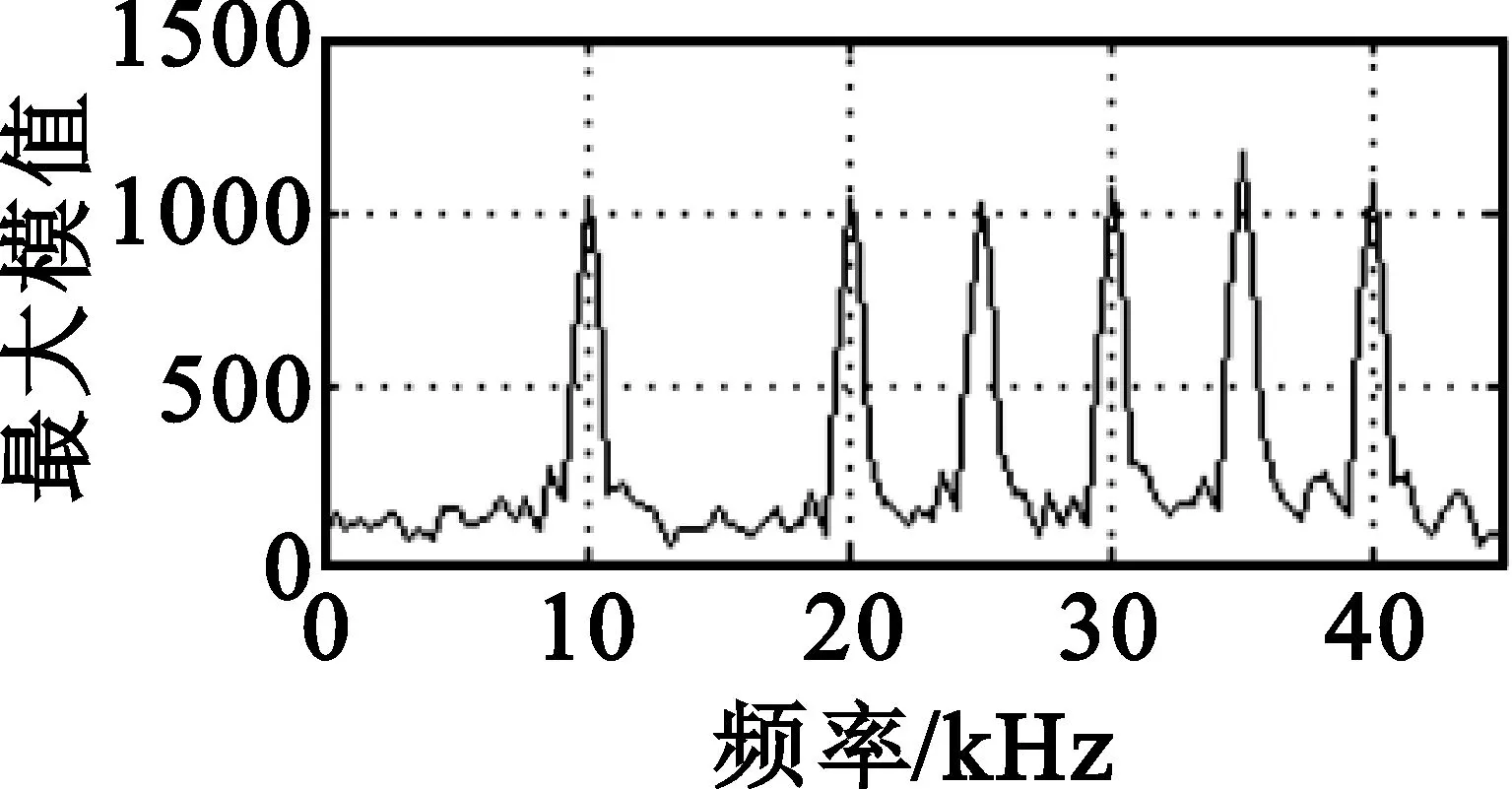
(a)独立分量1小波变换(频域)
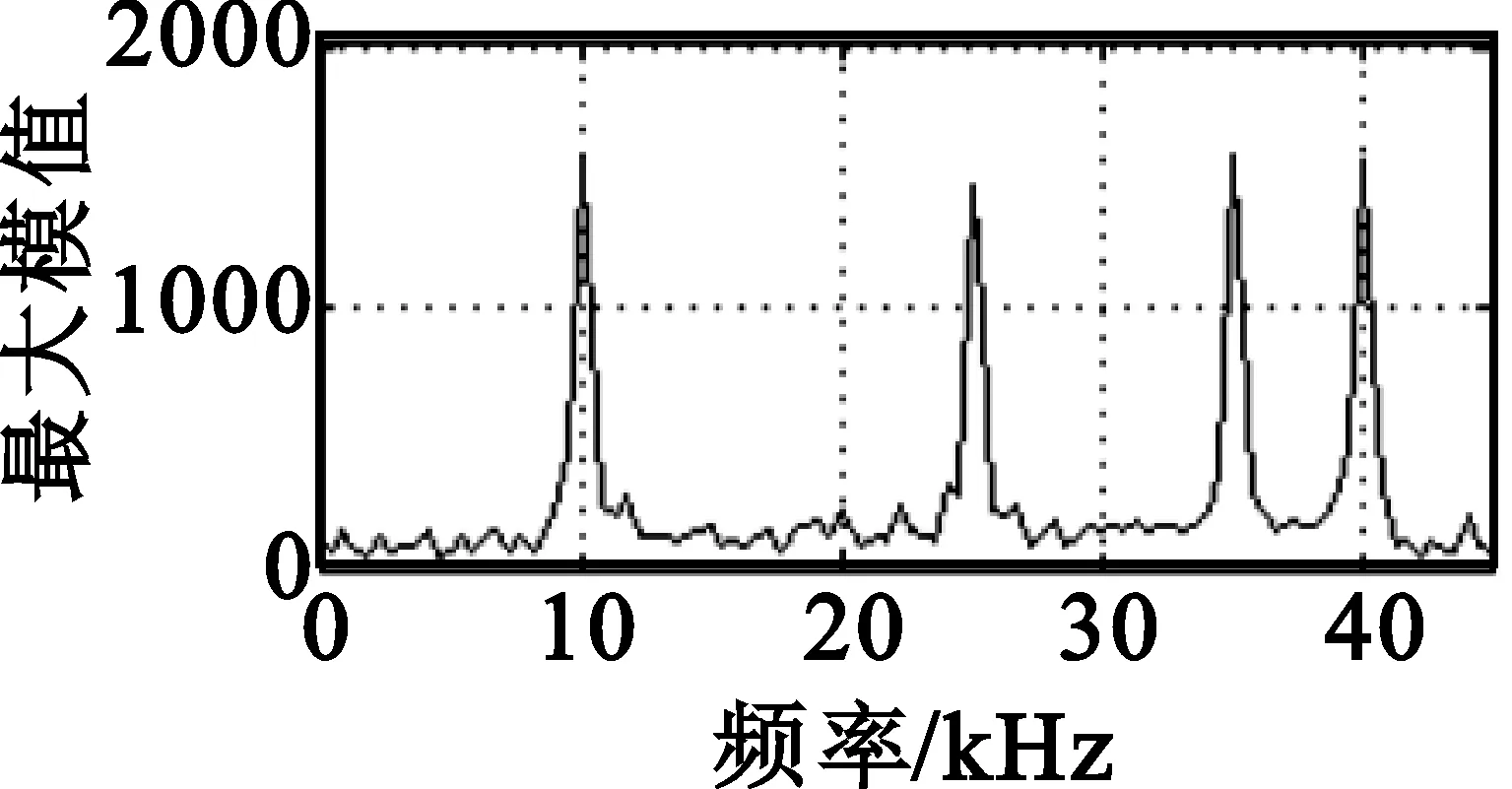
(b)独立分量2小波变换(频域)

(c)独立分量1小波变换(时域)

(d)独立分量2小波变换(时域)

(e)独立分量1小波变换(时频域)

(f)独立分量2小波变换(时频域)
4 性能分析及结论
在实际应用中,源信号的混合程度对ICA算法分离的效果有较大影响。一种极端情况是,各混合分量中所含各原信号强度完全相同,这时ICA算法性能最低。但实际应用中,由于天线在空间分布、天线方向性的差别而导致各天线馈源输出的多导信号所含原信号分量具有较大的差别,因而ICA分离算法还是完全有效的。
从分离的效果看,多天线的数量对多跳信号的有效分离也具有很大的影响。如果设原多跳信号包含n个相互独立的分量信号,则应保证提供给处理机的天线馈源数量不小于n,通常馈源数量取n+1。由于接收信号混合有传播空间的噪声(也认为与原分量信号互相统计独立),因此通过ICA分离算法在一定程度上可以分离出噪声。进一步通过对噪声统计特性的估计,可以有效地用于对分离后的独立分量分别进行降噪处理,进而提高对跳频信号参数估计的准确度和估计精度。
仿真结果表明,小波空域相关ICA方法只利用单导信号即可求解解混矩阵,而传统ICA方法则需要多导混合信号才能求解混合矩阵。在某些天线馈源数量小于源信号数量的情况下(超分离问题),本文方法有着重要的意义。所提出的应用空域相关ICA方法对在时间窗口发生频率碰撞的多跳信号能够显著地分离,从而提高多跳信号参数估计的准确度和精度。
理论和仿真结果表明,利用单导观测信号进行解混矩阵的求解要求混合矩阵A各列之间具有近似的线性关系。另一方面,在更多个不同尺度下利用空域相关系数进行ICA算法最大所能分离的信源数量都将是下一步研究的重点。
参考文献:
[1] 茹乐.军事通信中跳频信号的截获与干扰技术研究[D].西安:空军工程大学, 2007.
RU Le.Research on the Technology of Frequency-Hopping Signal Intercepting and Jamming in the Military Communication[D].Xi′an:Air Force Engineering University,2007.(in Chinese)
[2] Andrzej Cichocki, Shun-ichi Amari.Adaptive Blind Signal and Image Processing[M]. London:John Wiley & Sons, Ltd, 2002.
[3] 杨福生,洪波.独立分量分析的原理与应用[M].北京:清华大学出版社, 2006.
YANG Fu-sheng,HONG Bo.Independent Component Analysis Theory and Application[M].Beijng:Tsinghua University Press,2006.(in Chinese)
[4] Jarari M G. Fetal electrocardiogram extraction by sequential source separation in the wavelet domain[J]. IEEE Transactions on BME, 2005,52(3): 390-400.
[5] Xu Yansun, Weaver J B,Healy D M,et al. Wavelet transforms domain filters: a spatial selective noise filtration technique[J]. IEEE Transactions on Image Processing, 1994,3(6): 747-758.
[6] 潘泉,张磊,孟晋丽,等.小波滤波方法及应用[M].北京:清华大学出版社, 2005.
PAN Quan,ZHANG Lei,MENG Jun-li,et al.Wavelet filtering method and application[M].Beijing:Tsinghua University Press, 2005.(in Chinese)

