削波后的甚低频大气噪声中的通信接收性能*

(海军潜艇学院，山东 青岛 266071)

1 引 言

甚低频(VLF)电磁波传播距离远、隐蔽性好、信号稳定，具有一定海水穿透能力，是各国海军进行海上远距离通信和水下通信的重要手段。影响甚低频通信系统接收性能的主要因素是大气噪声，具体来说是一种高斯白噪声背景下的脉冲噪声。目前对抗大气噪声干扰的一种基本处理方法是在接收机前端对脉冲噪声进行削波处理，即对信号进行时域限幅或对脉冲噪声样本点时域置零[1]。

削波器从20世纪30年代起就开始应用于信号处理，随着甚低频通信的发展，它始终被应用于甚低频通信接收端的噪声滤除。然而，当前关于削波器在甚低频通信中应用的分析和实验结果却十分少。本文首先对削波后的大气噪声成分进行分析，建立削波后的大气噪声模型，接着分析大气噪声中的甚低频通信系统的误码性能和削波器参数对接收误码率的影响，最后对系统性能进行仿真。

2 削波后的大气噪声模型

甚低频频段的大气噪声主要是由雷电瞬时放电引起的，它是高斯白噪声背景下的脉冲噪声。高斯白噪声是由分布于世界范围内的大量雷暴形成的脉冲叠加构成，脉冲噪声是由接收机附近的闪电电磁脉冲叠加形成，脉冲能量极强，持续时间短，噪声能量主要集中在脉冲成分中。据此，可以将大气噪声看作两个独立的随机过程之和[2，3]：

n(t)=w(t)+p(t)

(1)

式中，w(t)为大气噪声中的高斯白噪声成分，均值为0，双边带功率谱密度为N0/2，则：

(2)

p(t)为脉冲噪声成分，可以看成无数个随机产生的窄脉冲之和，用单位冲激函数来表示这些窄脉冲，则p(t)可表示为

(3)

式中，a1，a2，…,am为脉冲的随机振幅，τ1，τ2，…,τm为随机延迟，且随机序列{am}、{τm}与噪声n(t)相互独立。脉冲噪声的特性由随机振幅和随机延迟决定。

甚低频接收机前端通常包含一个非线性部分，例如削波器。当输入信号的幅度较小时对信号的处理是线性的，当信号幅度超过某一个特定值时处理为饱和的。饱和幅度通常设在稍高于信号幅度峰值的某个位置，从而当噪声尖峰产生时出现饱和，并“削去”这些尖峰。非线性削波的模型如图1所示，输出s′(t)由下式给出[1]：

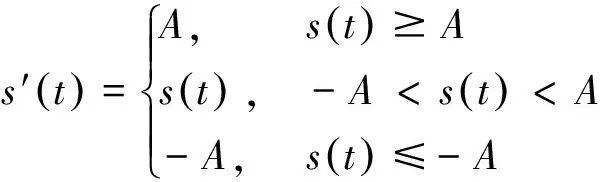
(4)

式中，A为饱和幅度。

图1 削波器模型Fig.1 Model of clipper

脉冲噪声的随机振幅am远大于信号的幅度峰值，经过接收前端的削波处理后，可以认为序列{am}中所有元素的值变为A或-A，即am服从{-A,A}上的等概率伯努利分布。

如果用K(Δ)表示在时间区间[t，t+Δ)上的脉冲到达数，则它可以看作一个服从参数为λv的泊松计数过程：

(5)

式中，k=0,1,2，…；λv表示脉冲到达的速率，它并不是一个定值，这是因为引起脉冲噪声的雷电产生的时间和地点都是随机的，因此对于处于某点位置的接收机来说，脉冲噪声的发生频率是变化的。由上式可知，在[iTb，(i+1)Tb)上有K(Tb)个脉冲到达，以p(t,K(Tb))表示[iTb，(i+1)Tb)上的脉冲噪声成分，则：

(6)

由于脉冲的到来服从泊松分布，可知τ1,…，τK(Tb)在间隔[iTb，(i+1)Tb)内服从均匀分布。

3 接收机误码性能分析

下面以BPSK的相干接收为例，分析大气噪声中的接收机系统性能。

(7)

式中，bi为信号所携带的码元信息，bi∈{-1,1}，fc为信号载波频率，则接收机的接收信号为

r(t)=s(t)+w(t)+p(t)

(8)

接收信号r(t)到达接收机后经相干解调得[4]：

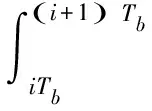
(9)

BPSK相干接收机的积分判决准则为

(10)

假设发送的码元为“1”，即bi=1，通过式(1)、(6)、(7)、(8)可以得到：

(11)

进一步可得到：

(12)

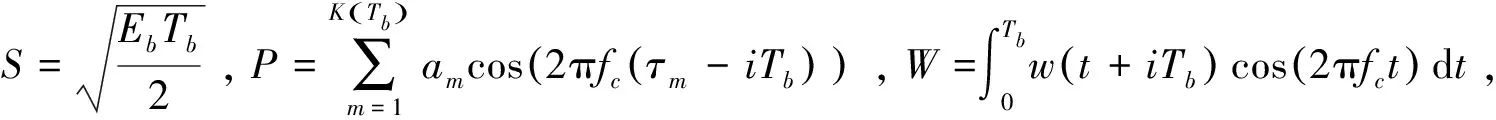
Ri(1)=S+P+W

(13)

(14)

式中,fP(P)为P的概率密度函数。

同理，bi=-1时的误判概率为

(15)

令θm=2πfc(τm-iTb)，则:

(16)

由于τ1,…，τK(Tb)均匀分布于区间[iTb，(i+1)Tb)上，可知θ1，…，θK(Tb)均匀分布于[0,2π)上。又am∈{-1,1}，则可以推出amcosθm的矩量生成函数(Moment Generating Function，MGF)为

Ψamcos θm(jω)=J0(ωA)

(17)

式中，J0(·)为零阶贝塞尔函数，从而P的MGF为

ΨP(jω)=exp (λvTb(J0(ωA)-1))

(18)

因此，P的概率密度分布为

(19)

由式(19)可以看出，fP(P)为偶函数，则综合式(14)、(15)，可令Pe=Pe(1)=Pe(-1)，从而得到：

(20)

将Q(·)在点S/σW进行泰勒级数展开并省略至两项，可得到近似公式:

(21)

式中，第一部分为高斯白噪声存在时的误码率，后半部分则表示由于大气噪声中的脉冲成分导致的性能退化。

4 仿真和分析

为了验证上述结论，使用仿真软件Matlab对甚低频大气噪声中的BPSK通信系统进行蒙特卡罗仿真，仿真流程如图2所示。其中，对于大气噪声中的脉冲成分，通过对λv的设定而生成脉冲的随机到达时间序列，再生成其随机振幅序列，然后合成脉冲噪声，最后与高斯白噪声合成大气噪声，大气噪声的仿真流程图如图3所示。

图2 BPSK接收性能仿真流程图Fig.2 Flow chart of BPSK receiving performance simulation

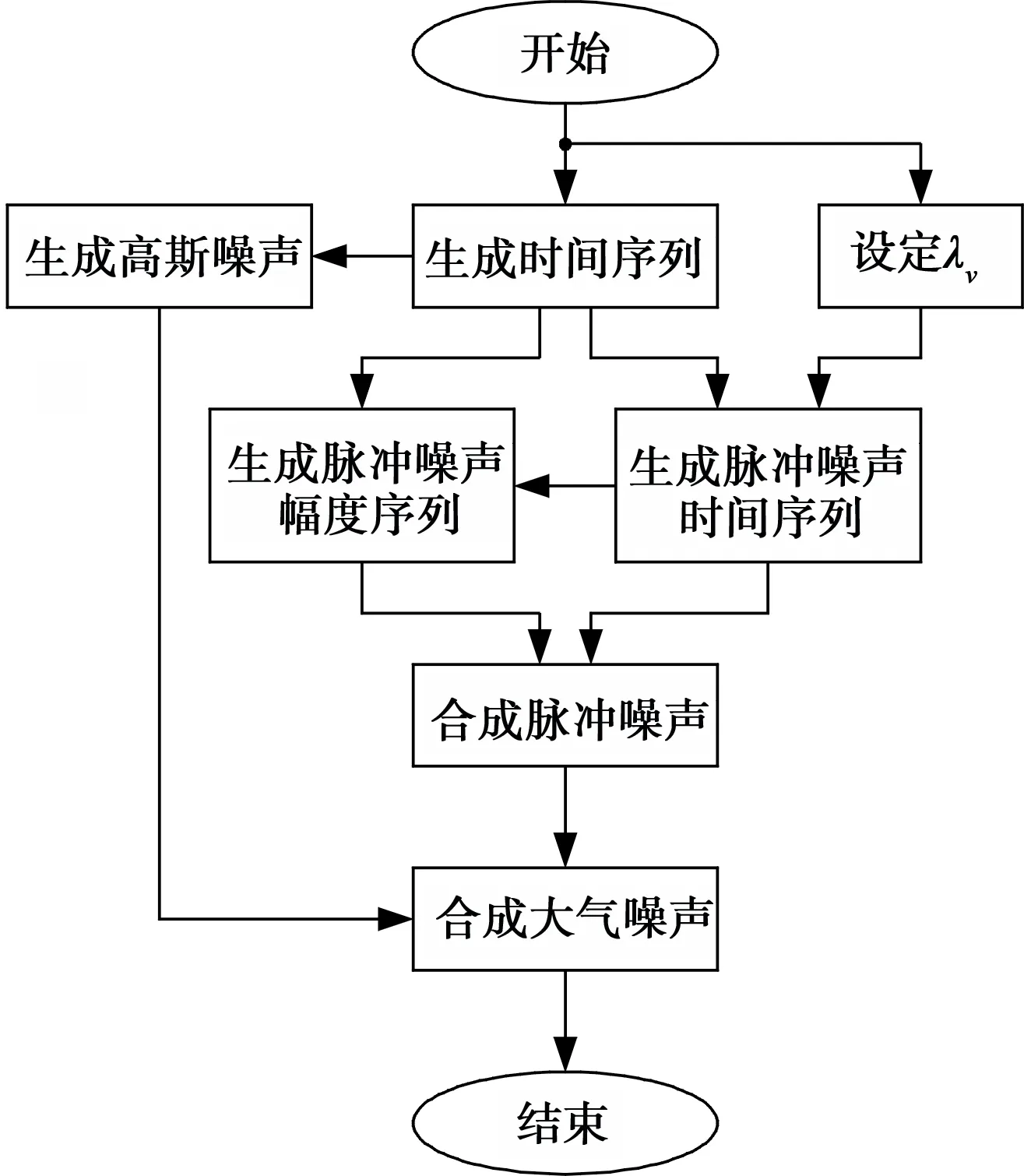
图3 大气噪声仿真流程图Fig.3 Flow chart of atmospheric noise simulation

取λv=10，Tb=0.02，仿真结果如图4所示。可以看出，误码率计算公式能够较近似地计算BPSK相干接收的误码率，但由于在推导过程中对泰勒级数展开式的截取，最后结果存在一定的误差。

图4 误码率仿真结果Fig.4 Simulation results of BER

式(21)中，削波器的饱和幅度以A2的形式出现，表明其对系统的接收性能将有较大的影响，仿真结果也证明了这一点，将A由2变为5，误码率曲线下降的速度变得缓慢，误码率增大。

5 结 论

通过对大气噪声成分的分析，推导出经过削波处理后的噪声模型，与以往的大气噪声模型不同的是，由于削波器的处理，脉冲的随机振幅变为削波器的饱和幅度，大大简化了噪声的仿真。

通过对BPSK相干接收系统的误码性能分析可以看出，削波处理对系统接收性能有较大的改善，且饱和幅度的设定对系统的性能有较大的影响，饱和幅度越高，系统的误码率就越大。

参考文献：

[1] Jim K O,Paul D S.Modem performance in VLF atmospheric noise[J].IEEE Transactions on Communication,1971，19(3):659-668.

[2] 刘玉昌,韩恩权,陈妍.基于MATLAB的VLF/LF通信系统仿真[J].电讯技术,2004，44(5):140-143.

LIU Yu-chang,HAN En-quan,CHEN Yan.VLF/LF Communication System Simulation Based on MATLAB[J].Telecommunication Engineering,2004，44(5):140-143.(in Chinese)

[3] CCIR.World distribution and characteristics of atmospheric radio noise[R]//Report 322-3.Geneva:International Telecommunications Union,1986.

[4] Ranjan K M,Anup K G. An optimum detector for coherent M-ary signaling in the presence of impulsive noise[C]// Proceedings of IEEE International Conference on Person Wireless Communication.[S.l.]:IEEE,2000:363-367.

[5] Adlard J F,Tozer T C,Buur A G.Interference rejection in impulsive noise for VLF communication[C]//Military Communications Conference Proceedings(MILCOM).[S.l.]:IEEE,1999:296-300.

[6] 王小京.超低频信号场强与大气噪声研究[J].舰船电子工程,2009，29(9):79-83.

WANG Xiao-jing.Research on SLF Signal Field Strength and Atmosphere Noise[J].Ship Electronic Engineering,2009，29(9):79-83.(in Chinese)