分数阶傅里叶变换的多项式相位信号DOA估计
(重庆邮电大学 信号与信息处理重庆市重点实验室,重庆 400065)
1 引 言
多项式相位信号(Polynomial Phase Signal,PPS)是信号处理领域中一个具有重要意义的非平稳宽带信号,在通信、雷达、电子对抗、生物医学、声纳、语音等领域有广泛应用。目前,国内外学者大多是针对PPS的相位系数估计进行研究,而对PPS的波达方向(DOA)估计方面的研究甚少。在现代电子通信领域中,精确估计PPS的DOA,实现超分辨测向显得非常重要。线性调频信号(LFM,又称chirp)是PPS的一个特例。当前,LFM信号DOA估计经典的方法有MUSIC、ESPRIT算法等,后来对MUSIC算法提出了一系列改进算法,如求根MUSIC算法[1]、循环MUSIC算法、时频MUSIC算法等,但这些算法都是针对窄带LFM信号的。对于宽带LFM信号,国内学者陶然、齐林等对分数阶Fourier变换(FRFT)的宽带LFM的DOA估计[2]进行了深入研究,并取得了较好的效果;郑州大学的张艳红提出了基于分数阶Fourier变换的宽带LFM信号DOA估计[3],但是针对大于二阶的多项式相位信号,相关的研究却很少。
2 线性调频信号的阵列模型
阵列模型为M个阵元的均匀线阵(ULA),阵元间距为d,如图1所示。假设有一LFM信号s(t),入射角为θ。如果把第一个阵元作为参考阵元,则第i个阵元上的观测信号可以表示为
xi(t)=st-τi+nit,i=1,2,3,…,M
(1)
其中:
τi=i-1dsinθ/c
(2)
st=Aej2πf0t+πKt2+φ
(3)
式中,f0、K和φ分别为LFM信号的初始频率、调频斜率和初始相位,ni(t)为第i个阵元相互独立且与信号无关的高斯白噪声,τi是信号s(t)在第i个阵元相对于第一个阵元的延时,c为光速。
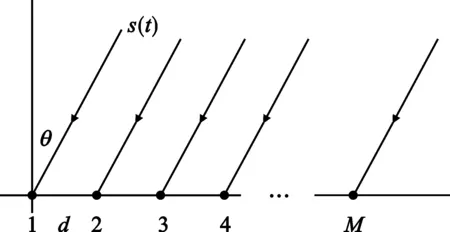
图1 均匀线阵结构示意图Fig.1 The ULA and array model
3 FRFT的DOA估计
3.1 多项式相位变换实现对PPS的降阶
我们考虑多项式相位采样信号模型为
x(n)=s(n)+w(n)=
(4)
式中,0≤n≤N-1,N为采样点数,Δ为采样间隔,am(m=1,2,3,…,M)为PPS的相位系数,M和b0分别为PPS的阶数和幅度,w(n)为均值为零、方差为σ2的高斯白噪声。对于上式的信号模型,τ为延时参数,假设τ和M为正整数。
PPS的一个重要性质就是通过高阶瞬态距(HIM)计算,可得如下信号形式[4]:
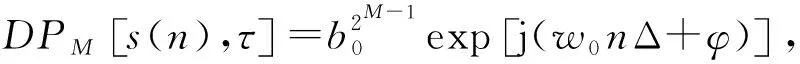
(5)
其中:
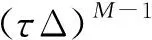
(6)
φ=(M-1)!(τΔ)M-1aM-1-
0.5(M-1)M!(τΔ)MaM
(7)
M阶多项式相位变换定义为DPM[s(n),τ]的离散时间傅氏变换,对一个振幅恒定的M阶PPS应用M阶算子DPM将该信号变换成单个正弦信号,且其频率w0与最高次项系数aM有关。
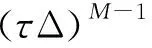
(8)
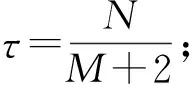
3.2 FRFT实现对LFM信号阵列的窄带化处理
信号x(t)的FRFT定义为[6]
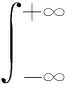
(9)
式中,FRFT的变换核Kp(t,u)为
(10)
式中,n为整数,α称为旋转角度,且α=pπ/2,p为FRFT的阶数,Fp·为FRFT的算子符号,δt为单位冲激函数。
信号xt的FRFT是线性变换,它和Wigner-Ville分布(简称WVD)的关系可解释为时频平面的旋转算子,这一特性决定了FRFT特别适合于处理LFM类信号。如图2所示,与该斜直线相垂直的分数阶Fourier域(FRF域)上求信号的FRFT,则在该域的某点将出现明显的峰值。而噪声的能量均匀地分布在整个时频平面内,在任何的FRF域上均不会出现能量聚集。因此,FRFT在某个FRF域中对给定的LFM信号具有最好的能量聚集[6]。
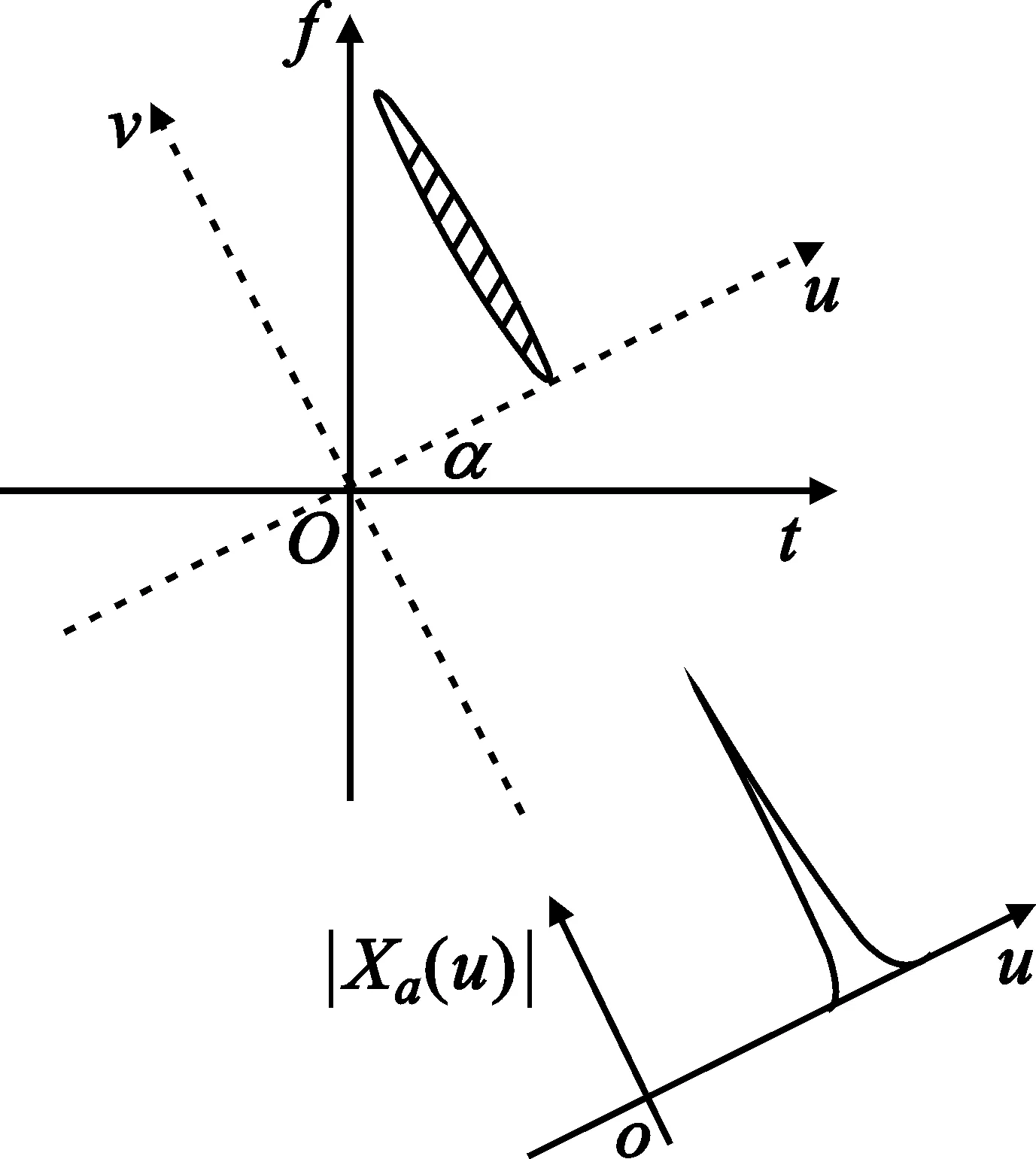
图2 LFM信号的时频分布及其在FRF域上的投影Fig.2 LFM signal in the time-frequency distribution and projection of FRF domain
对信号st进行p阶FRFT,在α,u平面上,运用分级计算迭代搜索方法对spu进行峰值点的二维搜索,即确定分数阶的搜索范围a,b,确定初始步长Δp1=0.1,估计出分数阶的初始值为p1;再进行二次搜索范围p1-0.1,p1+0.1,确定初始步长Δp2=0.01,估计出分数阶的初始值为p2;再进行三次搜索范围p2-0.01,p2+0.01,确定初始步长Δp3=0.001,直至达到所要求的精度。得到峰值点的位置αq和um,则可得信号的调频斜率和初始频率估计[6]:
(11)
也就是说,当旋转角度α=-arccotK时,spu有最佳的能量聚集。
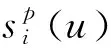
(12)
式中,i=1,2,3,…,M。
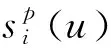
Ap=1,e-j2πτ2u1msinα,…,e-j2πτMu1msinαT
(13)
因此,可得到天线阵列的观测信号在FRF域矢量表达式:
Xp=Apsp+Np
(14)
其中:
(15)
(16)
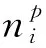
3.3 求根MUSIC算法实现对信号DOA估计
式(14)中的矢量表达式的协方差矩阵为
(17)
式中,Rps和Rpn分别为信号和噪声协方差矩阵。对上式协方差矩阵进行特征分解,可得λ1>λ2>,…,λQ>λQ+1=λQ+2=…,λm,其中,Q为信号源个数,则信号子空间是由大特征值对应的特征矢量组成的空间,而噪声子空间是由小特征值对应的特征矢量组成的空间。
首先定义如下一个多项式[7]
(18)
式中,ei是数据协方差矩阵中小特征值对应的M-Q个特征矢量,pz=1,z,…,zM-1T。
由以上的定义可知:当z=ejw,即多项式的根正好位于单位圆上时,p(ejw)是一个空间频率为w的导向矢量。由特征结构类算法可知,p(ejw)=p(z)就是信号的导向矢量,所以其与噪声子空间是正交的。因此,多项式可定义为
(19)
因为多项式fz的阶数为2M-1,所以有M-1对根,且每对根是相互共轭的关系。在这M-1对根中有Q个根z1,z2,…,zQ正好分布在单位圆上,即:
zi=expjwi,1≤i≤Q
(20)
上式考虑的是数据协方差矩阵精确可知时的情况,在实际应用中也就是数据矩阵存在误差时,只需求式(19)的Q个接近于单位圆上的根即可。也就是对于等距均匀线阵,根据方向导向矢量Ap可知波达方向
(21)
由以上分析,可总结PPS波达方向估计的算法流程:
(1)初始化,令m=M和xmn=xn,其中,0≤n≤N-1;
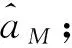
(3)令
(22)
其中,0≤n≤N-1;
(4)替换m=m-1,直到m=2为止;
(5)对信号xmn进行P阶的FRFT;
(6)在相应的分数阶Fourier域,进行峰值搜索,根据旋转角度α不变和式(12),可确定峰值点的位置;
(7)由式(13)、(14)、(15)确定信号在FRF域所对应的方向向量;
(8)利用求根MUSIC算法进行DOA估计,估计最终信号的波达方向。
4 仿真实验
4.1 实验一
设信号模型为
xn=sn+wn=
b0expja1n+a2n2+a3n3+wn
(23)
式中,0≤n≤N-1,a1=0.125,a2=0.25/N,a3=0.65/N2,采样点N=360,延时τ=N/3,离散FFT时变换的长度为120×100点。
图3给出了本文PPS分别在没有噪声和SNR=20 dB时,瞬态矩后的信号实部幅值特性图。从图中可以看出,经过瞬态矩后,没有噪声时,信号为正弦信号;当SNR=20 dB时,信号为正弦信号和新的噪声。图4给出了SNR=20 dB时,经过多项式相位变换的谱线分析,从中可以得到该信号的频率,也就是可以得到三阶PPS的最高阶相位系数a3。图5给出了均方误差(MSE) 随信噪比(SNR)变化的曲线图,从图中可以看出,三阶PPS在SNR≥6 dB时,该方法的估计性能接近克拉美罗界(CRB),而随着信噪比的降低,仿真结果与理论结果产生较大偏差。
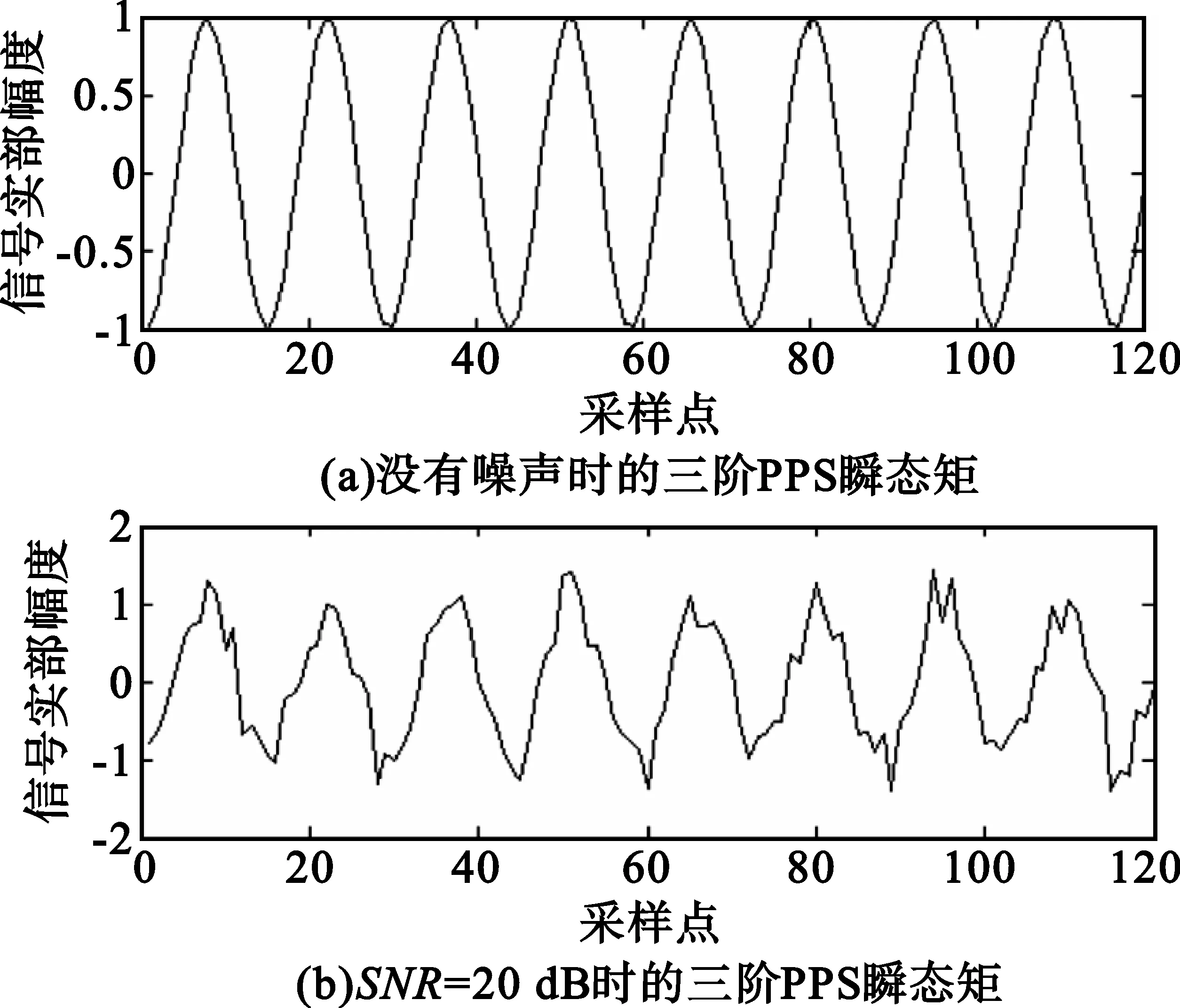
图3 三阶PPS的瞬态矩Fig.3 Instantaneous moment of the third order PPS
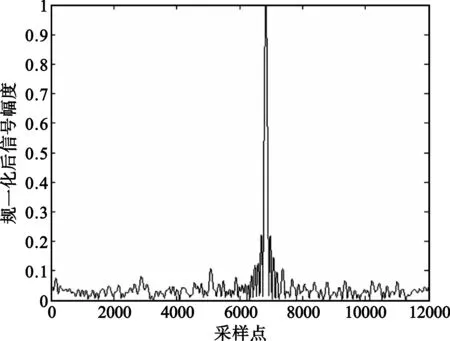
图4 SNR=20 dB时的多项式相位变换谱线图Fig.4 Spectrum of polynomial phase transform when SNR=20 dB
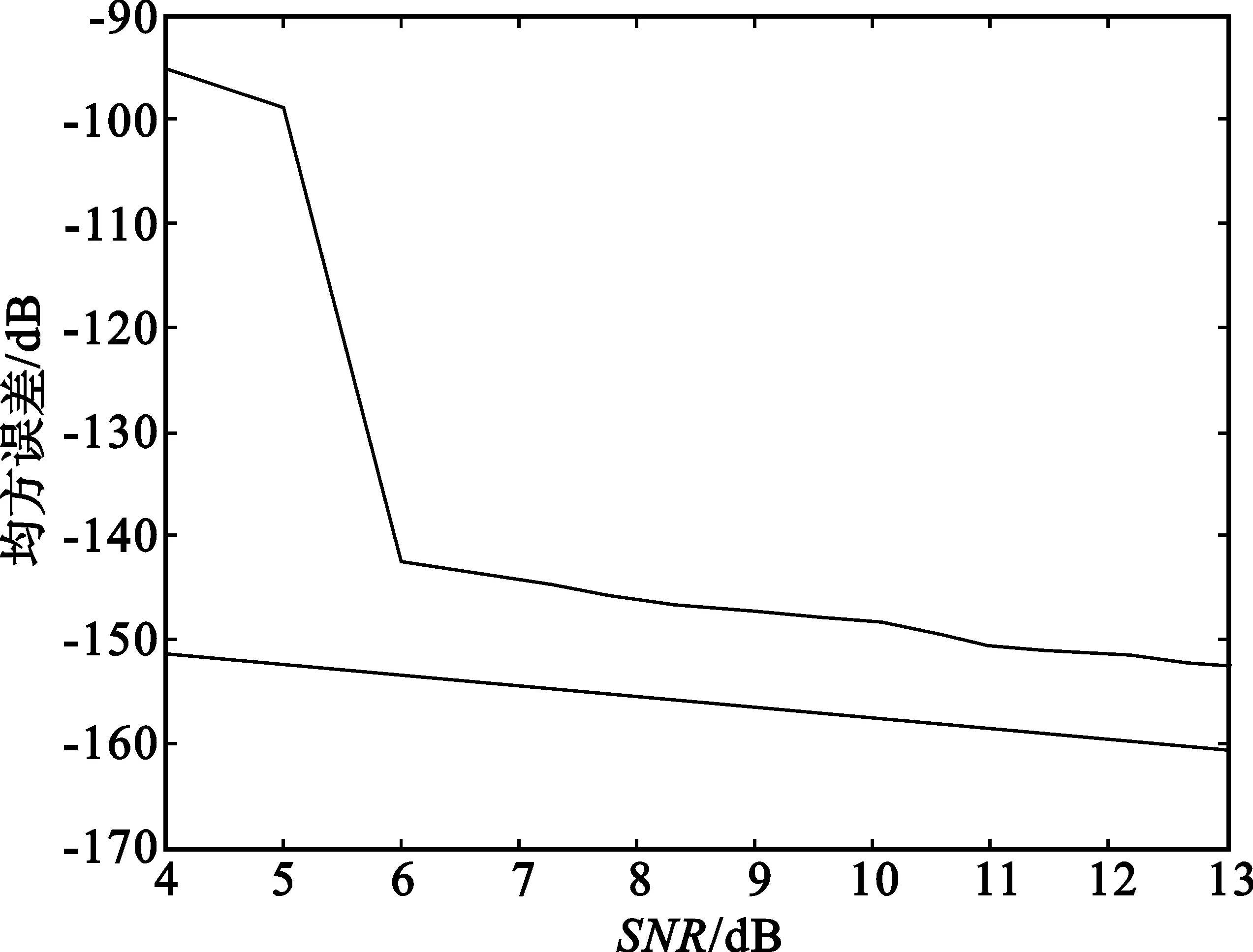
图5 a3估计值均方误差和CRB随信噪比变化图Fig.5 MSE and CRB of a3 versus SNR
4.2 实验二
在实验一的基础上,结合本文提出算法中的第三步降阶的思想,设和实验一有相同的参数,且入射角θ=70°,快拍数为τ。
图6给出了SNR=10 dB时,PPS按本文提出的思想降阶后的FRFT。从图中可以看出,该信号具有很好的能量聚集性,从而把宽带的PPS转化为FRF域窄带信号。在相应的FRF域,用MUSIC算法,对信号进行波达方向估计,如图7所示,从图中可以看出,能较为准确地估计信号的波达方向。图8给出了阵元数分别为10和6时,多项式相位变换结合FRFT的求根MUSIC算法的DOA估计均方误差随信噪比变化的曲线图,从图中可以看出,均方误差随SNR的减小而增加,在SNR>7 dB时,能较为准确地估计PPS的DOA,同时,在SNR相同时,阵元数为10比阵元数为6的估计性能要稍好些。
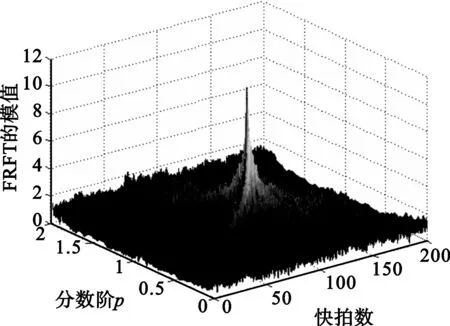
图6 PPS降阶后分数阶Fourier域的信号Fig.6 PPS of order lowered in FRF domain
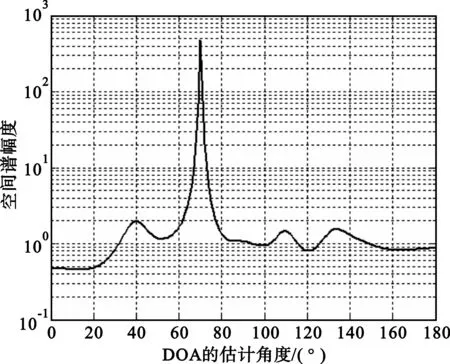
图7 基于FRFT的PPS的DOA估计Fig.7 DOA estimation of PPS based on FRFT
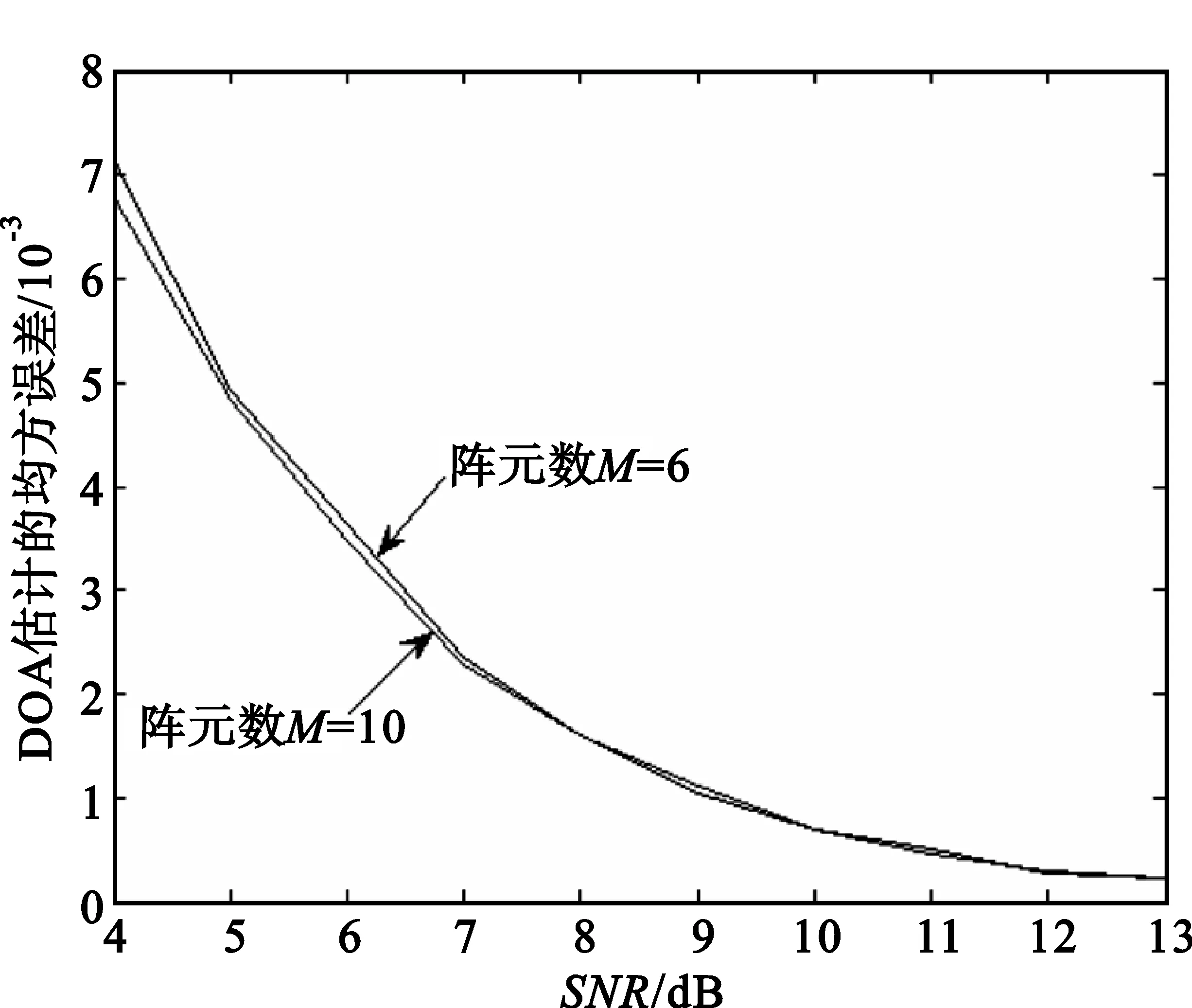
图8 阵元不同时DOA估计随SNR的变化图Fig.8 DOA estimation of different sensors versus SNR
5 结 论
本文提出了一种多项式相位信号波达方向估计的方法,目前有关PPS的DOA估计的文献很少,所以本文为以后在这方面的深入研究打下了一定的基础。由于运用了多项式相位变换降阶,在SNR≥7 dB时能很好地估计出单分量PPS的DOA,但估计多分量的PPS的DOA问题还有待解决。同时,利用分级计算迭代搜索方法对FRF域的峰值点进行二维搜索,计算量大大减小,所以该算法简单。
参考文献:
[1] Barbell A J. Improving the resolution performance of eigenstructure-based direction finding algorithms[C]// Proceedings of IEEE International Acousties, Speech, and Signal Processing Conference.Boston,USA:IEEE,1984:336-339.
[2] 陶然,周云松.基于分数阶傅里叶变换的宽带LFM信号波达方向估计新算法[J].北京理工大学学报,2005,25(10):895-899.
TAO Ran, ZHOU Yun-song. A Novel Method for Direction of Arrival Estimation of Wideband Linear Frequency Modulated Sources Based on Fractional Fourier Transform[J]. Journal of Beijing Institute of Technology, 2005,25(10):895-899. (in Chinese)
[3] 张艳红,齐林,穆晓敏,等.基于分数阶傅里叶变换的WLFM信号DOA估计[J].信号处理,2005,21(4):57-60.
ZHANG Yan-hong,QI Lin,MU Xiao-min,et al.DOA estimation of WLFM signal based on fractional Fourier transforms [J].Signal Processing,2005,21(4):57-60.(in Chinese)
[4] Peleg S,Porat B. Estimation and Classification of Polynomial-Phase Signals[J]. IEEE Transactions on Information Theory, 1991,37(2):422-430.
[5] Peleg S,Friedlander B. The discrete polynomial phase transform[J].IEEE Transactions on Signal Processing, 1995, 43(8):1901-1914.
[6] 陶然,齐林,王越.分数阶Fourier变换的原理与应用[M].北京:清华大学出版社,2004.
TAO Ran, QI Lin, WANG Yue. Fractional Fourier Transform and Its Applications[M]. Beijing:Tsinghua University Press, 2004. (in Chinese)
[7] 万军,束坤.求根MUSIC算法与四阶MUSIC算法的分析比较[J].舰船电子对抗,2008,31(4):97-101.
WAN Jun, SHU Kun. Analysis and Comparison between Root-MUSIC Algorithm and Furth-order MUSIC Algorithm [J].Shipboard Electronic Countermeasure,2008,31(4):97-101. (in Chinese)

