两种不同计算发射截面方法的比较
刘永皓,董云峰,刘彰基
(1.大庆师范学院 物理与电气信息工程学院,黑龙江 大庆 163712;2.大庆师范学院 人力资源部,黑龙江 大庆 163712)
0 引言
光谱学常用吸收和发射截面来表示吸收和发射几率。截面具有面积的量纲,它与光束面积的比表示一个吸收或发射中心(原子或分子)吸收或发射光辐射的几率。发射截面是评估材料的阈值和斜率效率的重要光谱参数,其具体数值可以从激光器件参数的测试中得到,也可以通过自发辐射的荧光光谱测试中得到。本文根据与时间有关的微扰理论[1]及Judd-Ofelt理论[2]分别对两种方法进行了比较,并指出了其各自的适用范围。
1 光谱理论
在介质材料中,电偶极跃迁的受激辐射和自发辐射几率分别为
(1)
(2)
常用的表示式中一般以光场能量密度d(ωk)或光强I(ωk)来表示光子数nk,即
从而
(3)
将式(3)代入式(1)可得
(4)
如果引入光强I(ωk)=(c/n)d(ωk),那么式(4)就变成
(5)
2 主要结果
2.1 倒易法(McCumber理论)[4-6]——由吸收光谱计算发射截面
光沿着x方向通过一个二能级系统的介质。N2和N1分别是其高、低能级的单位体积粒子数,g2和g1为简并度。用Pk(1n,2m)表示能级1的第n个简并态到能级2的第m个简并态的跃迁几率(相应的,用Pk(2m,1n)表示能级2的第m个简并态到能级1的第n个简并态的跃迁几率)。显然,粒子在能级1是处于g1个简并状态中的某一个状态中,但是它跃迁到能级2,我们并不限定它只能处在g2个简并状态中的那一个状态。这就是在求从能级1到能级2的跃迁总几率时,应该对终态能级2的各个简并态求和并对能级1的各简并态平均的根据,因此
(6)
相似地,由能级2向能级1跃迁的总几率应为
(7)
由于PK(2m,1n)=PK(1n,2m),从而有
g1W12=g2W21
(8)
通过dx厚度的介质后由于光被介质吸收,光束的强度减弱,其强度变化为

=-k(ωk)I(ωk)dx
(9)
上式引入gL(ωk)这一线型因子以便计入吸收谱线的线型,并且已考虑到激发态上的粒子数远远小于基态的粒子数从而忽略去g1N2/g2。由此可以得到光通过厚度为x的介质后光强度表示式
I(ωk)=I0(ωk)e-k(ωk)x
(10)
显然k(ωk)就是吸收系数
(11)
如果用波长作变数,由于
其中


(12)
则
(13)
上面的讨论有一个前提,就是光的强度足够大,从上能级到下能级的自发辐射相比之下可以忽略,并没有考虑到伴有声子产生的光发射和声子湮灭的光吸收的不等价产生的误差。吸收系数除以吸收中心的数目就是吸收截面。因此,以圆频率和波长为变数的吸收截面σ(ωk)和σ(λk)可以分别表示为
(14)
(15)
(16)
发射截面实际上指的是受激发射截面,它是直接与激光器件参数联系的一个光谱参数,它可以从激光器件参数的测试中得到,又可以从自发辐射的荧光光谱测试中得到:

=a(ωk)I(ωk)dx
(17)
I(ωk)=I0(ωk)ea(ωk)x
(18)
在这一计算中同样忽略了自发辐射
从式(17)可得光放大系数
从而受激发射截面

(19)
σ21=g1σ21/g2
(20)
σji=giσij/gj
上面是针对两个窄能级给出的,材料中发光和吸收往往发生于由多个具有一定简并度的子能级组成的高低能级之间的跃迁,离子在高低能级各个子能级中按玻尔兹曼分布律分布,电子与晶格耦合使某一频率的发光或吸收可能来自不同的子能级对,计算吸收截面和发射截面必须是各个子能级相关值的代权平均,权重因子对高能级用gje-εj/kT,低能级用gje-εj/kT,发射截面和吸收截面成为:
εj和εi是从各个多重态的“底部”算起的能量,Ej,Ei是从基态算起的能量,定义式如下:
εj=Ej-EZL,εi=Ei,Ej-Ei=ħω,εj-εi=ħω-EZL
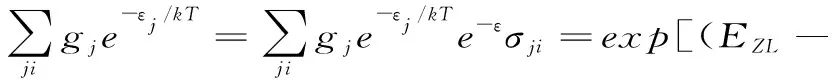
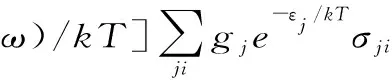
因此,吸收截面和发射截面的交互性关系变成

(21)
式中EZL是高低能级组最低子能级的能量差,高低能级组对应的Zu和Zl都可由下式求出
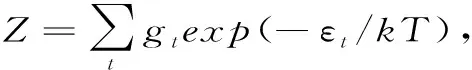
(22)
此即从吸收截面计算发射截面经常用到的倒易法公式。
因此,利用倒易法,只要知道样品的吸收截面和激活离子的能级图就可以得出受激发射截面。然而,倒易法只能用来计算吸收和发射过程属于同一对多重态的情况,而对于目前广泛研究的Nd3+离子4F3/2→4I11/2的跃迁,由于能级4I11/2到能级4F3/2吸收谱测量困难,它就无能为力了。对Yb3+离子,由于辐射陷阱效应的影响,荧光谱变形比较严重,所以采用倒易法更能真实反映真实荧光谱。
2.2 Fuchtbauer-Ladenburg公式(简称F-L公式)[7] ——由荧光光谱计算发射截面
由式(2)可知,对于具有一定简并度的两个能级1和2之间的跃迁,其几率为
(23)
同式(19)比较,显然有
(24)
在这里受激辐射的参数(受激发射截面)和自发辐射的参数(自发辐射几率)联系起来了,这是由于不论是受激辐射还是自发辐射都来源于相同的跃迁机制-电偶极跃迁,其跃迁几率都正比于相同的跃迁矩阵元的平方,唯一的不同只是受激辐射的跃迁几率表示式中多了一个因子-辐射场强度。这是用荧光光谱计算受激发射截面的物理基础。
(25)
其中式(25)是对两个特定的晶场能级之间跃迁的发射截面, A21是上能级到终多重态的一个特定晶场能级的自发辐射跃迁几率,如果要与J-O三参数方法计算出的辐射寿命相联系,并表示成

β2是波长为λ的荧光跃迁几率与两个多重态之间的自发辐射几率比
(26)
(27)
(28)
另外,式(28)也可通过以下思路得到:
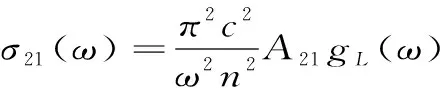
(29)
假定荧光探测系统的灵敏度是G,多重态的总离子数是Nu,则波长为λ的荧光总强度可以表示成:
(30)
对于两个多重态之间的整个荧光谱,它发射的光子总数为
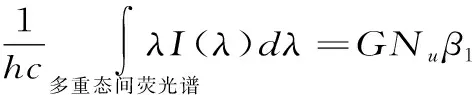

(31)
此时,将相应式子代入(31)式,得到与(28)式相同的表示式
在利用F-L公式计算某个波长的发射截面时,需要利用测量的荧光谱。如果由于某些原因,比如存在辐射陷阱效应、仪器测量误差等,无法通过测量得到样品准确的荧光谱,那么利用上述方法计算出的发射截面就会有较大的误差。
3 结论
McCumber理论和F-L公式这两种方法都可以用来计算稀土离子从激发态向基态跃迁的发射截面。McCumber 理论是从离子的吸收光谱计算发射截面,而吸收光谱的测量技术已很成熟。但在应用这种方法时,必须知道离子在基质材料中的能级结构,给这一方法的应用造成了困难。用F-L 公式计算发射截面时需要测量归一化谱线函数,当离子存在对荧光的自吸收效应时,要准确测量归一化谱线函数是很困难的。总之,对于Yb3+等辐射陷阱效应影响较大的离子,采用倒易法更能真实反映真实荧光谱;对于吸收和发射过程属于同一对多重态的情况,如目前广泛研究的Nd3+离子4F3/2→4I11/2的跃迁,由于能级4I11/2到能级4F3/2吸收谱测量困难,采用F-L公式则更加合适。
[参考文献]
[1] Heitler W. The Quantum Theory of Radiation[M]. Oxford: Clarendon Press, 1954.
[2] Judd B. R. Optical absorption intensities of rare-earth ions[J]. Phys. Rev., 1962,127: 750-761.
[3] Ofelt G. S. Intensities of crystal spectra of rare-earth ions[J]. J. Chem. Phys., 1962,37: 511-520.
[4] McCumber D. E. Einstein relations connecting broadband emission and absorption spectra[J]. Phys. Rev. 1964,136: A954-957.
[5] 罗遵度,黄艺东. 固体激光材料光谱物理学[M].福州:福建科学技术出版社,2003:55-76.
[6] Miniscalco W. J., Quimby R. S. General procedure for the analysis of Er3+ cross sections[J]. Opt. Lett. 1991,16: 258-260.
[7] 干福熹,邓佩珍.激光材料[M].上海:上海人民出版社,1976:356-360.

