一类特殊的交错矩阵几何

肖 旭

(长沙理工大学 数学与计算科学学院，湖南 长沙 410004)

0 引言

矩阵几何是我国著名数学家华罗庚于20世纪40年代中期由于研究多复变函数的需要而开创的一个数学领域，它实际上将空间中的一个点看成为某一类矩阵的集合，而且有一个变换群作用在这个空间上，其基本思想是研究保持某一性质或几类性质不变的变换群的形式，即矩阵几何的基本定理，而研究这一形式时又是从空间中的点与点之间的距离与算术距离开始的。 交错矩阵几何在二次型理论和典型群中有很重要的作用。 1966年，刘木兰[1]用极大集的方法证明了任意域上交错矩阵几何基本定理，后来李迎春[2]将其推广到可交换的主理想整环上,这是一个进步。 对于某一类特殊的交错矩阵，定理条件可不可以更弱一些而结果更简洁一些呢？本文研究了空间中一类特殊矩阵的算术距离的映射的具体形式。

设D是一个除环，F是一个域，D上m×n矩阵的集合记作Mm×n(D)，当m×n时，简记为Mm(D)，Fm×n表示上所有矩阵的集合，In表示Fm×n的n阶单位矩阵，GLn(F)表示F上n阶一般线性群，即所有的n阶可逆矩阵按通常的矩阵乘法构成的群，tA及rank(A)分别表示A的转置和秩。如果F上的n×n矩阵A满足tA=-A且A的主对角线上的元素全为0，则称A为交错矩阵。 域F上所有N×n交错矩阵的集合记作Kn(F)。所有形如(0A-tA0)的矩阵的集合，记作KS2n(F)，其中A∈Fn×n。

1 一些定义和定理

定义 1 ：设A,B∈Mm×n，定义A与B的算术距离为d(A,B)=rand(A-B)，记作d(A,B)。显 然，d(A,B)≥0,d(A,B)=0⟺A=B，d(A,B)=d(B,A)，d(A,B)≤d(A,C)+d(C,B)。

定义 2：域F上的n×n矩阵A,B称为相合的如果存P∈GLn(F)在使得tPAP=B，记作A≈B。

定义3： 设A,B∈Mm×n(D)且rank(A-B)=1，则称A与B粘切，记作A～B。若A,B∈Kn(F)且rand(A-B)=2，则称A与B在Kn(f)中粘切。

定义 4： 设φ是Mm×n(D)到自身的映射，对∀X，Y∈Mm×n(D)如果X～Y推出φ(X)～φ(Y)，则称φ为保粘切的映射。

定义 5：如果对所有A,B,C∈Kn(F)，d(A,B)=d(A,C)+d(C,B)推出

d(φ(A),φ(B))=d(φ(A),φ(C))+d(φ(C),φ(B))，则称映射φ保距离可加性。

引理 1[5]：设A∈Kn(F)(n≥2)，则A的秩必定为偶数，并且如果rank(A)=2r，则

A≈diag(J(r),0)≈((0Ir-Ir0)0)

其中J=(01-10)，J(r)=diag(J,…J)∈K2r(F)

引理 2[4]：设F是域，n是≥4的整数。 如果φ:Kn(F)|Kn(F)是保距离可加性的双射，则φ是保粘切的双射。

证明：设X,Y∈Kn(F)且A～B。 定义映射ψ:Kn(F)|Kn(F)为ψ(X)=φ(X+B)-φ(B)，则ψ也为保距离可加性的双射且ψ(0)=0。由引理1可知，存在P∈GLn(F)使得A-B=tpdiag(J,0)P。设T=A-B+tpdiag(0,Jn-1p)(如果n=2n+1)或者A-B+tpdiag(0,Jn-1)P(如果n=2m)，则其中tP(E2i-1,2i-E2i,2i-1,J(n-1))P。因此从而有

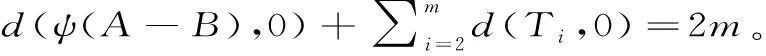
引理 3[3]：设△是除环，m,n是≥2的整数，φ是Mm×n(D)到自身的保粘切的双射，则

1)当m≠n时，φ形如

φ(X)=PXσQ+T,∀X∈Mm×n(D)

(1)

其中P∈GLm(D),Q∈GLn(D),T∈Mm×n(D),σ是D的自同构。

2)当n=n时，除了形如(1)外，φ还形如

φ(X)=tPXτQ+T，∀X∈Mm×n(D)

(2)

其中τ是D的反自同构，P,QT和(1)的意义相同。

引理 4[6]：设D是除环，m,n是≥2的整数，φ是dm×n到自身的保粘切的双射，则φ-1也保粘切。

2 主要结果

下面给出本文的主要结果：一类特殊的交错矩阵几何。易知KS2n(F)是交错矩阵的集合。

定理 1：设F是域，n是≥2的整数，φ是KS2n(F)到自身的保距离可加性的双射，则必有以下形式

φ(X)=tEXσE+G，∀X∈KS2n(F)

其中E(tP00Q)，G=(0T-tT0)，P,Q∈GLn(F),T∈Fn×n,σ是F的自同构。

证明：由引理2可得，φ是保粘切的双射，不妨设φ(0A-tA0)=(0A*-tA*0)， 令φ′:A|A*,∀A∈Fn×n， 易知φ′是双射。

设C=(0A-tA0)=(0B-tB*0),且C～D，其中A,B∈Fn×n， 所以有rand(C-D)=2。

即rank(0A-B-t(A-B) 0)=2,因为rand(A-B)=rank(-t(A-B))，所以rank(A-B)=1。 因为φ是保粘切的双射， 所以有rank(φ(C)-φ(D))=2，即rank(0A*-B*-t(A*-B*) 0)=2，从而有rank(A*-B*)=1，所以由rank(A-B)=1推出rank(φ′(A)-φ′(B))=1。综上可知，φ′是保粘切的双射。由引理4，φ′-1也保粘切。由引理3可知φ′(A)=PAσQ+T，∀A∈Fn×n，其中P,Q∈GLn(F),T∈Dn×n,σ是F的自同构。从而有

φ(0A-tA0)=(0PAσQ+T-t(PAσQ+T) 0)

易知有下式成立

φ(0A-tA0)=(0PAσQ+T-t(PAσQ+T) 0)=t(tP00Q)(0Aσ-t(Aσ)0)(tP00Q)+(0T-tT0)

令E=(tP00Q)，G=(0T-tT0)，则定理得证。

[参考文献]

[1] 刘木兰.交错矩阵几何[J].数学学报, 1966,16 (1) :104-135.

[2] 李迎春.交换的主理想整环上交错矩阵几何[D].长沙:长沙理工大学硕士学位论文，2008.

[3] L. P. Huang,Geometry of Matrices over Ring[M].Science Press,2006.

[4] L. P. Huang, Diameter preserving surjection on alternate matrices[J]. Acta Mathematica Sinica, English Series 2009,25(9):1517-1528.

[5] Z. X. Wan.Geometry of Matrices[M].In Memory of Professor L. K. Hua(1910-1985), world scientific, Singa-pore,1996.

[6] W. L.Huang and Z. X.Wan.Adjacency preserving mappings of rectangular matrices[J]. Beitrage zur Algebr und Geometrie, 2004,45(2) :435-446.