盾构掘进速度对开挖面水头分布的影响
高 健,张义同
(天津大学机械工程学院,天津 300072)
工程监测数据显示,当隧道在低渗透性土壤中以较高的速度开挖时,盾构掘进对隧道开挖面水头分布影响明显,导致作用在隧道开挖面上的渗透力发生显著变化.考虑盾构掘进速度的隧道开挖面水头场分析更符合工程实际.
Marsily[1]提出低渗透性土壤和高储水系数土体中,地下水渗流达到稳态平衡需要更多的时间;Goodman等[2]求解考虑盾构掘进速度的地下水渗流偏微分方程,使用 Du Puit′s 水平流假设对隧道衬砌周围水头场分布进行了分析;Schweiger等[3]提出了考虑盾构掘进速度的三维渗流稳态地下水流动方程;Pottler等[4]将Schweiger的分析方法进入到三维水平瞬态地下水渗流分析中,数值分析取得理想的结果;Anagnostou[5]研究了盾构掘进速度对开挖面附近压力水头变化的影响,提出了修正的考虑盾构掘进速度的三维渗流有限元方程,但文中并没提及渗透力对开挖面稳定性的影响.
本文基于固定在隧道开挖面上参照坐标系,推导了考虑盾构掘进速度、土体的渗透系数以及土体贮水系数的稳态地下水流动偏微分方程.通过伽辽金有限元法推导了考虑盾构掘进速度的二维稳态渗流有限元方程,编制数值分析程序计算稳态地下水流条件下,地下水参数和盾构掘进速度的变化对隧道开挖面附近水头场改变的影响.
1 数值建模
1.1 假定条件及边界条件
为推导考虑盾构掘进速度 v、土体的渗透系数 k以及土体贮水系数s的稳态地下水流动偏微分方程,给出二维渗流的假定条件,即不可压缩流体的假设和水流连续条件,如图1所示.在体积不变条件下,对于饱和土流入微单元的水量必须等于流出的水量,即

即

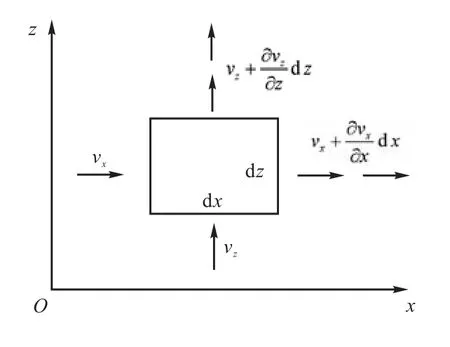
图1 二维渗流连续条件Fig.1 Continuity of two-dimension seepage
基于固定在隧道开挖面上参照坐标系,Anagnostou[5]重新推导了考虑v、k和s的稳态地下水流动偏微分方程.图 2给出新坐标系统下有限元分析的初始边界条件.隧道开挖面被模拟为渗透面,开挖面上总水头 h = x2*,x2*为新坐标系统下开挖面上节点相对原点的竖向坐标.隧道衬砌被视为不可渗透边界.远端边界 BCDA上总水头 h=H,H 指地下水水位到隧道顶部的距离,d为隧道直径.
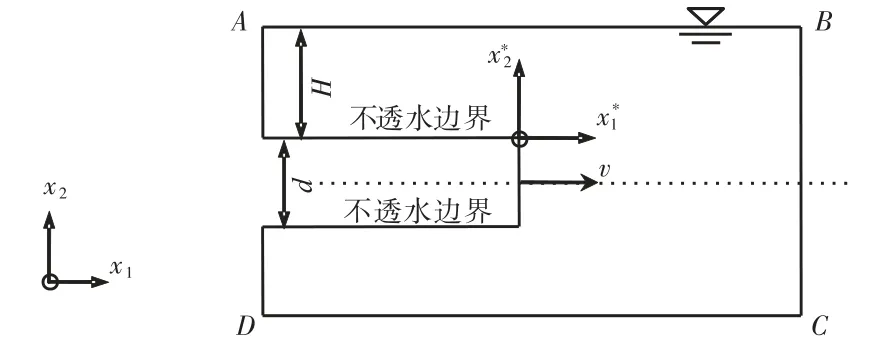
图2 几何模型Fig.2 Geometric model
1.2 数值模型
固定在隧道开挖面上参照坐标系中任一点的位置向量 xk*为


以及

式中:kmδ为Kronecker′s delta;kv为盾构掘进速度向量;xm=(x1x2)T.设定 A (x ,t)为固定坐标系下的压力水头,A*(x*,t)为参照坐标系下的压力水头,两者关系为

考虑式(4)和式(5),对方程(6)进行微分得

式中vm为固定坐标系中的速度向量.
基于固定在隧道开挖面上参照坐标系,隧道进行连续开挖,总水头场的分布将达到稳态,定义为

式(8)变为

固定坐标系下的地下水流动偏微分方程为

由式(3)~式(10),得到基于参照坐标系修正的地下水流动偏微分方程为
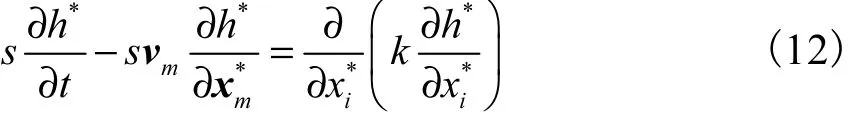
考虑稳态条件下流体流动,式(12)变为

式中 x1*平行于隧道开挖轴线.
进行伽辽金有限元离散,式(13)化为

式中:K为传导矩阵;v为整体开挖速度矩阵;kxv和kzv分别为沿x和z轴的隧道开挖速度.稳态条件下地下水流动方程中与时间相关项消失,则式(14)简化为

1.3 求解方法
编写Fortran有限单元数值计算程序 TME求解考虑盾构掘进速度的三维稳态饱和地下水流动方程.速度矩阵 v为非对称矩阵,必须按全带宽形式存储,尽管传导矩阵 K为对称矩阵,但为了和速度矩阵v相容,仍然按全带宽存储.使用非对称求解程序求解,实现对非对称矩阵的高斯因式分解和回代.
2 水头分布与参数分析
Lee等[6]模拟了盾构开挖过程中地下水渗流的隧道开挖面的渗透力变化情况.砂土地层为摩尔-库仑材料,离心速度为 50,g,将原有小比例模型尺寸放大50倍,取隧道直径 d=5,m,隧道埋深和地下水位为 4倍隧道直径(H/d=4),如图 3所示.值得注意的是,考虑渗流分析时,衬砌管片接缝处是渗漏水的主要部分.本文分析重点放在开挖面附近,对衬砌结构做相对简化,视衬砌结构为连续体,并施加不透水边界条件.在模拟如浅埋隧道的分步开挖与支护中,地下水渗流对衬砌结构的影响不可忽视,需对衬砌结构的接缝认真模拟.
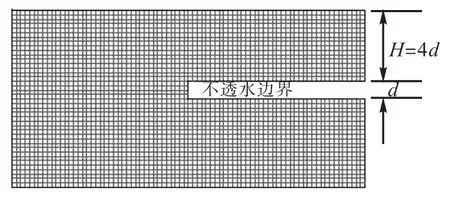
图3 渗流分析有限元模型Fig.3 Finite element model of seepage analysis
本文选取不同地下水条件下的48种工况,研究盾构掘进速度的变化对隧道开挖面附近孔隙水压力场和水头场的影响.表1给出计算条件和工况.

表1 渗流分析工况Tab.1 Cases for seepage analysis
图 4给出工况 1~4的总水头分布等值线.图中数字标出总水头值为 10,m时的等值线.从图中可以看出,随着盾构掘进速度的增加,隧道开挖面附近总水头等值线分布更紧密,水头下降趋势更加明显,水头坡降显著增大.图中同时画出由于支护不当引起开挖面失稳后的滑动体,S1为土体破坏滑动面,S2为隧道开挖面.
图5给出工况4、20和36的总水头分布等值线,研究不同渗透性土壤中隧道开挖面水头场分布情况.从图中可以看出,当盾构以较高的速度v=20,m/d开挖时,低渗透性土壤中隧道开挖面附近总水头等值线分布更紧密,水头下降趋势更加明显.
图6给出工况3、7和11的总水头分布等值线,研究土体贮水系数的变化对隧道开挖面水头场分布的影响.从图中可以看出,总水头值对土壤贮水系数的变化更加敏感,当盾构以 v=15,m/d开挖时,贮水系数增加导致开挖面附近水头坡降显著增大.
综合图4~图6,盾构掘进速度、土体渗透系数和贮水系数是分析开挖面附近水头分布不可忽视的重要因素.在低渗透性及高贮水系数土层中进行隧道开挖,盾构掘进速度的改变将导致开挖面附近孔隙水压力重新分布,进而引起作用在开挖面上渗透力的显著变化.
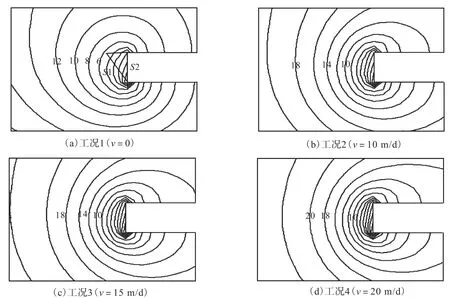
图4 考虑掘进速度的水头分布等值线Fig.4 Hydraulic head distributions according to tunnel advance velocity
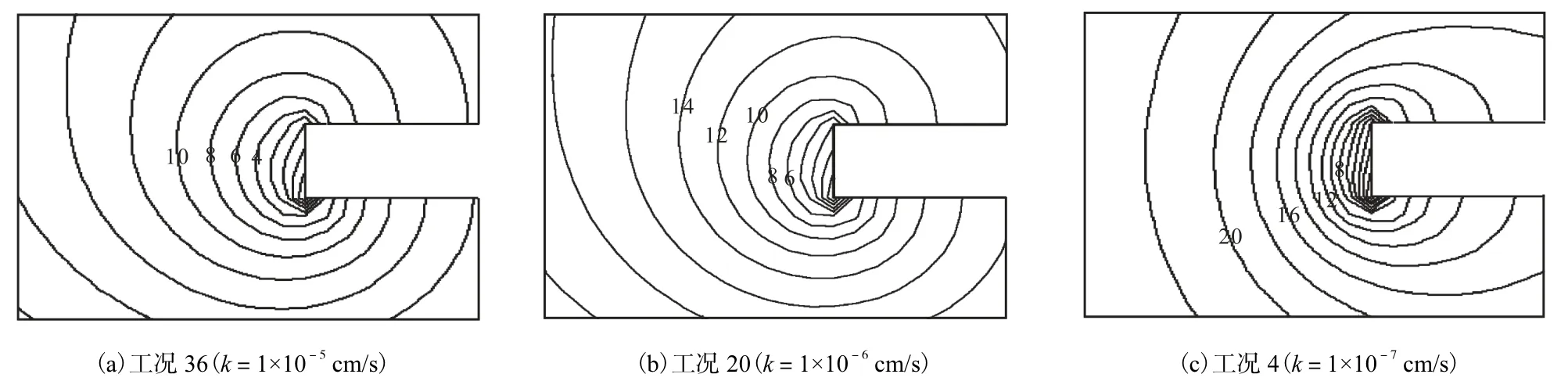
图5 考虑土体渗透性的水头分布等值线Fig.5 Hydraulic head distributions according to ground permeability

图6 考虑贮水系数的水头分布等值线Fig.6 Hydraulic head distributions according to storativity
3 渗透力分析
单位体积土体中,渗透水流对于土颗粒骨架的托拽力fx和fz为

式中wr为水的重度.
对开挖面前方滑动体上单位体积渗透力的体积分应用Gauss理论,得到作用在滑动体上渗透力的水平分量和垂直分量表达式
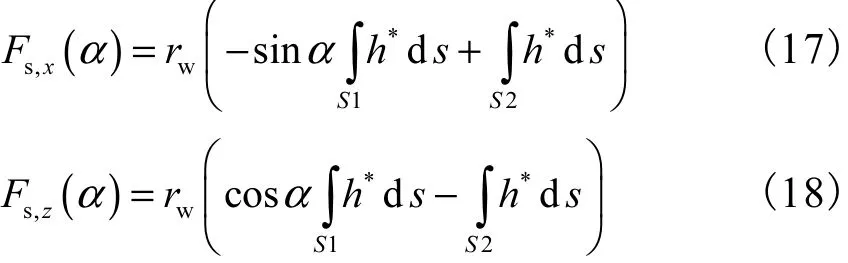
式中:S1为因开挖面失稳引起的土体破坏滑动面,S2为隧道开挖面;α为破坏面 S1与水平面夹角;*h为滑动体内部的平均水头.
Lee在模型中不同位置设置了10个孔隙水压力监测点,用于记录不同埋深和不同地下水水位条件下孔隙水压力变化,实验土体的渗透系数 k取 1×10-5cm/s,.表2给出Lee实验土体材料参数,采用数值计算程序TME计算不同地下水条件下考虑盾构掘进速度的隧道开挖面附近水头分布.由式(16)~式(18),定量分析引起隧道开挖面失稳的水平方向渗透力与静水压力的比值(渗透力比)随盾构掘进速度的变化规律,如图 7所示.图中标识出不考虑盾构掘进速度和贮水系数时,通过实验数据计算得到的渗透力比的结果.nostou推导的楔形体计算模型进一步给出不同地下水条件下维持开挖面稳定的极限支护压力随盾构掘进速度变化的曲线,如图8所示.
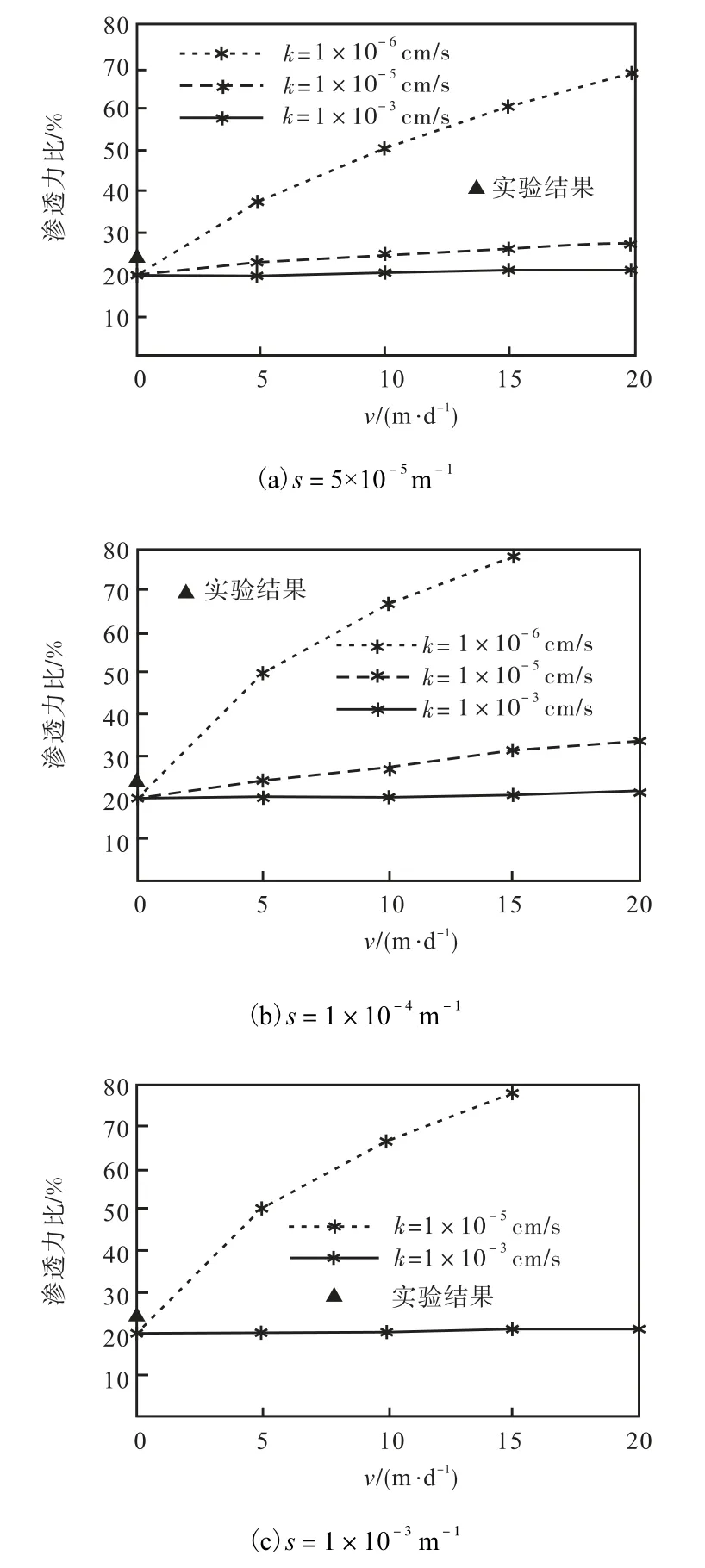
图7 渗透力比与盾构掘进速度的关系Fig.7 Relationship between shield advance velocity and seepage force

表2 土体材料参数Tab.2 Properties of soil material
从图 7中可以看出,当 k取 1×10-5cm/s时,数值计算得到的渗透力比为20%,而实验结果为24%,两者取得较好的一致性.随着盾构掘进速度的增加,渗透力比出现逐步增加的趋势,在低渗透性土层中,这种增加的趋势十分明显.当渗透系数 k=1×10-3,cm/s、贮水系数 s=5×10-5m-1时,盾构掘进速度为20,m/d的渗透力比只相当于掘进速度为 0时渗透力比的1.15倍.当渗透系数k=1×10-6,cm/s、贮水系数s=5×10-5m-1时,盾构掘进速度为 20,m/d时的渗透力比接近掘进速度为0时渗透力比的3.5倍.对比图7(a)、(b)和(c)发现,贮水系数的增加导致渗透力比发生明显的变化,当渗透系数 k=1×10-5,cm/s、盾构掘进速度10,m/d时,贮水系数为s取1×10-3m-1的渗透力比达到s取1×10-4m-1渗透力比的3.2倍.
Buhan等[7]通过数值计算和实验分析得出,盾构在地下水条件下进行隧道开挖,渗透力构成维持开挖面稳定的极限支护压力的主要部分,渗透力的增加是导致开挖面失稳不可忽视的重要因素.Anagnostou等[8]考虑地下水的影响,基于土体稳定的下限解——楔形体法推导出作用在隧道开挖面支护压力的解析表达式.本文考虑表 2的土体材料参数,使用 Anag-
从图 8(a)可以看出,当 s=5×10-5m-1、k=1×10-6,cm/s时,掘进速度为 0,极限支护压力为 45,kN/m2,掘进速度为 20,m/d,极限支护压力达到150,kN/m2,增大近3.3 倍;当 s=5×10-5m-1、k=1×10-5,cm/s时,掘进速度为 0,极限支护压力为 43 kN/m2,掘进速度为 20,m/d,极限支护压力为60,kN/m2,增幅很小.从图 8(b)可以看出,当 s=1×10-3m-1、k=1×10-5,cm/s 时,掘进速度为 0,极限支护压力为 43.7,kN/m2,掘进速度为 15,m/d,极限支护压力已达到180,kN/m2,增大近4.2倍.
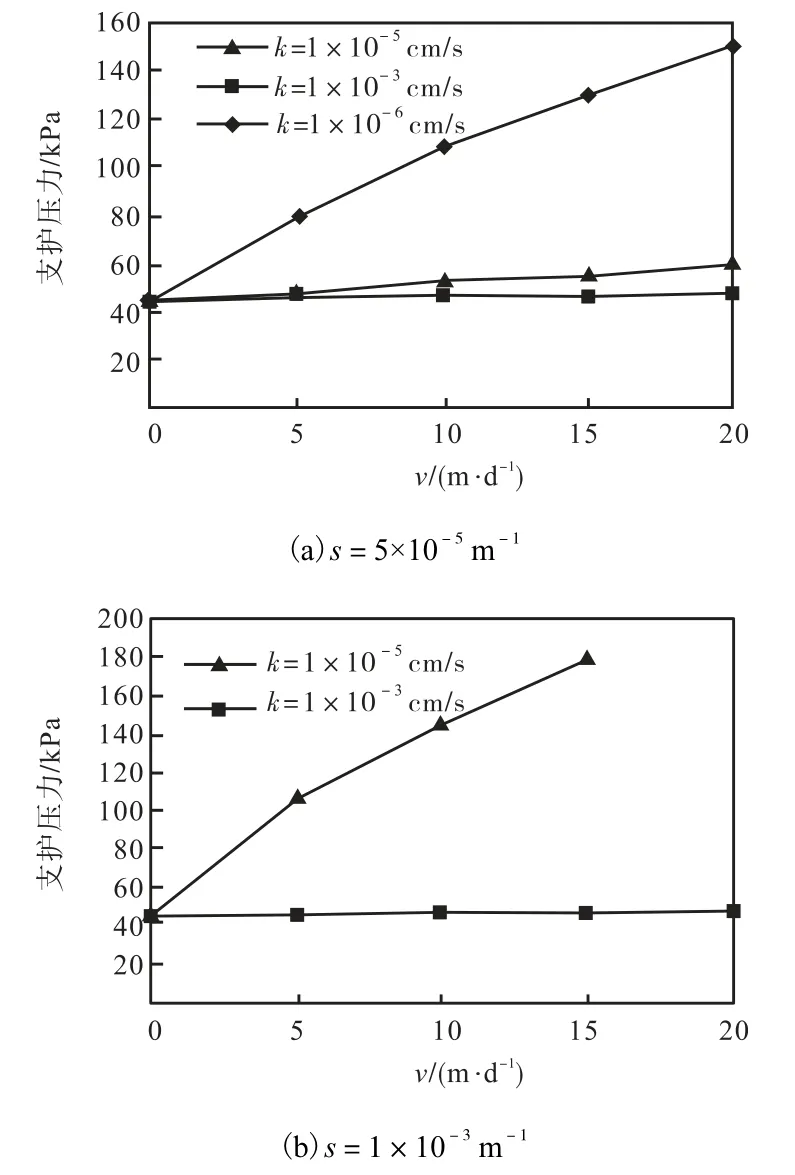
图8 极限支护压力与掘进速度的关系Fig.8 Relationship between tunnel advance velocity and Fig.8 ultimate support pressure
4 结 论
(1) 盾构掘进速度、土体渗透系数和贮水系数对开挖面水头分布产生很大影响.在低渗透性及高贮水系数土层中进行隧道开挖,盾构掘进速度的改变将导致开挖面水头场的重新分布.
(2) 盾构掘进速度的增加改变了隧道开挖面附近水头场的分布,作用在隧道开挖面上的渗透力随盾构掘进速度的增加而明显增大,这种趋势在低渗透系数和高贮水系数土层中显得更为明显.
(3) 盾构掘进速度的增加导致作用在隧道开挖面上渗透力的显著增大,进而引起作用在隧道开挖面极限支护压力的显著改变.因此,改变掘进速度应相应调整极限支护压力以保证开挖面稳定.
[1] Marsily G D. Quantitative hydrogeology [C]// Ground Hydrology for Engineers. London:Academic Press,1986:434.
[2] Goodman R E,Moye D G,Schalkwyk A,et al.Groundwater inflows during tunnel driving [J]. Engineering Geology,1965,2(1):39-65.
[3] Schweiger H F,Pottler R K,Steiner H. Effect of seepage forces on the shotcrete lining of a large undersea cavern [C]// Proceedings of the 7th International Conference on Computer Methods and Advances in Geomechanics. Caims,Australia,1991:1503-1508.
[4] Pottler R,Schweiger H F,Hagemeister A,et al. Influence of tunnel drive on groundwater level [C]// Proceedings of the 8th International Conference on Computer Methods and Advances in Geomechanics. Morgantown,USA,1994:1249-1252.
[5] Anagnostou G. The influence of tunnel excavation of the hydraulic head [J]. International Journal for Mumerical and Analytical Methods in Geomechanics,1995,19(10):725-746.
[6] Lee I M,Nam S W,Ahn J H. Effect of seepage forces on tunnel face stability [J]. Canadian Geotechnical Journal,2003,40(2):342-350.
[7] Buhan P D,Cuvillier A,Dormieux L,et al. Face stability of shallow circular tunnels driven under the water table:A numerical analysis [J]. International Journal for Mumerical and Analytical Methods in Geomechanics,1999,23(1):79-95.
[8] Anagnostou G,Kovari K. Face stability conditions with earth-pressure-balanced shields [J]. Tunnel and Deep Space,1996,11(2):165-173.

