并网型无刷双馈风力发电机组的建模及仿真
李功克 吴 捷 姚国兴
(1.华南理工大学电力学院,广州 510640;2.广东省绿色能源技术重点实验室,广州 510640)
1 引言
当今世界,能源已成为人们生活中最基本的动力。但随着常规能源的日益枯竭,人们正在寻找绿色环保可再生新能源来满足人们日益发展的需要。风力发电作为新能源的典型代表,在各种新能源中具有很大的潜力。作为风力发电系统关键技术的风力发电机,无刷双馈电机的诞生促进了风力发电技术的发展[1]。
风力发电分为离网风力发电和并网风力发电。离网风力发电发电是指区域独立风力发电和分户独立风力发电,一般应用于远离电网的农村边疆地区,作为独立的供电系统。而并网风力发电是将风力发电机发出来的电经过变换器变换成符合电网要求的电能输送回电网。因此,并网型风力发电系统具有较广的发展前景[2]。本文首先介绍了应用于并网风力发电技术中无刷双馈电机的数学模型和仿真模型,在此基础上对并网型无刷双馈风力发电机组进行了仿真模型的建立,最后在 Matlab/Simulink中对并网型无刷双馈风力发电机组分别对启动过程、风速变化、浆距角变化和无刷双馈电机参数变化进行了动态仿真
2 无刷双馈电机的数学模型
无刷双馈电机由于采用比较特殊的定子、转子结构,电机内部的电磁关系比一般的电机要复杂许多,需要针对它的特殊的电磁关系建立新的数学模型。目前无刷双馈电机的数学模型有网络数学模型、同步坐标数学模型、转子速d-q轴模型。
无刷双馈电机的网络数学模型是以定转子的各线圈组的电流作为自变量,线圈组两端的电压作为输入量,用网络分析方法建立起来的一种模型。由于在无刷双馈电机中存在两种不同极对数的定子磁场,在建立数学模型时要采用机械角进行计算。网络数学模型能够较好地反映无刷双馈电机中电流的分布,但模型的建立和计算比较复杂,不利于分解解耦对无刷双馈电机进行控制。
同步坐标数学模型是将功率绕组和控制绕组分别建立在各自的同步坐标下,使各输入输出变量由时变量转换为常量,有利于对无刷双馈电机的控制。但在风力发电系统中,无刷双馈发电机的控制绕组要与变频器相连,变换为双轴模型的控制绕组物理变量不易与变频器接口直接耦合,给仿真实验带来了困难。
转子速d-q轴模型是在同步坐标数学模型的基础上建立起来的,将两相垂直静止坐标系(D,Q)变换成两相同步旋转坐标系(d,q)。无刷双馈电机的d-q轴变换有利于控制绕组变量与变频器衔接和对其进行控制。本文的研究就是在这种数学模型的基础上。
无刷双馈电机中,转子速坐标系与功率绕组同步坐标系、控制绕组同步坐标系的关系如图1所示[3]。
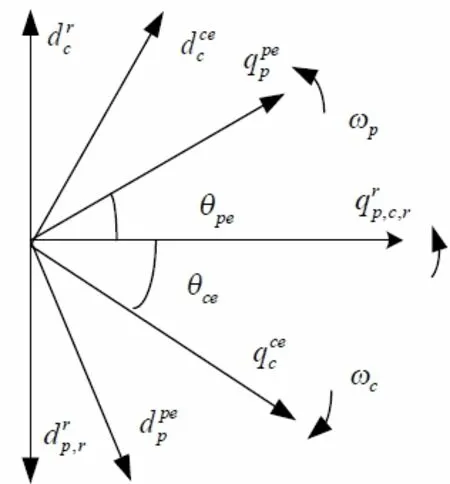
图1 旋转坐标系
图中上标“pe”、“ce”、“r”分别代表功率绕组同步坐标系、控制绕组同步坐标系、转子速坐标系,下标“p”、“c”、“r”分别表示功率绕组,控制绕组和转子绕组,下标“d”,“q”分别表示d轴和q轴。在本文中,取功率绕组极对数pp=3,控制绕组极数pc=1。d-q轴转子速坐标系中无刷双馈电机的电压方程为
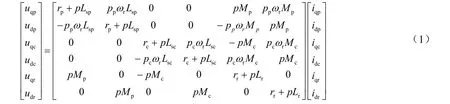
电磁转矩方程为
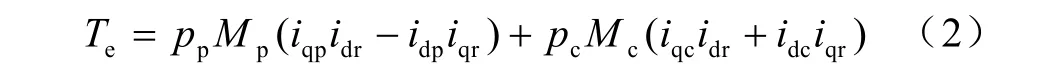
式中,rp,Lsp,rc,Lsc,rr,Lr分别是功率绕组和控制绕组的电阻和自感。Mp,Mc是分别是功率绕组与转子,控制绕组与转子的互感[4]。在M atlab/Simulink中建立的无刷双馈电机仿真模型如图2所示。
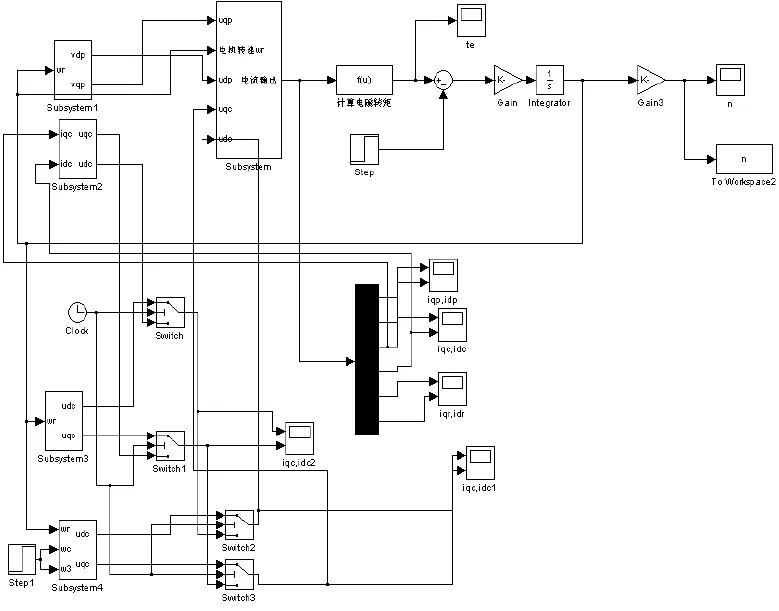
图2 基于M atlab/Sim ulink的BDFM仿真模型
其中Subsystem中的无刷双馈电机数学模型如图3所示。
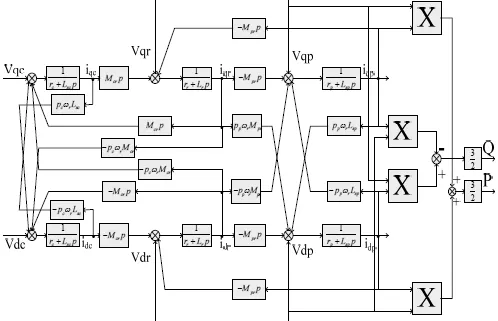
图3 BDFM仿真的数学模型
3 并网型无刷双馈风力发电机组的建模
并网型无刷双馈风力发电机组框图如图 4所示,风能驱动风力机转动,风力机将捕获的风能通过传动机构传递给无刷双馈风力发电机,无刷双馈电机通过矩阵式变换器将发出来的电能反馈回电

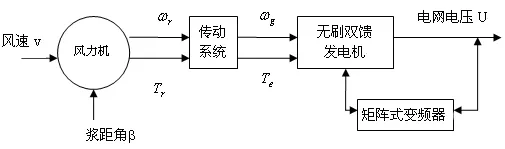
图4 并网型无刷双馈风力发电机组框图
网。其中描述风力机的数学模型为[5]其中,Jr为风力机的转动惯量,ωr为风力机转动角速度,Kr为阻尼系数,Tα为风力机吸收的动力转矩,Tα的大小可表示为
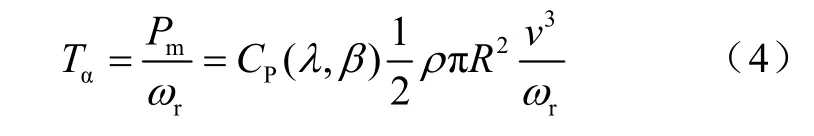
其中,Pm为风力机所吸收的功率, CP(λ,β)为风力机的功率系数,λ为叶尖速比且 λ=ωrR / v,β为叶片的浆距角,ρ为空气密度,R为风力机半径,v为风速。由于 CP(λ,β)与风力机结构相关,本文采用式(5)描述的特性曲线,该曲线具有一定的普遍性。

无刷双馈发电机在风力发电系统中,可根据风力资源状况工作于同步、亚同步、超同步三种状态。在亚同步时,控制绕组需从电网吸收能量;而在超同步时,功率绕组和控制绕组二者都向电网输送电能,要求变频器能够实现能量的双向流动。因此在这里采用矩阵式变换器作为双向功率变换器。
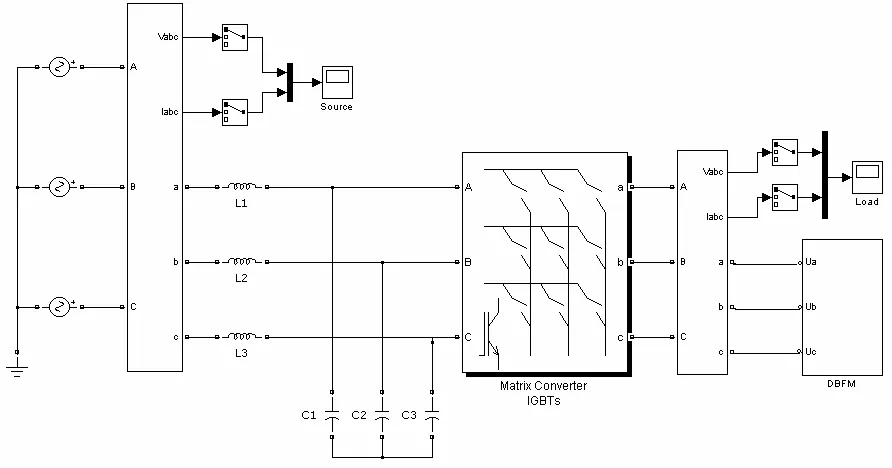
图5 矩阵式变换器仿真模型
仿真模型如图5所示,矩阵模型有3条输入3条输出,在每条输入输出的交点上有1个双向开关,总共有9个双向开关。矩阵变换器是一次变换器,无需储能单元,通过控制开关管的开通与关断,即改变输入项与输出项的连接方式,实现变频输出[6]。
4 并网型无刷双馈风力发电机组的仿真及仿真结果分析
风力系统无刷双馈发电机在双馈运行时具有同步特性,当外界扰动使电机与同步转速有偏差时电机会产生一个整步转矩将电机重新牵入同步运行状态。无刷双馈电机的转速是由功率绕组和控制绕组的电源频率共同决定[7]。功率绕组与电网直接连接,其电压源为50Hz,380V。由式(7)得控制绕组的电压源为10Hz,350V。
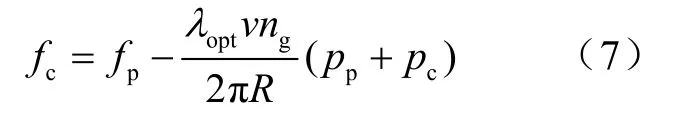
其中,λopt为最优叶尖速比,ng为发电机转速,。下面对无刷双馈风力发电机组不同条件下的动态响应进行了仿真实验风速为8m/s时,风力发电机组在零初始状态下启动时的动态特性如图6所示。
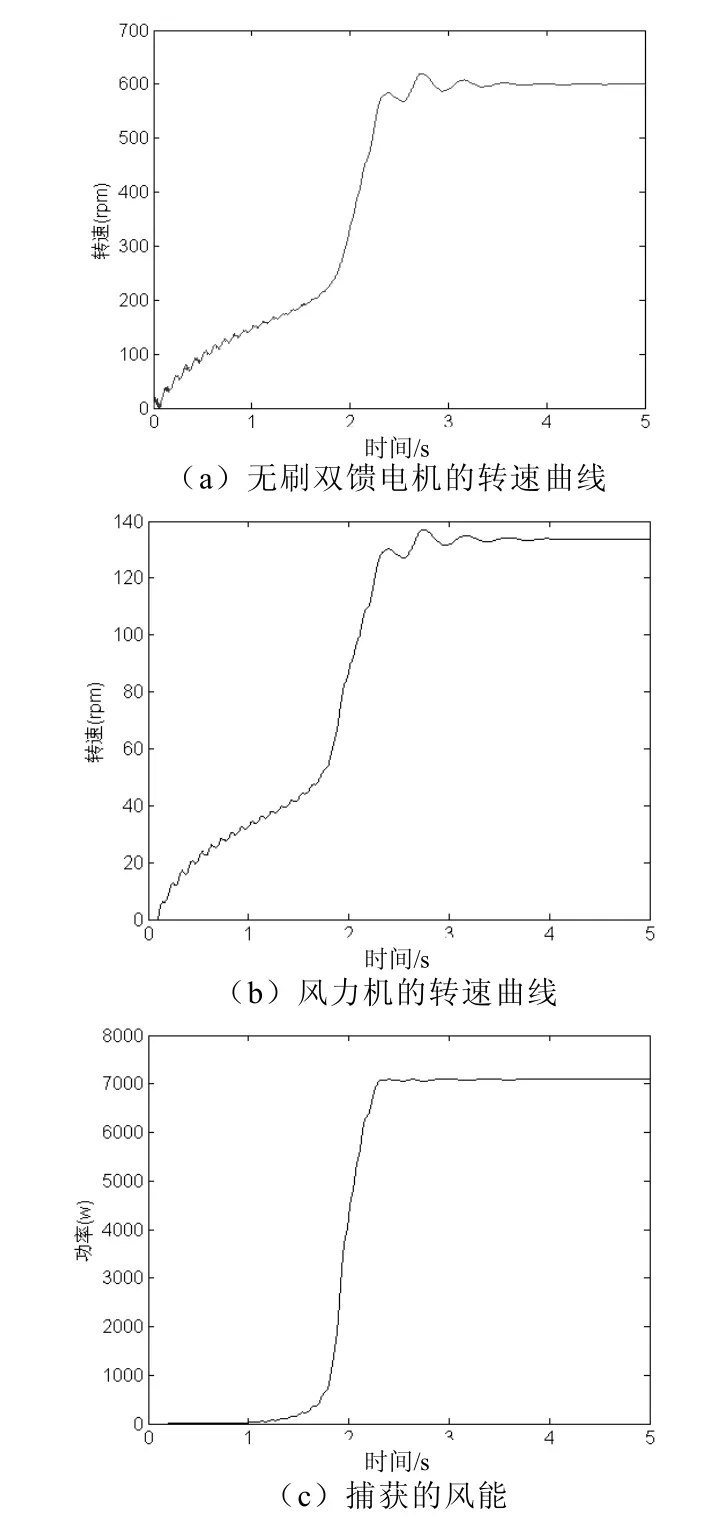
图6 风力发电机组零初始状态下启动的动态特性
图6(a)为无刷双馈发电机的转速从0上升到600rpm,符合稳态运行时转速表达式图6(b)为风力机速度从0上升到134r/m in;图6(c)为捕获的风能。
由于风力发电机组是非线性系统,为能更直观表现运行条件变化时无刷双馈电机的运行特性,采用相对误差的表达形式来进行仿真。在风力发电机稳态运行的基础上,风速降低1m/s,即风速从8m/s降低到7m/s时,风力发电机组各变量相对误差的动态响应如图7所示。
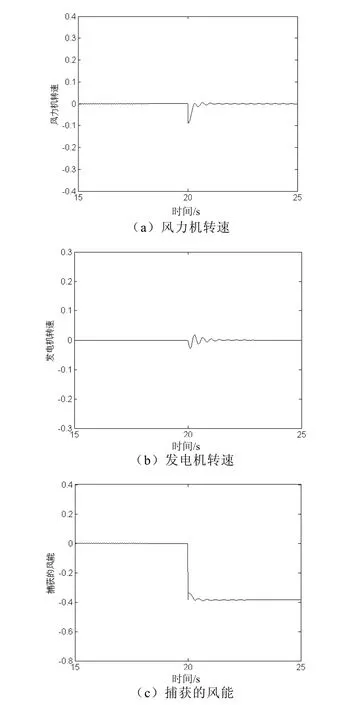
图7 风速降低1m/s时风力发电机组的动态响应曲线
在风速不变稳态运行的基础上,桨矩角变化2弧度, 即桨矩角从0弧度增加到2弧度时,风力发电机组各变量相对误差的动态响应如图8所示。
在风力发电稳态运行的基础上,当控制绕组电压降低5V, 即控制绕组电压从350V降低到345V时,风力发电机组的动态响应见图9。
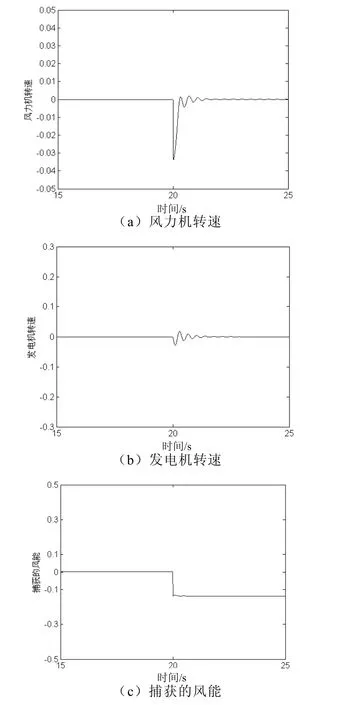
图8 桨矩角变化2弧度时的风力发电机组的动态响应曲线

图9 控制绕组电压降低5V时的风力发电机组的动态响应曲线
从以上仿真图形中可以得到,经过动态过程后,风力发电机转速与发电机稳态转速均保持为改变前的值,这是因为无刷双馈风力发电机工作在双馈方式下,能够保持同步特性;当风速降低、浆距角增加时,由于输入能量下降,捕获的风能均减少;当控制绕组电压降低时,达到稳态后捕获的风能没有变化,这是在两个稳态之间的过渡过程。
5 结论
通过对并网型无刷双馈发电机组各个部分的数学分析,建立了并网型无刷双馈发电机的仿真模型,同时在Matlab/Simulink进行了动态仿真。仿真结果说明了该仿真模型的正确性,同时也说明了并网型无刷双馈发电机优越的运行特性,为以后有关风力发电的并网运行奠定了良好的基础。
[1]王承煦,张源.风力发电[M].北京:中国电力出版社,2003.
[2]叶杭冶. 风力发电机组的控制技术[M].北京:机械工业出版社,2006.
[3]张先勇,吴捷,杨俊华,杨金明. 无刷双馈风力发电机滑模功率解耦控制[J].太阳能学,2007,28(1):68-73.
[4]孙国霞,李啸骢,蔡义明. 大型变速恒频风电系统的建模与仿真[J].电力自动化设备,2007,27(10):69-73.
[5]张琦玮,蔡旭.最大风能捕获风力发电系统及其仿真[J].电机与控制应用,2007,34(5).
[6]黄科元,贺益康,卞松江.矩阵式变换器交流励磁的变速恒频风力发电系统的研究[J].中国电机工程学报,2002, 22(11):100-105.
[7]黄守道.无刷双馈电机控制方法的研究[D].武汉: 湖南大学, 2005.

