基于组织点充满度的机织物图像自动倾斜纠正
陶 晨(浙江农业商贸职业学院,浙江 绍兴 312000)
基于组织点充满度的机织物图像自动倾斜纠正
陶 晨
(浙江农业商贸职业学院,浙江 绍兴 312000)
倾斜纠正一直是织物图像自动分析和处理的瓶颈所在,故提出一种织物图像自动倾斜纠正的方法。首先,使用数学形态学操作对织物图像进行预处理,达到去噪和增强的目的;然后采用大津法和光栅扫描定位图像中的目标矩形,从而决定织物组织点的轮廓。在此基础上提出了组织点充满度的概念,并探讨了组织点充满度与织物图像规正角之间的联系,从而进一步提出了规正系数的概念,用以克服织物扭曲对组织点充满度分析的干扰,准确、全面地确定织物图像的规正角。
织物图像;倾斜纠正;组织点充满度;规正角;规正系数;图像分析
近年来,随着计算机图像处理技术的发展,织物图像分析和识别业已成为纺织数字化技术中的研究热点之一。庄国瑜等[1]运用小波多频道分解方法提取图像的水平分量和竖直分量,得到织物图像的经纬向信息。李艳梅等[2]运用功率谱分析和自相关分析,确定经纬纱密度和组织循环纱线数。高卫东等[3-4]根据纱线的实际排列特点,对经纬纱线密度用不同的方法予以识别。
目前为止,各种相关研究方法与技术都建立在严格规正的织物图像之上。对于倾斜的图像,需要事先在预处理环节中进行人工纠正,才能为后道的分析和识别技术利用。然而,实际操作中获取的织物图像难免有一定的倾斜度,人工倾斜纠正因而成为织物图像自动化分析与识别过程的瓶颈所在。本研究提出一种基于组织点充满度分析的方法,实现织物图像的自动倾斜纠正。
1 图像预处理
本研究使用数学形态学[5]来进行图像的预处理。图1a是一幅用摄像头获取的放大10倍的3枚斜纹织物(经密542根/10cm,纬密390根/10cm)的图像,该图像相对于垂直方向倾斜26°。经过256阶灰度化处理后,首先对图像运用形态学开运算,以达到去除噪音和平滑图像的目的,如图1b所示。接着,对图像运用形态学增强,以提高目标与背景之间的对比度,如图1c所示。
2 组织点轮廓测定
在织物图像中,组织点是具有相对一致的形状特征和亮度范围的图像区域,这为测定各个组织点的轮廓提供了可能性。本研究把图像中满足一定灰度范围的矩形区域称为目标区域。利用OTSU方法[6]做图像分割,可计算得目标区域的灰度阈值范围。然后,基于光栅的图像扫描可找出每个目标区域的位置。图2a中虚线所包围的区域是一组灰度在235以上的目标区域。

图1 图像的预处理Fig.1 Image Pretreatment
确定了目标区域的位置之后,从区域中心向四周发出用于测定边界的射线,射线在灰度衰减积累到一定程度时终止,如图2b。连接所有射线的终止点就构成了组织点的轮廓线,如图2c。

图2 组织点轮廓测定Fig.2 Determination of Interlacing Point Outlines
3 组织点充满度分析
织物图像逆时针旋转一定的角度后,其经向(或纬向)与图像边缘平行,把这个角度称为织物图像的规正角,此时的织物图像称为规正图像。找出规正角后,即可对织物图像实施准确的倾斜纠正。
设织物图像中某一组织点轮廓所包围的像素面积为A,将其逆时针旋转角度θ(0°≤θ≤90°),所得外接矩形的面积为Sθ,令fθ=A/Sθ×100 %。fθ称为该组织点在角度θ上的充满度。图3所示为一个组织点在不同角度上的充满度。

图3 组织点充满度Fig.3 Interlacing Points Fullness
对照图1a不难看出,使得组织点充满度最大的角度即是接近织物图像规正角的角度。然而,实际拍摄的织物图像不只存在倾斜现象,还存在扭曲现象,仅从个别组织点来判断图像的规正角难以取得全面、准确的结果。
设织物图像中存在n个组织点轮廓,在角度θ上各个组织点充满度之和为Fθ,方差为σθ,令Cθ=Fθ/(1+σθ)。Cθ称为织物图像在角度θ上的规正系数。σθ越小,说明Fθ越可靠,综合考虑了两者,规正系数在一定程度上克服织物图像中的扭曲现象给规正角分析带来的干扰。
本研究利用C#编程实现了织物图像自动倾斜纠正算法,图4为程序绘制的图1a所示织物图像在0°~90°各个角度上的规正系数,或称规正系数数组。
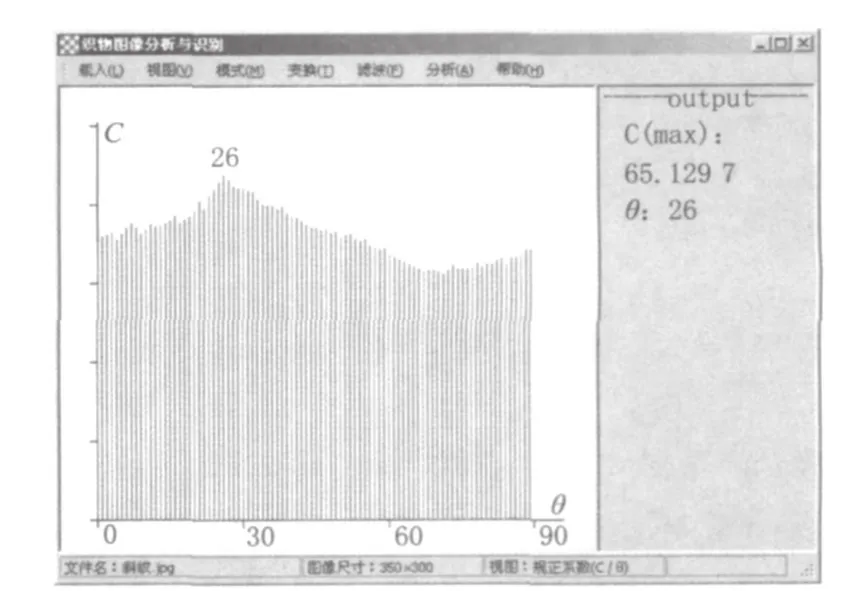
图4 斜纹织物的规正系数数组Fig.4 Correcting Coeffi cient Array of Twill Weave
从图4看出,θ=26°时规正系数最大,据此推断:该角度是织物图像的规正角,将原图逆时针旋转26°可得到规正图像。这与在图1a中观察到的事实相符。
本研究还发现,与斜纹织物相比,平纹和缎纹织物表面由于没有明显的纹路效应的干扰,因而其图像规正角上的规正系数更为显著。图5、6分别为平纹(密度560×520 根/10cm)和五枚缎纹(密度476× 55 根/10cm)及其规正系数数组。

图5 平纹织物及其规正系数数组Fig.5 Correcting Coeffi cient Array of Plain Weave
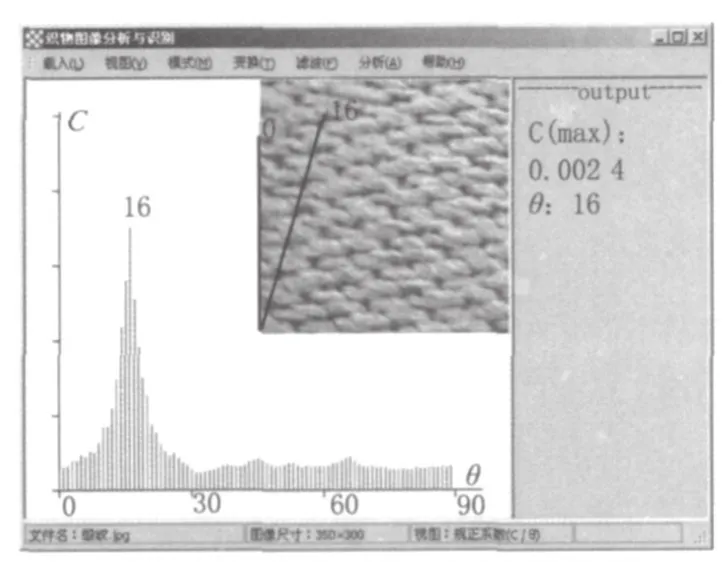
图6 缎纹织物及其规正系数数组Fig.6 Correcting Coeffi cient Array of Satin and Sateen Weave
4 结 语
实验表明,在组织点充满分析的基础上,利用规正系数可以有效地自动纠正织物图像倾斜角度。其算法简单、可靠,非常适合编程实现。该方法能为织物图像自动化分析与识别这一课题的研究提供有益的工具和手段。
[1]庄国瑜,孙悦.织物纹理计算机图像处理的多频道分解方法[J]. 天津工业大学学报,2001,20(3):26-28.
[2]李艳梅,徐伯俊,高卫东.织物组织结构参数自动识别系统的研究[J].北京纺织,2002,23(2):54-57.
[3]高卫东,刘基宏,徐伯俊,等.织物中纬纱排列参数的自动识别[J].棉纺织技术,2002,30(1):28-31.
[4]高卫东,刘基宏,徐伯俊,等.织物中经纱排列参数的自动识别[J]. 棉纺织技术,2002,30(3):31-34.
[5]唐常青.数学形态学方法及其应用[M].北京:科学出版社,1990,445-454.
[6]付忠良.图像阈值选取方法[J].计算机应用,2000,20(5):37-39.
Automatic Weave Image Tilt Correction based on Interlacing Point Fullness
TAO Chen
(Zhejiang Agriculture & Trade Occupational Academy, Shaoxing 31200, China)
As tilt correction has always been the bottleneck of automatic weave image analysis and processing, this paper proposed a means by which automatic weave image tilt correction can be achieved. First, mathematical morphology is carried out in weave image preprocessing for de-noise and enhancement. OTSU and raster scanning are followed to detect target rectangles in the image so as to determine the outlines of interlacing spots, on which the Interlacing Spot Fullness (ISF) is established. Then the relationship between ISF and the correcting angle of weave image is discussed and the correcting coefficient built on ISF is used to counteract the disturbance of weave surface distortions in order to identify the correcting angle in a comprehensive way.
Weave image; Tilt correction; Interlacing point fullness; Correcting angle; Correcting coefficient; Image analysis
TS103.4;TP911.73
A
1001-7003(2010)07-0010-02
2010-04-27
陶晨(1981- ),助教,主要从事纺织新产品开发及纺织数字化检测技术的研究。

