三角高程测量方法研究

罗彩霞，朱少刚

（四川大学锦城学院土木与建筑系，四川成都 611731）

三角高程测量方法研究

罗彩霞，朱少刚

（四川大学锦城学院土木与建筑系，四川成都 611731）

本文结合传统测量方法的不足，提出了全站仪高程测量的新方法.该方法的优点是在观测的过程中不需要量测仪器和棱镜高，从而达到提高精度的目的，在一定条件下该方法可以代替三、四等水准测量.此方法用在施工测量中可以大大地提高工作效率和缩短工程工期.

角高程测量 全站仪 误差分析

在工程的施工过程中，常常涉及到高程测量.传统的测量方法是水准测量、三角高程测量.两种方法虽然各有特色，但都存在着不足.随着全站仪的广泛使用，使用跟踪杆配合全站仪测量高程的方法越来越普及，使用传统的三角高程测量方法已经显示出了他的局限性.经过长期摸索，总结出一种新的方法进行三角高程测量.这种方法结合两种传统方法的优点，使三角高程测量精度进一步提高，施测速度更快.

本文系统地阐述了三角高程测量的传统方法以及新方法的原理，比较其优劣性，并且对三角高程测量过程中的主要误差及测量精度进行了分析.

1 三角高程测量的传统方法与新方法原理

传统三角高程测量的基本公式为：

其中，HA为已知点高程，HB为待求点高程，D为两点间的水平距离，а为在A点观测B点时的垂直角，i为测站点的仪器高，t为棱镜高.传统方法中，全站仪必须架设在已知高程点上，同时要测出待测点的高程，必须量取仪器高和棱镜高.

如果我们能将全站仪像水准仪一样任意置点，而不是将它置在已知高程点上，同时又在不量取仪器高和棱镜高的情况下，利用三角高程测量原理测出待测点的高程，那么施测的速度将更快.如图1，假设A点的高程已知，B点的高程为未知，这里要通过全站仪测定其它待测点的高程.

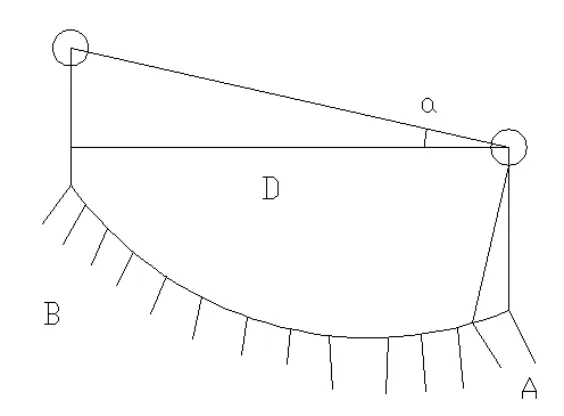
图1 三角高程测量示意图

首先由三角高程测量原理可知：

式中i，t都是未知的.但有一点可以确定即仪器一旦置好，i值也将随之不变，同时选取跟踪杆作为反射棱镜，假定t值也固定不变.从（2）式可知：

由（3）式可知，基于上面的假设，HB－i＋t 的值在任一测站上也是固定不变的，而且由于HA和Dtanа均为已知，所以可以计算出W值.

这一新方法的操作过程如下：

如图2所示，A点为已知高程，B点为未知高程，将仪器架设在AB两点的中间C点，C点和已知高程点A通视.用仪器照准A点，测出V1值，即V1＝D1tanа1，并算出W的值，W＝HA＋D1tanа1.此时与仪器高程测定有关的常数如测站点高程，仪器高，棱镜高均为任意值，施测前不必设定.然后将C点高程设定为W，仪器高和棱镜高设为0即可，这时以C点为已知高程点，照准待测点B测出其高程，即

故使用该方法测得B点的高程为

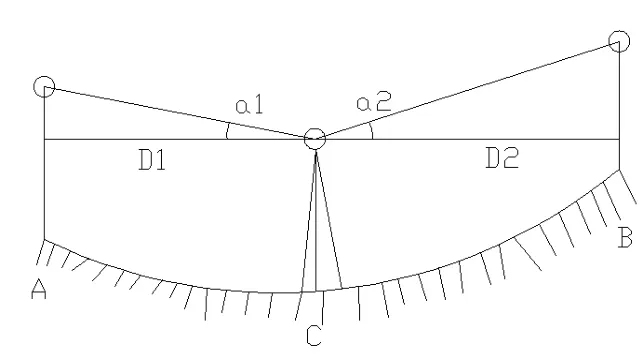
图2 新三角高程测量方法示意图

综上所述，将全站仪任一置点，同时不量取仪器高，棱镜高，仍然可以测出待测点的高程，测出的结果从理论上分析比传统的三角高程测量精度更高，因为它减少了误差来源.同时需要指出的是，在实际测量中，棱镜高还可以根据实际情况改变，只要记录下相对于初值t增大或减小的数值，就可在测量的基础上计算出待测点的实际高程.

2 三角高程测量的精度控制

采用新的方法进行三角高程测量不用量取仪器高和棱镜高，简化了测量步骤，同时减少了误差来源，提高了观测精度.

2.1 精度分析

由以上可知，已知高程点A和未知高程点B之间的高差为

下面对其精度进行分析，为便于微分，将式（6）变为

S1和S2分别为已知高程点A和未知高程点B上的棱镜到仪器的斜距，如图3所示

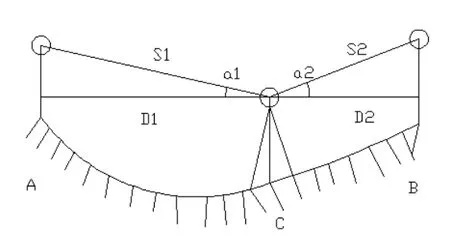
图3 新三角高程测量精度分析原理图

对式（7）进行全微分，得

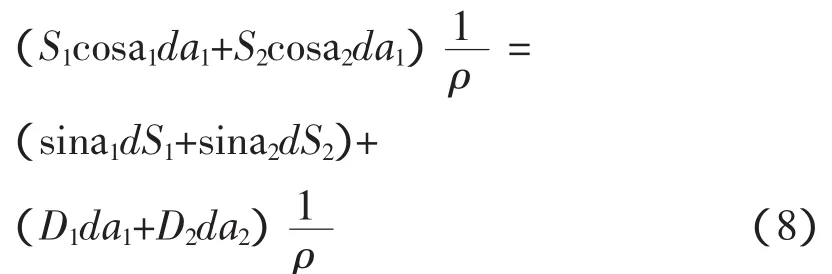
式中第1项为测距误差引起的高差误差，第2项为测竖角误差引起的高差误差，其中，D1、D2为前、后视平距.根据误差传播定律，将式（8）变换为高差中误差计算公式为

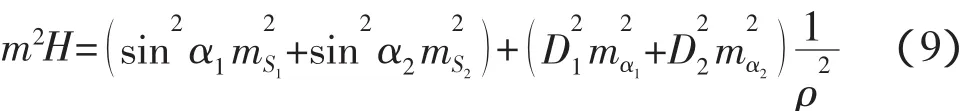
由于在施测过程中前、后视距接近相等，如果再要求前、后竖角也尽量接近相等，则可假设D1≈则式（9）可简写为

若往返测量，则一测站高差中数的中误差为

按水准测量高差全中误差计算公式

则每千米高差全中误差为

其中L为前后视距之和.

2.2 精度估算

下面以工程中经常采用的全站仪（标称精度：测角为±2″，测距为±（2 mm±2 ppm×D）为例，按视距长短和竖角大小分别对测角、测距引起的误差及高差中误差精度估算见表1、表2、表3.

从上面的分析和表中的计算可以看出，高差测量的误差与竖角的测角引起的误差近似成线性的关系，影响显著，而测距误差的影响很小，故在高差测量中应尽量高竖角的测角精度，同时对竖角角度和视距进行限制，这样更能提高高差测量的精度.若以表3.3中中误差的2倍作为高差测量的限差，当竖角在25°以内，前、后视距不超过700 m与规范中三等几何水准测量允许的每千米高差全中误差和水准线路闭合差限差进行比较有，

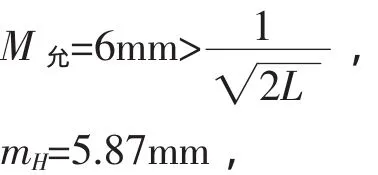
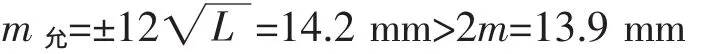
能满足三等水准测量的要求.所以当竖角在25°以内，前、后视距不超过700 m，此三角高程新方法可以代替三、四等几何水准测量，特别在丘陵和山区，在满足精度的情况下，能提高工作效率，缩短工程工期.

表1 测角引起的误差

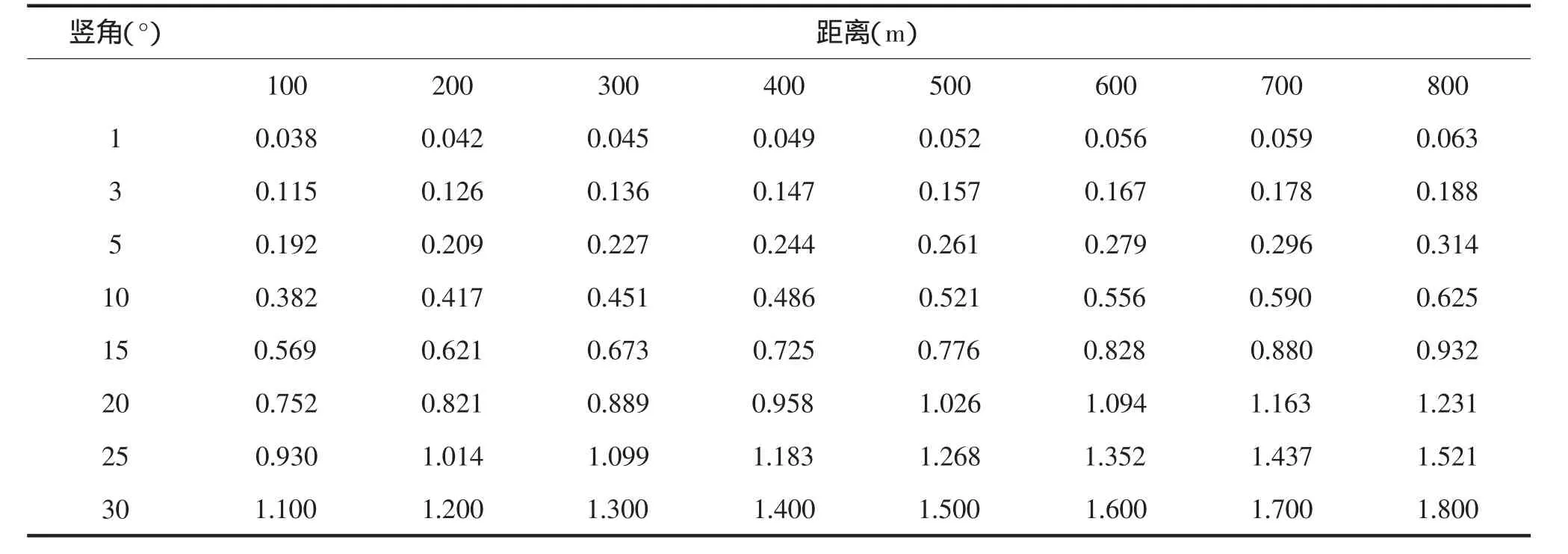
表2 测距引起的误差

表3 高差中误差m的估值

3 结论

通过分析三角高差测量新方法及其误差，得出一下结论：

1）使用全站仪进行水准测量或三角高程测量，可以在任意点安置仪器，减少测站数，又不必丈量仪器高和棱镜高，就能测出高差或高程，施测速度较快.

2）观测过程中不需要量测仪器和棱镜的高度，减少了误差来源，提高了精度.

3）观测过程中全站仪居中安置，尽量让前、后视相等，从而可以有效地减弱或消除地球曲率和大气折光对高差测量的影响，又进一步提高了精度.

4）该方法既有几何水准测量任意置站的特点，又同时不受观测地形的限制，特别适合在丘陵、山区测绘.在一定条件下可以代替三、四等几何水准测量，提高了外业作业效率.

5）若用工程中常采用的全站仪（标称精度：测角为±2″，测距为±（2±2 ppm×10－6×D）mm，在一定条件下，按照仪器的操作规范进行操作很容易使高差测量精度达到三、四等几何水准测量精度的要求.

[1]张正禄.工程测量学[M].武汉:武汉大学出版社.2002.

[2]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社.2003.

[3]工程测量规范GB 50026-2007.中国人民共和国国家标准[S].北京:中国计划出版社.2008.

Abstract：In this article，we propose a new total station measuring method from combining the defect of traditional measurement methods.The advantages of this method is it can improve the precision without measuring height of device and prism，and it can replace the third and fourth level of measurement under certain conditions.This method can greatly improve efficiency and shorten the project duration in the construction survey.

Key words：trigonometric leveling；total station；error analysis

〔编辑 石白云〕

Research on the Trigonometry Elevation Measurement

LUO Cai－xia，ZHU Shao－gang
（Department of Civil and Architecture Jincheng Academy，Sichuan University，Chengdu Sichuan，611731）

P204

A

1674－0874（2010）05－072－03

2010-06-03

重庆市科委自然科学基金计划资助项目［CSTC，2008BB9317］

罗彩霞（1982－），女，甘肃康乐人，双学士，测绘助理工程师，研究方向：土地规划管理.