星敏感器标定方法的研究现状与发展趋势
孙高飞,张国玉,郑茹,杨孟飞,郝云彩
(1.长春理工大学,长春 130022;2.北京控制工程研究所,北京 100190)
星敏感器在航天飞行器的姿态测量和控制系统中起着重要的作用,是最精密的姿态测量部件。它的发展主要经历了星跟踪器、第一代 CCD星敏感器、第二代 CCD星敏感器三个主要阶段。目前,随着航天技术的发展,对航天飞行器姿态测量精度提出了更高的要求,从而促进了姿态敏感器的迅猛发展。星敏感器是通过其光学系统测量天球上不同位置的恒星,得到观测星图,并与由星表数据库产生的导航星图进行特征匹配,来实现对空间飞行器的三轴姿态的测量[1]。所谓三轴姿态测量是利用卫星上的姿态敏感器测量所得到的信息,经过适当的处理,求得固连于卫星本体的坐标系相对空间某参考坐标系中的姿态。姿态确定的输入信息是姿态敏感器的测量数据,输出是卫星的三轴姿态参数[2]。
星敏感器的精度标定是实现其姿态准确测量必不可缺少的重要环节。星敏感器的标定是指对其不同的物理参数(如:光学镜头的焦距,中心点偏移,CCD噪声等)进行估计。为了达到测量精度的角秒级,对星敏感器的标定与校准就应该力求对尽量多的物理参数进行评估。
星敏感器的标定分为在轨标定和地面标定。随着星敏感器在空中的使用,其发射时受到的冲击、工作环境的改变以及长期工作带来的老化和磨损,都会使其内部参数发生变化。为了保证星敏感器的测量精度和可靠性,有必要对其进行在轨标定。现有的在轨标定方法有两类,一类是依据外部姿态信息的校准,另一类是根据星内角距原理的校准。前一类方法要求事先提供一个已知的精确姿态,且如果提供的姿态存在误差,则该误差会引入校准过程中。并且,由于星敏感器已经是各类航天飞行器上精度最高的姿态测量部件,要为其提供更高精度的姿态参考信息是比较困难的。后一类方法是基于星间角距不变的原理,检测在轨飞行期间星内角距测量值和真实值之间的偏差,利用优化算法估计出标定参数。
1 星敏感器在轨标定研究现状与发展趋势
1.1 国外研究现状
在轨标定是高精度卫星姿态确定与控制系统的重要组成部分。星敏感器作为卫星姿态测量的高精度仪器,目前可以提供最高精度的姿态信息。为了保证给出高精度姿态信息,应对其进行标定工作。星敏感器的标定分为地面标定和在轨标定。通常地面标定是通过建立星敏感器测量模拟对相关参数进行标定,主要有安装矩阵、焦距、主点位置等,但由于地面标定受到环境和模拟条件的影响,难以模拟卫星飞行器在轨器件的真实环境,并且,随着工作环境的变换以及发射时受到的冲力等,都将使星敏感器的各项参数变化,所以为星敏感器提供一种在轨标定方法是十分必要的。国外学者对在轨标定方法很早就进行了深入的研究。
1981年,Shuster.M.D.和Oh.S.D.两位学者关于姿态敏感器相对准线安装误差进行了研究,被誉为在轨误差估计的先驱。该算法突破了以往仅仅依靠飞行器发射前的数据统计结果,进行姿态敏感器准线安装误差标定的限制。但是,该算法忽略了校正和冗余,而且建立的模型粗糙,使得对姿态敏感器在轨标定中的误差较大。虽然算法有很多不足之处,但作为对姿态敏感器准线安装误差在轨标定的首次尝试,并且由于其具有有效性和鲁棒性,在之后NASAGoddard Space FlightCenter的几乎每一次任务中都得到了有效应用[3]。
1988年,Davenport.P.和Welter.G.提出了Davenport算法,用于估计陀螺的准线安装误差和标定因子误差。算法要求对姿态的估计和对陀螺的标定分开独立进行,而且陀螺的各种误差不是自相关,即相互独立的。该算法是次优的,只考虑了陀螺的准线安装误差,而并没有考虑其它姿态敏感器的准线安装误差[4]。
1989年,Bar-Itzhack.I.Y.提出了一种用于姿态敏感器准线安装误差估计的Kalman滤波算法,该算法使用四元数作为系统状态向量,使协方差矩阵产生了奇异性,而且在其建立的系统模型中多个状态量都是不可观测的。
1990年至1994年,Shuster.M.D.,Pitone D.S.和 Shuster.M.D.,Shuster M.D.和 Phone.D.S.等在多篇文献中详细叙述了姿态敏感器相对和绝对准线安装误差的在轨标定。除对陀螺以外的姿态敏感器的相对准线安装误差参数进行了直接估计,该算法相对简单,但是要求各种敏感器的采样时间必须同步,陀螺的输出用于调整非同步的采样。且详细叙述了敏感器绝对准线安装误差的概念和用法,说明了三自由度的姿态参数是不可观测的,除非由负载直接给出姿态数据[5]。
Shuster M.D.用 Friedland的偏差估计理论和Gupta和Mehra最大似然估计理论,提出了一种采用六状态Kalman滤波估计姿态和准线安装误差参数的递推最小二乘估计器。Friedland的偏差估计理论通过各种假设将姿态误差估计从动力学状态估计中解出来,即初始状态估计误差和初始状态偏差估计误差的叉乘为零,而且假设状态偏差不由过程噪声驱动。理论上,姿态估计滤波器由姿态测量信息进行初始化,系统的安装误差是由系统温度变化和过程噪声引起的,然而Friedland的偏差估计理论的假设条件中忽略了这两个理论。而且,在实际应用中并没有发现这样的假设带来的局限性,同时也说明了该假设条件是合适的,并且说明了这样假设可以减少该算法的计算量,增加计算的鲁棒性[6]。
2001年,Pittelkau.M.E.采用UD分解处理系统过程噪声协方差矩阵,提出一种对姿态敏感器安装误差进行在轨标定的Kalman滤波算法(AKF)。在该算法中,作者考虑了两个星敏感器的绝对准线安装误差,一个惯性敏感器组件(由三个光纤陀螺组成)的绝对准线安装误差。算法中系统模型是非线性的,但其线性化的误差很小,因此该算法是最优的。该算法对地面标定仍然有效。
1.2 国内研究现状
国内在对于星敏感器在轨标定方面的研究落后于国外,但是近些年来,其发展速度极快,进而使星敏感器的精度得到了不断的提高。其中2005年由北京控制工程研究所提出的方法中,将惯性敏感器与星敏感器的在轨自主标定进行了比较,最终总结出惯性敏感器对于星敏感器标定的使用准则。哈尔滨工业大学卫星技术研究所提出了一种适用于星敏感器和陀螺联合在轨标定的算法,通过陀螺给出星敏感器外部姿态的对星敏感器进行标定。同时,星敏感器又可以标定陀螺随时间积累的误差,由此提高卫星姿态确定精度[7]。
2007年哈尔滨工业大学卫星技术研究所又提出天基载荷对星敏感器在轨标定算法,该方法利用天基载荷对无穷远恒星成像,提出了最小二乘算法,卡尔曼滤波算法结合最小二乘估计值来得到卡尔曼滤波量测量,设计了一种新滤波算法对星敏感器进行在轨标定,最后进行了仿真计算并对算法进行了比较分析,仿真结果表明新滤波算法对星敏感器系统常值误差标定结果比较理想。
2008年哈尔滨工业大学卫星技术研究所提出三种星敏感器的在轨标定方法。一种是星敏感器自主在轨标定算法,有最小二乘最优估计法在轨标定星敏感器星像点偏移和光学透镜焦距变化,以最小二乘最优估值为量测,Kalman滤波算法设计了星敏感器在轨自主标定模型[8-10]。其仿真实验结果表明:利用该在轨标定算法可以对星敏感器的主点位置变化和光学系统的焦距变化给出精确的标定结果。另一种方式是通过高精度陀螺对星敏感器进行标定的算法研究,利用高精度陀螺为星敏感器提供连续的三轴姿态信息,再通过积分运算就可以得到姿态角信息,再由卫星姿态运动学方程,利用卡尔曼滤波算法,就可以对星敏感器的常值误差和噪声等设计在轨标定模型。利用陀螺的测量输出对其进行实时补偿,以确保姿态测量元件在轨工作精度。仿真结果表明该在轨标定算法可以准确标定出星敏感器的常值误差。星体姿态角估计误差优于0.0005rad。第三种是基于陆标敏感器对星敏感器在轨标定算法。针对星敏感器系统常值误差进行了在轨标定的算法研究。通过陆标模拟器对一些目标点进行图像匹配,与基准图像的对应点进行坐标比较,利用最小二乘法的最优估计值作为量测,然后应用卡尔曼滤波算法得到一个敏感器的在轨标定模型,经过仿真计算后发现,这种在轨标定算法可以标定出星敏感器的系统常值误差[11-13]。
同年北京科技大学提出了一种基于 RAC约束(Radial Alignment Constraint)的星敏感器在轨校准方法。该方法不依赖外部姿态信息,通过建立基于RAC约束的星敏感器成像模型,采用两步法从单帧星图解算出外部参数和内部参数,并利用多帧星图整体优化的方式得到内部参数的整体最优解。仿真实验表明,该方法能有效消除内部参数与外部参数耦合,实现其准确分离和解算。在星点位置噪声方差为0.05 pixel的情况下,该方法能准确解算出内外参数,其残差在x方向为0.063pixel,在y方向上为 0.053 pixel。
2010年由北京控制工程研究所和中国空间技术研究院提出一种基于现有在轨方法,在重点分析了星敏感器焦距和主点等内部参数的在轨标定方法后,采用扩展卡尔曼滤波对在轨星图进行处理。仿真结果表明,焦距和主点估计值的扩展卡尔曼方法较最小二乘估计法,其收敛速度快、稳定性好且精度高,在5000幅星图后输出即可稳定,可有效去除星点随机误差影响,提高标定精度。本方法介绍的在轨标定方法只使用于内部参数标定,尚不可用于待定系数标定[14,15]。
同年由北京航空航天大学提出一种基于卡尔曼滤波的星敏感器在轨校准方法。根据星敏感器光学镜头以径向畸变为主的特点,采用一阶径向畸变模型,利用摄像机标定中的径向排列约束(RAC),对其外部姿态和内参数进行在轨校准。以采集到的星点的图像坐标和对应导航星在天球坐标系下的赤经、赤纬信息作为滤波器的输入,外部姿态和内参数作为输出,构造相应的状态方程和观测方程,进行两次卡尔曼滤波迭代,结果作为校准参数的最优估计。仿真实验表明:本方法能消除内部参数与外部参数的耦合,校准过程不依赖外部姿态,且状态方程和观测方程均为线性方程,满足卡尔曼滤波迭代的最优条件,能够精确估计出星敏感器内外参数,在星点成像位置噪声标准差为0.05像素时,校准后x、y方向上的平均误差分别为0.044像素和0.049像素[16-18]。
2 星敏感器地面标定方法和标定设备的现状和发展趋势
2.1 地面标定方法的现状和发展趋势
由于航天技术的特殊性,对星敏感器的标定多采用地面测试、星图模拟的方法来进行,主要标定安装误差、光学系统存在的误差因素(如 CCD平面的倾斜角和旋转角、镜头畸变、焦距测量误差)、加工装配误差、电子线路误差等,这种标定方法称为地面标定方法。地面标定根据实施方法的不同,又分为非设备式标定方法和采用地面标定设备方法(地面标定的设备多为星模拟器)。按照工作方式的不同,一般又把星模拟器分为两类,标定型星模拟器和功能检测型星模拟器。标定型星模拟器的实质是一个平行光管,在焦面位置放置星点板,经光源照射后,星点板就可以通过平行光管成像到无穷远来模拟星图,在光源前放置不同的中性滤光片实现对不同星等的模拟,放置带通滤光片实现对恒星光谱的模拟。这种星模拟器的结构简单,没有实时性要求,但对单星张角、星点位置和星等的模拟精度要求很高。功能检测型星模拟器的主要功能则是可以在地面上进行星图模拟,产生的实时星图要和待测星敏感器的工作状态相匹配,以便对星敏感器的星点提取和星图识别算法进行功能测试。这种星模拟器结构较为复杂,对星图刷新率和模拟星图的星间角距精度要求极高。但是,作为星模拟器显示核心器件的光阀,国内研制水平很低,国外对我国的出口限制,因此制约了星模拟器的发展。
2.2 国外地面标定设备的研究现状
国外主要做标定型单星模拟器,且在这方面的技术相对比较成熟。但对功能检测型星模拟器的研究较少。
原民德蔡司厂研制的用于星敏感器静态测试的静态星模拟器,基于分划板作为星模拟器的分划板,在不透光的分划板上刻有可透光的微孔。光源经准直光学系统点亮星点分划板上,就可以完成模拟天空中恒星的目的。其中准直光学系统由四个准直光管组成,属于多光管式星模拟器,其在星点板上可有16个微孔可以模拟出16个星点,通过星点板位置可通过微调机构进行调整以保证其位于准直光管的焦面上[19]。
美国伊斯曼-柯达公司研制的用于星敏感器静态测试的星模拟器,以光纤板作为星点板,模拟等腰三角形状的星图,将不同色温的光通过光纤引到准直光学系统的焦面上,并在光路中加入不同的滤光片来模拟-2-8 等星[20]。
天穹星空模拟器,它由一个16英寸的测地圆顶构架组成,构架上有许多对准位于构架中心的53M-2型模拟器的景物投影器,该系统为多星模拟器提供了适合的辐照度和各种状态,并且星投影器方位可根据需要在9.5立体角范围内移动和重新安装。星投影器位置按照实际天空中星体位置安装,误差不超过10角秒。三轴转台运动以模拟飞行器在空中运动,此时敏感器视场出现不同星,从而输出卫星姿态并对其给予校正。它可以在星等、光谱、大小上达到较高精度,且可以对敏感器进行一定功能检测,但体积庞大且受到安装限制,无法按实际天空中星的布局安装,且所安装星投影器数目受限。
美国休斯公司研制了一种星场模拟器,使用了液晶光阀作为星图的核心显示器件,在显示屏上可以通过计算机控制星点亮灭来完成星图的动态显示,在星敏感器的入瞳处产生模拟星图,供星敏感器接收,完成星图捕获、星图识别、星点位置计算等动态模拟效果,最终达到校正卫星姿态的目的。这款星模拟器无论在星图模拟精度还是星图模拟的稳定性方面,都得到提高[21,22]。
美国的Mc Donnel l Douglas Aerospace公司公布的星敏感器地面测试设备可以提供三组互不相关的模拟星图,视场范围是25°×25°,其中使用了具有高分辨率的显示器作为星图显示器件,其分辨率为4096×4096,图像刷新率为1000Hz。且每幅星图可以模拟50颗星,单星张角精度可到100″,模拟星等范围是 2-8 等[23,24]。

图1 EADS公司的星敏感器和星模拟器图Fig.1 EADS company's star sensor and star simulator map
欧洲宇航公司(EADS Astrium)又率先提出了星模拟器显示器件的变革,如图1所示。采用硅基液晶(LCOS)作为显示屏,这样就可以将对比度提高并且细分,其研制的星模拟器视场达到直径25°,星间角距误差在18″以内(2),对准精度优于3.6″,并且重量小于2kg,大大的实现了小型化、高精度化。
2.3 国内地面标定设备的研究现状
国内对星模拟器的研究是从二十世纪七十年代末开始,进入九十年代后,国内相关的研究所和高校才对动态星模进行探索性的研究。
在八十年代主要是单星模拟器的研究,由长春光机所率先研制的单星模拟器具有良好的性能,无论从星点的成像质量,模拟光谱类型还是绝对光度都达到技术要求。中国科学院成都光电所研制的高精度星敏感器标定仪,也是一台性能很好的静态单星模拟系统,在配合高精度二维转台后可以在特定的视场范围内完成动态标定;在“八五”期间,由北京控制工程研究所成功研制了第一代全天球实时恒星模拟器,使用TFT式便携式计算机液晶作为星图显示器件,模拟视场可达6°×6°,在单星位置精度方面,可以做到 30″以内,但其体积大且精度差,在使用操作方面也十分不方便。
九十年代,星敏感器稍有发展,星模拟器的研究才更近一步,1995年中科院光电所与北京502所联合研究的小型动态星模拟器,该星模拟器将液晶光阀作为星图显示器件,经过准直光学系统后模拟星图的视场角可达6.5°×5°,在单星位置精度方面可以做到在30″以内,并且实时全轨道星模拟器的识别精度也小于30″,同时其重量小于5kg,实现了星模拟器的小型化发展;哈尔滨工业大学在1998年研制的多星模拟器,该星模拟器的星图显示器件使用了类似笔记本电脑的液晶屏,分辨率193mm×145mm,对于准直光学系统的设计要求为=1638.77mm,=1/32.77;西南科技大学研制的多星模拟器,星图显示器件采用 T FT-LCD液晶光阀,通过准直光学系统后模拟的视场大小为16.2°×12.1°,星间角距误差小于40″,并且具有轻型化的特点,重量仅为3kg。
进入二十一世纪后,随着航天水平的提高,对星敏感器的精度要求也越来越高,针对高精度星敏感器的标定方法研究也刻不容缓,由此促进了星模拟器的迅猛发展。
北京航空航天大学研制的一款高精度且低成本的星模拟器,利用星图模拟计算机控制高精度星图模拟器算法,实现了星图的静态和动态的高精度模拟。
中国科学院西安光学精密机械研究所研制的模拟17个星等的高精度星模拟器,对星等的模拟精度可达±0.05星等,对单星平行度的模拟精度优于±1″,并且使用闭环控制方式,对光源的稳定性进行自动控制,是系统具有高稳定性。如图2为高精度星模拟器结构示意图。

图2 高精度星模拟器结构示意图Fig.2 Schematic diagram of high-precision star simulator
北京控制工程研究所研制的静态多星模拟器。该系统包括法兰和至少四个均能产生一颗模拟星的星光管,其光谱和亮度都可以单独进行调整。通过角度调整机构将星光管安装在法兰上,并可在大于10°的范围内调整任意两个星光管的相对角度,以此产生构型不同的多副模拟星图。其光源采用三色发光二极管,每个星点的亮度和光谱特性都单独可控,如图3所示。

图3 静态多星模拟器的工作原理图Fig.3 The work of a static multi-satellite simulator schematic
2003年电子科技大学与中科院光电技术研究所研制了小型星模拟器,如图 4 所示为其系统实物图,星图动态显示采用TFT-LCD显示器件为核心元件,对于星等的模拟范围是2~6.5mag(仪器星等),星等模拟精度为±0.3mag,准直光学系统的视场为8°×6°,单星张角优于30″,模拟光谱范围为0.47~0.75m,中心波长为0.59m,从模拟的各项技术指标来看,它可以满足实际检测需要,而且结构简单。

图4 小型星模拟器Fig.4 Small star simulator
长春光学精密机械与物理研究所研制的基于数字光处理(DLP)技术的星模拟器,实现了模拟星等范围为2.0~ 8.0等星,准直光学系统的视场为10.5°×7.5°,且单星张角优于 40″,能为星敏感器提供任一时刻、任一惯性坐标系下指向的模拟星图,可满足星敏感器标定工作中对小型星模拟器的动态性、大视场、宽星等范围、短采样周期等需求。其系统框图如图5所示。
北京航空航天大学与航天时代电子公司合作设计研制了一套天文导航半物理仿真系统,对星图识别算法及星敏感器性能进行了静态试验和动态试验。该天文导航半物理仿真系统中的星模拟器采用了日本精工公司的TFT液晶光阀作为显示器件,对于星等的模拟范围为2~7等星,模拟精度为±0.5等,准直物镜的视场角为10°×8°,出射星光的平行度小于15″,模拟的星间角距精度优于20″。
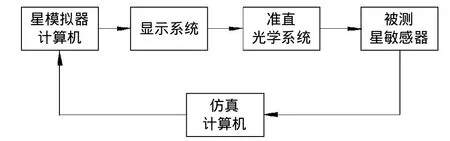
图5 星模拟器系统框图Fig.5 Star simulator system block diagra
长春理工大学利用星点分划板研制了视场为20.2°×20.2°的静态星模拟器,其单星张角≤35″,星对角距误差≤45″,可模拟星等为2~8等星。
哈尔滨工业大学研制一种星模拟装置,如图6所示。对该装置所采用的准直光学系统、数字可调光源进行了研究,并提出了背景光模拟的技术要求。该装置能模拟0~5等星,背景光均匀性为94.7%,系统焦距为1647 mm,视场为28′,准直性优于±2″。同时模拟星光和背景光变化,具有准直性好、背景光照度模拟范围宽等优点,能够满足天文导航设备的实验室检测要求。

图6 星模拟装置结构示意图Fig.6 Schematic diagram of star simulator
长春理工大学利用高分辨率 TFT-LCD研制了视场为 20.2°×20.2°的动态星模拟器,其单星张角≤50″,星对角距误差≤50″,可模拟星等为2.0~6.0Mv。。其三维模拟框图如图7所示。
综上所述,现有的国内外地面标定方法,只能满足中高精度星敏感器标定精度的要求,为了完善星敏感器甚高精度标定的理论,填补甚高精度星敏感器标定设备的空白,以满足我国未来航天事业发展的需要,有必要开展深空导航星敏感器甚高精度标定技术的研究。

图7 动态星模拟器三维模拟图Fig.7 Dynamic three-dimensional simulation maps star simulator
3 结束语
本文介绍了星敏感器的发展现状,作为航天飞行器三轴姿态的重要测量工具,星敏感器可提供高精度姿态信息,它从星跟踪器发展到 CCD星敏感器再到APS有源器件星敏感器,可见星敏感器正向着高可靠性、小型一体化、自主、大视场、高数据更新率、高精度的方向发展。对于星敏感器的标定方法做详细介绍和分析总结,发现随着星敏感器自身精度的不断提高,无论是对其地面标定方法还是在轨标定方法,都提出了更高的要求,本文介绍的星敏感器在轨标定方法和地面标定方法,可以为研究甚高精度星敏感器及其标定方法与设备做理论基础。
[1]孙宝祥,李铁寿.三轴稳定通信卫星在地球指向模式下的陀螺标定[J].航天控制,1994,(3):64-68.
[2]赵黎平,周军,周凤岐.基于磁强计的卫星自主定轨[J].航天控制,2001(3):7-11.
[3]Shuster M D,OHS D.Three-axis attitude determination from vector observation[J].Journal of Guidance and Control,AIAA-81-4003,1981,1(4):70-77.
[4]Snow F,Krack K,Sheu Y,et al.Accuracy study of the upper atmosphere research satellite(UARS)definitive attitude determina-tion[J].Flight Mechanics/Estimation Theory Symposium,1988,10(11):26-41.
[5]Shuster Malcolm D,Pitone Dantel S,Bierman Gerald J.Batch estimation of spacecraft sensor alignmentsⅠ.Relative alignment esti-mation[J].The Journal of the Astronautical Sciences,1991,4(39):519-545.
[6]Uneet Singla D,Todd Griffith,J.L.Crassidis andJ.L.Junkins.Attitude Determination and Autonomous On-Orbit Calibration of Star Tracker For GIFTS Mission.AAS/AIAA Space Flight Mechanics Meeting,San Antonio,Texas,27-30 January,2002:4-11.
[7]刘一武,陈义庆.星敏感器测量模型及其在卫星姿态确定系统中的应用[J].宇航报,2003,24(2):162-167.
[8]杨博.一种用星敏感器自主定位方法的精度分析[J].航天控制,2001:12-16.
[9]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西北工业大学出版社,1998:40-41.
[10]刘建业,李荣冰.一种改进的星敏感器/陀螺卫星定姿算法[J].系统工程与电子技术,2006,28(6):896-899.
[11]陈雪芹,耿云海.一种利用星敏感器对陀螺进行在轨标定的算法[J].系统工程与电子技术,2005,27(12):2112-2116.
[12]张延顺,王海.卫星三轴姿态确定系统的光纤陀螺/星敏感器组合技术研究[J].中国惯性技术学报,2003,11(2):1-4.
[13]周世勤.光纤陀螺技术的发展[J].飞航导弹,2000,2(2):42-45.
[14]杨小会.基于天文信息的卫星自主导航[D].西北工业大学硕士学位论文,2006:16-18.
[15]Thomas Rbekk Krogstad.Attitude Control of Satellites in Clusters.Norwegian University of Science and Technology Department of Engineering Cyberntetics[J].Master's thesis,2005:3-10.
[16]许武军,张海洪.用于微卫星星座的空间监视望远镜系统设计[J].光电工程,2005,32(6):1-3.
[17]王涛,冯展军,尤太华,等.基于星敏感器的飞行器姿态确定方法[J].导航与控制,2005,4(1):15-17,81.
[18]陈刚.卫星自主智能控制多传感器信息处理技术研究[D].国防科学技术大学硕士学位论文,2005:1-3.
[19]Mark E Pitielkau.Kalman filter for spacecraft sys-tem alignment calibration[J].Journal of Guidance,Control and Dynamics,2001,24(6):1187-1195.
[20]Malak A.Samaan,Todd Griffith,Puneet Singla,et al.Autonomous On-Orbit Calibration of Star Trackers.PPT.Paper Presented at Space Core Technology Conference Colorado Springs,Co,2001:1-11.
[21]Puneet Singla.A New Attitude Determination Approach Using Split Field of View Star Camera[J].Texas A&M University MASTER OFSCIENCE,2002:58-61.
[22]Paul Sanneman,Teresa Hunt,Kathie Blackman.Design of the EO-1 Pulsed Plasma Thruster Attitude Control Experiment.Charles Zakrzwski.37th AIAA/ASME/SAE/ASEE Joint Propulsion.Conference.8-11 July 2001.Salt Lake City,Utah:3-11.
[23]Travis,H.D.Attitude Determination Using Star Tracker Data withKalman Filters:[Master's thesis].Naval Postgraduate School,Monterey,CA.Dec 2001:2-11.
[24]胡绍林,黄刘生.自旋稳定卫星姿态参数的容错Kalman滤波[J].中国空间科学技术,2003(1):66-70.

