由一种陷门单向函数构造的秘密共享方案

黄科华

泉州儿童发展职业学院 福建 362000

0 前言

秘密分享是密码学的重要方向之一，自从Shamir在1979年提出了秘密共享体制以来，有关秘密共享体制的研究受到了广泛关注。Shamir的基于Lagrange插值法构造的秘密分享方案和后来的许多相关的方案都是一次性的方案，即各参与者的秘密份额只能使用一次，在每次共享过程后，秘密分发者都要重新分配各参与者的秘密份额。

1 陷门单向函数

定理1： Tp在 m odp2的乘法运算下构成一个群 Tp

定理2定义函数

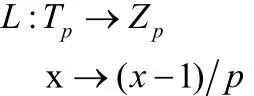
则有对于任意的

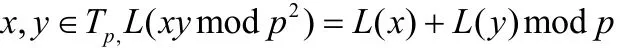
即对于任意的

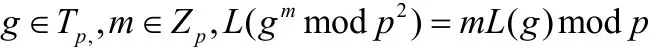
证明：

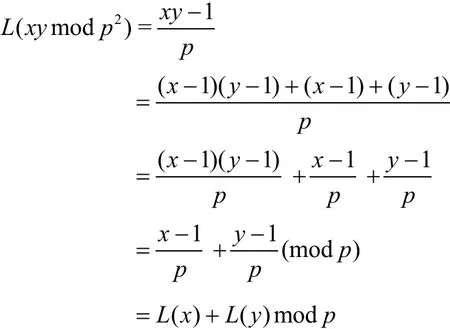
命题得证。

已知y，求(a, β)可以通过以下式子得到：

则

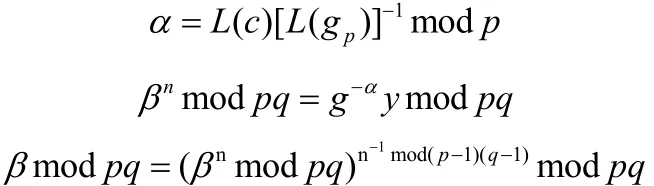
以上为陷门单向函数的构造，由上述可知，设单向函数为G，则由已知α, β求y =G(α, β)很容易，但在不知道n分解的前提下求G1−(y)=(α, β)是不可能的，不过知道了n的分解则为容易，即n的分解为陷门。

2 改进的门限秘密共享方案

该方案是对 Shamir(,)tn门限方案的改进。Shamir的方案是一次性的方案，也就是说当密钥合成之后，下一次如果还需要新的密钥的话，管理者就必须再通过安全信道重新分配一次份额，而在现实中，安全信道是不容易得到的，而且重新分配份额也需要一定的时间。本方案利用了第一部分所提出的函数的单向性构造了一个秘密分享方案，解决了Shamir方案的一次性问题，而且本方案便于成员的加入和删除。

设要分配的密钥为K，以下为方案的内容。

2.1 份额的分配过程

（1）D选择一个大素数，以及n个单项函数Gi(α,β)=,ni=qi,其中ni＜P，i= 1 ,2,… n。D选择n个份额(si;bi)(保密的参数)， si, bi∈GF(P)。D通过安全信道将单向函数与份额分别发给n个用户 Pi,i = 1 ,2,… n 。

（2）D随机选择一个有序对(c,a)(公共的参数)∈GF(P),计算 Gi(csi,a + bi), i = 1 ,2,… n ,并保证当 i≠j, Gi(csi,a+bi)= Gj(c sj,a + bj)。

（3）D通过 n + 1 个有序对(0,K ) ,(i,Gi(csi,a+bi))(i=1,2, · · · ,n)构造 n 次多项式 f (x) 。

（4）D公布(c,a)以及 f (n + i),i = 1,2,… n − t+1。

2.2 密钥的重构过程

t个或者以上用户联合起来就可以恢复多项式 ()fx，从而恢复密钥K：

（1）每个用户 Pi下载(c,a)生成 Gi( c si, a + bi)；

（2）需要合成密钥的 t个用户提供 Gij(c sij,a + bij),j = 1 ,2… t给合成者；

（3）合成者下载 f (n + i ),i = 1 ,2,… n − t +1；

（4）合成者通过掌握的 n + 1 个数值对(ij, Gij(c sij,a + bij))( j = 1,2… ,t ),

(r,f(n + r ) ,(r = 1 ,2… ,n − t +1)来合成密钥：

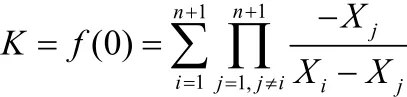
其中用(Xi, Xj)i = 1,2,… n+1来表示所得到的n+1个数值对。

3 对方案的分析

3.1 可行性

n+1个不同的数值对(ij, Gij(c sij,a + bij))( j = 1,2… ,t ),(r,f(n + r )),(r = 1 ,2… ,n − t +1)可恢复n次的多项式 f (x)，而 K = f(0)，可以顺利恢复密钥。

3.2 安全性

（1）由 shamir的(,)tn门限秘密共享方案可知，少于或等于 1t− 个用户联合起来无法恢复多项式 ()fx，得不到密钥的任何信息。

（2）由于iG 的单向性，公布ix=iG(cis,a +ib)与(c,a)并不能求得用户的份额(is,ib)，即便K为系统所恢复也无法得到用户份额的任何信息，因而用户的份额可以重复使用。

3.3 关于系统的更新

（1）当密钥K更新后，管理者只需更新(c,a)(设为(c′,a′)),计算, a ′+bi)，并生成多项式f(x)(设为f′(x))，然后D公布(c′,a′)以及f′(n+i),i = 1,2,…n − t+1，即可按上述方案实行。因而用户手中的份额可以无限次使用，无需管理者再使用安全信道来发送份额。

（2）当有成员加入时，D只需为 pn+1用户随机生成单向函数Gn+1和(sn+1,bn+1)，并通过全信道传输给新用户即可。删除成员时只需更新 f (x)并更新公布 f (n + i ), i = 1,2,… n − t+1。不需要更改用户手中的份额。

（3）某成员份额泄露时，管理者只需要重新发送新份额(s’,b’)，以及更新 f (x) 和更新 f (n + i ),i = 1,2,… n − t+1即可，而无需更换其他成员的份额。

4 结束语

本文在文[2]基础上构了一个单向函数，并结合文[3]SHAMIR的(t,n)门限设计了一个秘密分享方案，在这个方案中，每次合成密钥的时候用户只是提供了部分的份额，攻击者和其他的用户无法通过提供的份额求出用户的份额，所以在该秘密共享方案中用户的份额可以无限次使用，而且方案便于成员的加入和删除，当某成员份额泄露时只需改变他的份额即可，无需修改其他成员的份额。层次的学生学习效率都会大大提高。

[1]ascal aillier.A Tradoor ermutation Equivalent to Factoring[J].LNCS 1560.ublic Key Crytograhy: Second International Worksho on ractice and Theory in ublic Key Crytograhy, KC’99, Kamakura,Jaan, March 1999. roceedings. Sringer-Verlag.1999.

[2]T.Okamoto and S.Uchiyama.A New ublic-Key Crytosystem as secure as Factoring[J].LNCS 1403.Advances in Crytology. roceedings of Eurocryt’98.Sringer-Verlag.1998.

[3]Shamir A. How to share a secret. Comm. ACM 1979.

[4]谭凯军,诸鸿文.基于单向函数的动态秘密分享机制[J].通讯学报.1999.

[5]刘焕平,胡铭曾,方滨兴,杨义先.基于单向函数的动态密钥分存方案[J].软件学报.2002.

[6]He J,Daw son E.M ultistage secret sharing based on one2way function[J]. Electron Lett.1994.

[7]吕继强,许卫东,张鸿燕,王新梅.基于离散对数的环签名方案.第一届信息与网络安全会议论文集[J].2003.

[8]Douglas R.Stinson著,冯登国译.密码学原理与实践[M].电子工业出版社.2003.

[9]R.L.Rivest,A.Shamir and Y.Tauman,How to leak a secret [J].In Asiacryt.2001.