基于多极理论传热模型的垂直U型地埋管传热特性研究

於仲义，陈焰华，胡平放，袁旭东

（1. 武汉市建筑设计院，湖北 武汉 430014；2. 华中科技大学 建筑环境与设备工程系，湖北 武汉 430074）

基于多极理论传热模型的垂直U型地埋管传热特性研究

於仲义1，陈焰华1，胡平放2，袁旭东2

（1. 武汉市建筑设计院，湖北 武汉 430014；2. 华中科技大学 建筑环境与设备工程系，湖北 武汉 430074）

地埋管循环介质出口温度不仅仅反映了地埋管的换热能力，同时极大地影响着热泵主机的运行效率，是地埋管换热过程的一个重要能效特性参数，可通过引入能效系数来反映。文基于地埋管轴向流动多极理论传热模型对不同的回填材料物性、支管间距、地埋管埋设深度、土壤物性、管内循环介质流速条件下地埋管传热过程进行动态模拟和分析，得出了各重要特性参数的变化对U型地埋管传热能效的影响规律，可为土壤源热泵地埋管换热器的设计提供参考。

土壤源热泵；地埋管；能效系数；多极理论；热模型

地埋管换热器传热模型是土壤源热泵应用关键技术，也是国内外有关土壤源热泵研究的重点。但地下土壤传热过程的复杂性使得很难对其建立精确的计算模型，迄今为止国际上还没有普遍公认的唯一方法。现有的传热模型大体上可分为两大类。第一类是以热阻概念为基础的半经验性的解析模型[1-2]，此类模型通常都是以钻井壁为界将土壤热交换器传热区域分为两个区域，钻井内部忽略热容量的作用采用稳态传热模型，钻井外部忽略轴向传热采用线热源模型或柱热源模型。第二类方法是以离散化数值计算为基础的数值求解模型[3-4]，可以考虑比较接近现实的情况，此类方法因土壤热交换器传热问题涉及的空间范围大、几何配置复杂，同时负荷随时间变化，时间跨度长达十年以上，按三维非稳态问题求解实际工程问题将耗费大量的计算机时间，在当前的计算条件下直接求解工程问题几乎是不可能的。

基于多极理论的地埋管换热器轴向流动传热模型是参照第一类方法的思想[5-8]。钻井内部使用偏心距线热源的多极理论传热模型，钻井外部使用柱热源模型，并结合地埋管热阻网络平衡原理建立的传热模型[9-11]。本文将基于该传热模型分析地埋管换热器与周围土壤热量传递过程的能效特性。

1 地埋管传热能效特性参数

1.1 地埋管流体出口温度

对于土壤源热泵系统设计而言，地埋管换热器的传热分析主要是保证在土壤源热泵整个生命周期中埋管中循环介质的出口温度都在设定的范围之内，并满足地埋管换热负荷量。因而，在进口温度一定的条件下，地埋管循环介质出口温度不仅仅反映了埋管的换热能力，同时极大地影响着热泵主机的运行效率，是地埋管换热过程的一个重要能效特性参数。

根据基于多极理论的地埋管传热模型，U型埋管两支管的温度分布Tf1(Z, t)、Tf2(Z, t)可表示为[12]：

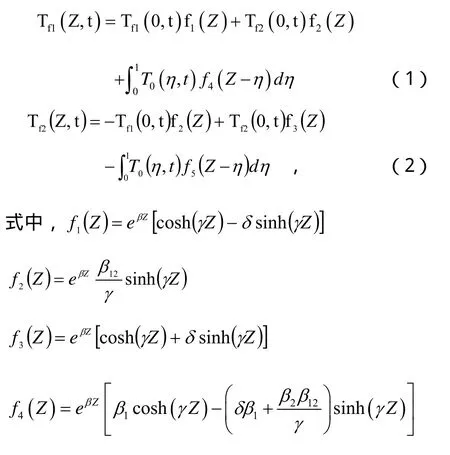
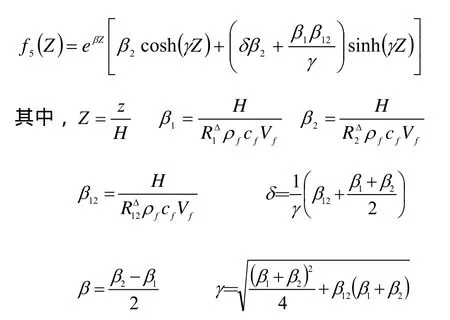
ρf为流体的密度；cf为流体的比热； Vf为地埋管内流体的容积流量；、分别可以看作是支管的流体与土壤无穷远边界之间的综合热阻，为两支管之间的综合热阻。

由定解条件Tfin(t )=Tf1(0,t )，Tf1(1,t)=Tf2(1,t)，则单U型管的流体出口温度为：

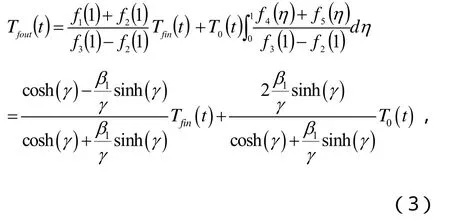
1.2 地埋管传热特性参数——能效系数

与传统的换热器不同的是，地埋管换热器是通过在换热器中流动的循环介质与周围的土壤进行热/冷量交换，土壤的作用相当于一个蓄能体，其逐时蓄能能力要受到地埋管传热的影响发生变化，而不是冷热两种恒定进口参数流动工质之间的热量交换[13]。土壤源热泵机组的出流进入到地埋管换热器的下降支管与周围土壤进行换热，从理论上来说埋管出口温度均可以最大限度的接近土壤初始温度。地埋管换热器在夏季放热状态下，较高温度的冷凝器出口进入到地埋管换热器的下降管，经土壤吸热后温度下降到接近土壤初始温度；地埋管换热器在冬季吸热状态下，较低温度的蒸发器出流进入到地埋管换热器的下降管，经土壤传热后温度能够温升到接近土壤初始温度。从传热温差看，这两种状态地埋管具备较大的换热效果。而实际的状况是，不管是冬季状态还是夏季状态，地埋管换热器的出口温度均远离了土壤初始温度，造成了换热效果下降，其主要原因一方面是经济原因不允许长度较大的地埋管，从而无法使得埋管出口温度无限接近土壤初始温度；另一方面埋管周围土壤经一段时间的排/取热堆积了大量的热/冷量而温度升高/降低，因而换热能力随着时间推移逐渐下降导致出口温度逐渐上升，使得埋管出口温度远离土壤初始温度[14]。

针对地埋管换热器的传热特性，借鉴传统换热器效能的概念，定义U型地埋管换热器能效系数E，为地埋管换热器实际换热量Q与最大理论换热量Q′的比值，其表达式为[15-16]：

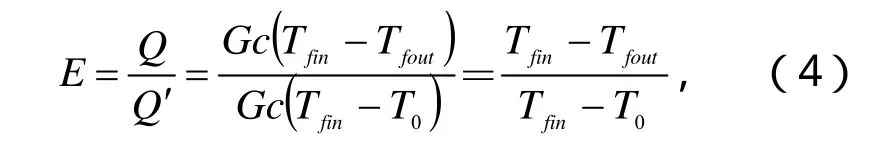
式中Tfin、Tfout、T0分别为U型地埋管换热器进口温度、出口温度、土壤初始温度；G、c分别为埋管内循环介质的质量流量、比热容。

地埋管能效系数是一个无量纲数，其取值范围为0～1，它表征了U型地埋管与周围土壤换热后管中循环介质出口温度能够达到的最低或最高的能力，是传热能力质的特征体现，与地埋管换热器的设计参数相关。当地埋管换热器失去工程意义上的换热能力时，地埋管能效系数E＝0；若地埋管换热器的出口温度能够无限接近土壤初始温度，实际换热量就达到最大理论换热量，此时地埋管能效系数E＝1。

根据能效系数定义和地埋管流体出口温度表达式，有：

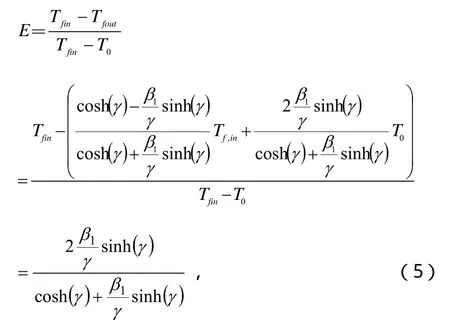
由式（5）可知，地埋管换热器能效系数只与U型地埋管的传热热阻有关，而与进口循环介质温度、土壤初始温度无关。具体来说，钻井能效系数与钻井内埋管的结构尺寸、回填材料的导热系数、U型管材的导热系数、管内循环介质的流量及比热容等有关。在埋管与钻井的结构及热物性参数一定时，钻井的能效系数只与管内循环介质的热容量有关。因此，钻井与土壤（包括埋管、钻井、回填材料及其周围的土壤）的结构、物性以及运行时间决定了地埋管能效系数E的大小。

2 地埋管传热特性及其影响因素分析

2.1 地埋管传热特性分析

为分析地埋管与周围土壤换热过程中传热特性，采用表1所示的基本计算条件对地埋管传热过程进行模拟。

图1表示多极理论传热模型的地埋管换热器能效系数随时间变化情况，模拟运行工况条件如表1所示。

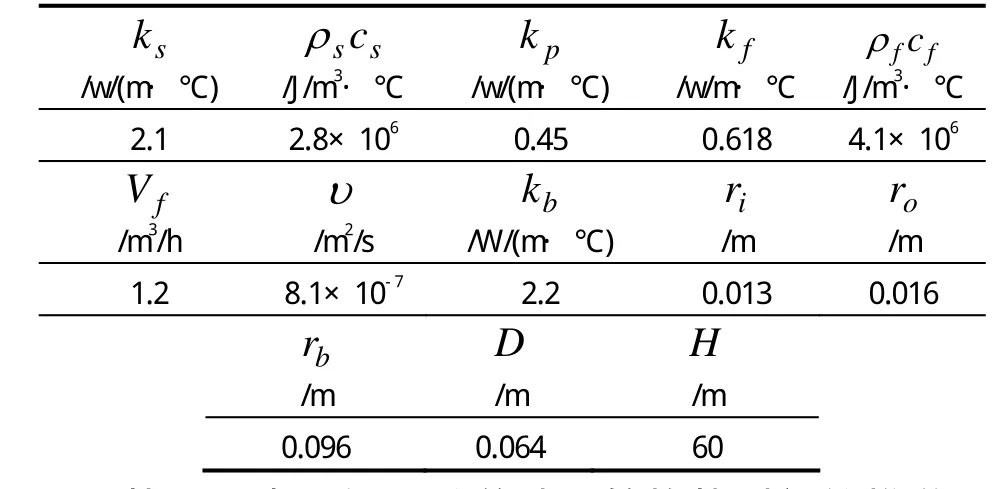
表1 模拟计算条件

从图1中可知，随着地埋管换热时间的推移，地埋管换热器能效系数逐渐减小，变化逐步趋于平缓。在地埋管初始运行时，地埋管内循环介质与周围土壤换热较少，土壤热堆积效应作用较弱，地埋管能效系数较高，出口温度相对较低或较高，地埋管循环介质流量一定时换热量较高。但能效系数并不是趋近于1，而是0.38，这主要是由于钻井内部采用稳态传热分析以及多极理论传热模型计算过程中地埋管内循环介质温度在初始阶段与地埋管进口温度相一致，埋管出口温度并不等于土壤初始温度，能效系数相应地就不是很大。随着换热时间的增加，地埋管与周围土壤的换热过程热堆积效应逐渐增加，温变热阻越来越大，地埋管能效系数逐步减小，循环介质出口温度就逐步升高，地埋管换热量逐步减少，最后这些变化趋于缓慢。由此可见，在一定的地埋管换热器设计结构条件下，如果热泵主机的进口温度冬季要求较高，夏天较低，地埋管则只能运行一定的时间，否则主机运行效率不高，地埋管换热效率低。

2.2 地埋管传热特性影响因素分析

下面将基于以上建立的地埋管传热模型，对影响垂直U型埋管换热特性的各特性参数进行了分析。

2.2.1 回填材料的影响

图2表示在不同的钻井回填材料物性条件下埋管换热器能效系数随时间变化情况。模拟运行工况是回填材料导热系数kb分别为8.7 w/m·℃、6.8w/m·℃、2.2 w/m·℃、1.4 w/m·℃，其他计算条件详见表1。

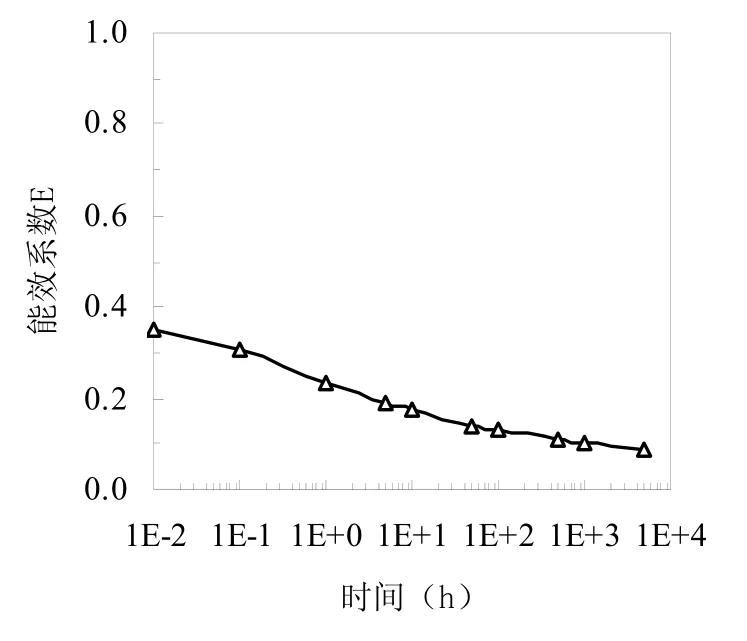
图1 地埋管换热器能效系数变化曲线

从图2中可以看出，回填材料的导热性能对地埋管换热器全局能效系数的影响随时间的不同而不同。地埋管换热器中与周围土壤进行换热初期，此时埋管周围的土壤无热量堆积作用，回填材料导热能力越强，地埋管能效系数越大。随着传热时间的增长，周围土壤堆积了大量的热量需向四周扩散，热堆积效应越大，此时回填材料较强的传热性能反而加大了两支管间的传热，热短路作用增强，导致地埋管能效系数迅速减小。特别是在地埋管运行时间到5000小时左右，四种导热能力的回填材料地埋管换热器能效系数已相差无几，而在地埋管运行时间越短，这种差异更加明显，这说明加大回填材料的导热能力可以不同程度削弱或抵消埋管周围土壤的热堆积作用，但运行时间一长，效果就很难体现。工程设计中应根据运行时间间歇大小和经济性选取回填材料。

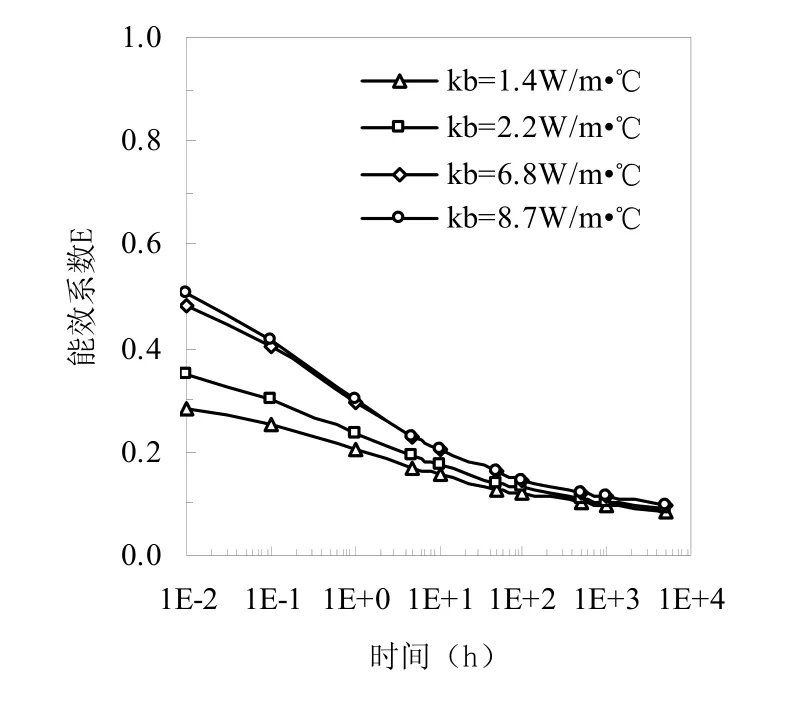
图2 回填材料物性对地埋管能效系数的影响

当然，高导热能力的回填材料肯定是有助于地埋管与土壤间的传热，但是选择回填材料时应根据现场地质条件和运行工况，并不能以导热系数的高低为唯一标准。这主要考虑到两个方面的原因，一方面实际工程中回填材料的选取受到经济性和技术的影响，另一方面是回填材料的急剧增加并不能够促使地埋管换热器传热性能的快速提高，不经济，如在地埋管运行时间为50小时，回填材料导热系数从2.2w/m·℃变化到6.8 w/m·℃，导热系数增加209.1%，而能效系数值只增加了12.9%，而回填材料导热系数从1.4w/m·℃变化到2.2 w/m·℃，导热系数增加57.1%，而能效系数值能够增加9.26 %。应该根据现场土壤地质条件选择合适的回填材料，增强地埋管换热能力。

2.2.2 支管间距的影响

图3表示保持钻井尺寸不变时在不同支管间距条件下埋管换热器能效系数随时间变化情况。模拟运行工况是支管间距2D分别为11ro、8ro、5ro，其他计算条件详见表1。

从图3中可看出，在不同支管间距条件下地埋管能效系数变化趋势相一致，是随着换热时间的增加逐步减小的。在地埋管运行初期，支管间距越大，地埋管能效系数越高，这主要是由于支管间距越大有助于减小两支管间的热短路作用，提高换热效率。随着埋管换热时间的不断增长，埋管周围土壤的热堆积效应增强，能效系数逐步下降，但支管间距较大者的能效变化曲线始终位于较小者之上，只是差距越来越小。进一步分析可知，随着U型管支管间距的增大，地埋管能效系数的增幅减小，这说明在钻井结构尺寸一定的条件下，支管间距的选择有一定的限度，在实际工程中应根据空调系统运行时间规律设计埋管间距，即连续运行可经济性选择，间歇运行可设计较大的支管间距。

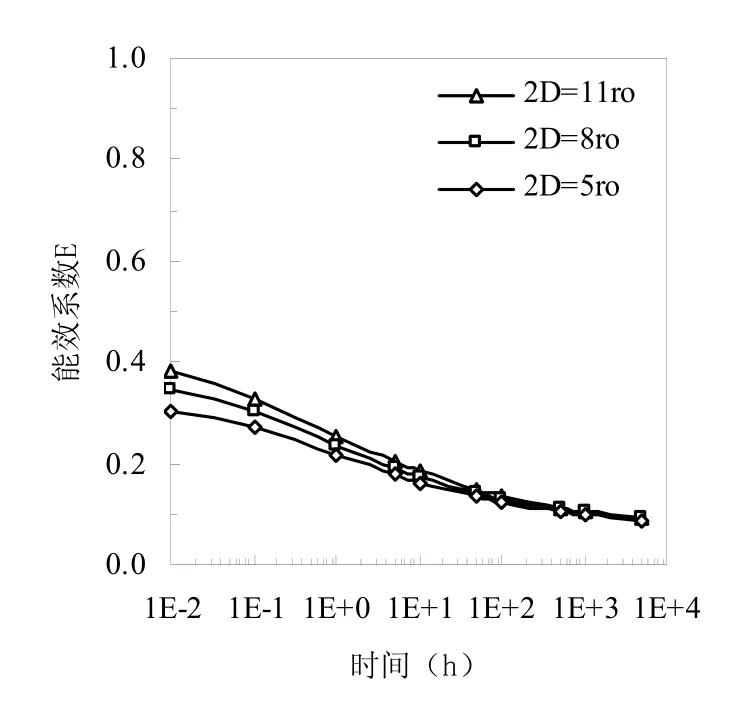
图3 支管间距对地埋管能效系数的影响

2.2.3 埋设深度的影响

图4表示在不同地埋管埋设深度条件下埋管换热器能效系数随时间变化情况。模拟运行工况是埋设深度分别为60m、80m、100m，其他计算条件详见表1。

从图4中可看出，在不同埋设深度条件下地埋管能效系数随时间增加的整体变化趋势一致，但深度的大小对传热特性有着不同的影响。埋设深度越大时，地埋管能效系数越大，地埋管总的换热能力就越高，而对于工程中常用的衡量地埋管换热能力的单位井深换热量却不一定增大。这是因为地埋管的单位深度换热量是由单U型管总换热量与钻井深度共同决定的，而当其中一方减大而另一方也增大时就需要综合考虑两者之间的关系。

单位井深换热量qH可按以下公式计算：

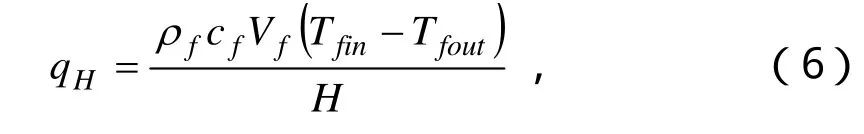
式中，fρ、cf分别为循环介质的密度、比热；Vf为循环介质流量；Tfin、Tfout分别为地埋管进出口温度；H为地埋管埋设深度。

经过分析，可以发现，对于地埋管换热量而言，并非地埋管埋设深度简单地取值为越大或越小，地埋管的换热能力就越强，而是有一个最佳埋设深度，称为“最佳经济深度”，对应于地埋管合理的换热量和初投资。“最佳经济深度”取值总的原则是，一方面埋设深度大一些，使地埋管出口温度满足热泵主机高效运行；另一方面该深度又不宜过大，以控制地埋管钻井所需初投资费用在合理的范围内，一般的推荐值为40～100m，这样两方面都可以兼顾，既可以加大换热量又不过度增加初投资。

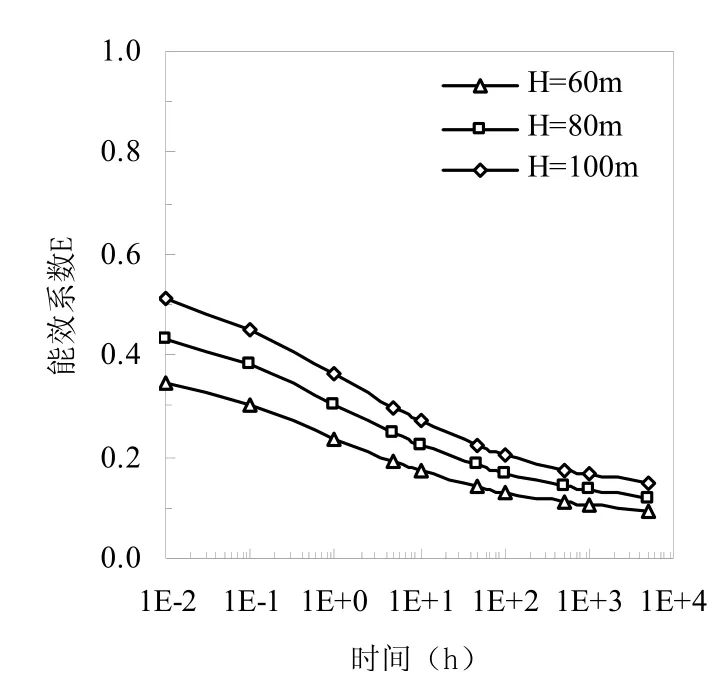
图4 埋设深度对地埋管能效系数的影响

2.2.4 土壤物性的影响

图5、图6表示在不同土壤物性条件下埋管换热器能效系数随时间变化情况。模拟运行工况是土壤导热系数ks分别为1.3 w/m·℃、2.1w/m·℃、3.0 w/m·℃，土壤体积热容ρscs分别为3.42× 106J/m3·℃、2.77×106J/m3·℃、2.37×106J/m3·℃，其他计算条件详见表1。

从图5、图6中可以看出，随着传热时间的增加，不同土壤物性工况下地埋管能效系数均逐步减小，变化趋于平缓，在此过程中土壤物性中导热能力对地埋管传热特性的影响很明显，而土壤热容量对地埋管传热过程影响很小。

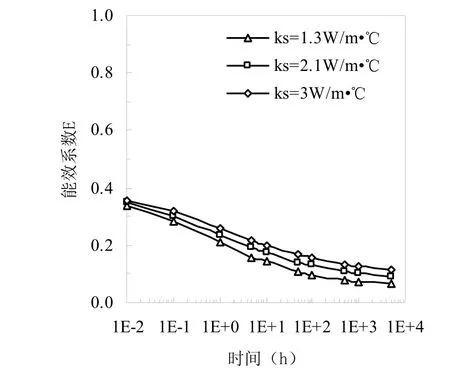
图5 土壤导热系数对地埋管能效系数的影响

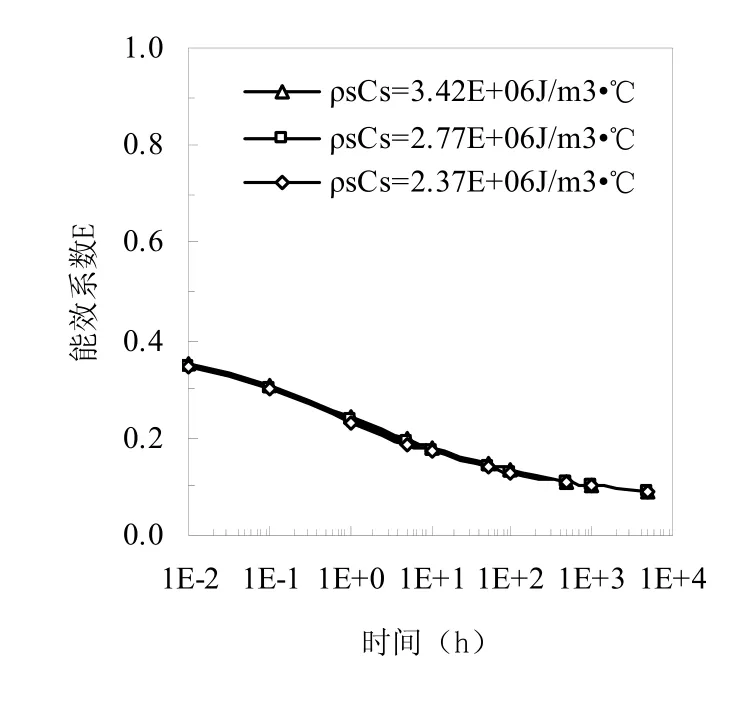
图6 土壤体积热容对地埋管能效系数的影响

图5表示的是地埋管能效系数在土壤导热能力影响下的变化情况。在地埋管换热初期，热量传递过程仅局限于钻井内部和很小一部分钻井外土壤区域，因而土壤的导热能力对地埋管的换热过程影响很小，三种导热系数的土壤能效系数相差甚微。随着时间的增长，钻井外土壤导热能力对换热过程的影响作用逐步增强，三者的换热效率出现差异，导热能力越强的土壤对应的地埋管传热性能越高，其能效系数变化曲线位于上面。在换热时间为0.1小时时刻，土壤导热系数从1.3 w/m·℃增加到2.1w/m·℃时，能效系数相差0.09；而换热时间为500小时两者能效系数相差0.29。由此可见，土壤导热能力高有助于强化地埋管内循环介质与周围土壤之间的热量传递，在地埋管换热负荷一定的条件下，可以减小钻井和埋设地埋管的初投资，有利于土壤源热泵系统的进一步推广应用。

2.2.5 循环介质流速的影响

图7表示在不同埋管内循环介质流速条件下埋管换热器能效系数随时间变化情况。模拟运行工况是循环介质流速分别为0.838m/s、0.628m/s、0.419m/s，其他计算条件详见表1。

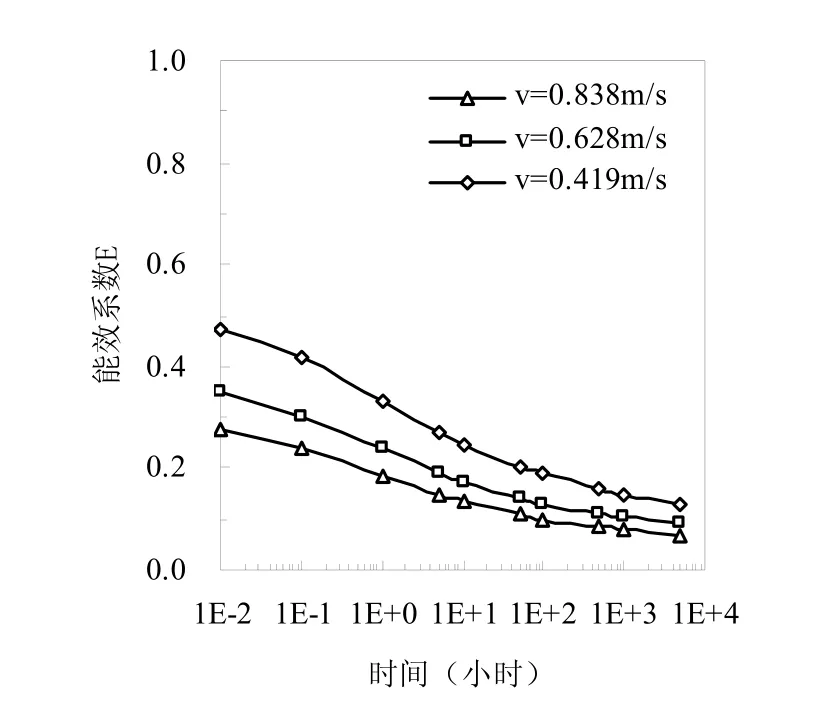
图7 循环介质流速对地埋管能效系数的影响

从图7中可看出，在不同循环介质流速条件下地埋管能效系数随时间增加的整体变化趋势一致，但流速的大小对传热特性有着不同的影响。流速越小时，地埋管能效系数越大，进出口温差相应的增大，这对土壤源热泵主机的运行效率是很有利，但这不意味着地埋管的换热能力就越高，这是因为地埋管的换热能力由进出口温差和流量的乘积共同决定，而当其中一方减小而另一方增大时就需要综合考虑两者之间的关系。

U型地埋管换热量Q可按以下公式计算：

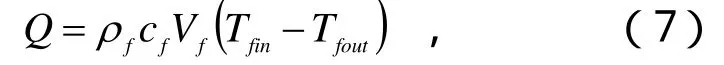
式中，fρ、cf分别为循环介质的密度、比热；Vf为循环介质流量；Tfin、Tfout分别为地埋管进出口温度。

经过分析，可以发现，对于地埋管换热量而言，并非管内循环介质流速简单地取值越大或越小，地埋管的换热能力就越强，而是有一个速度平衡点，称为“最佳经济速度”，对应于地埋管合理的换热量和运行费用。“最佳经济速度”取值总的原则是，一方面埋管中的流速应大一些，使管中产生湍流以利于传热；另一方面该流速又不宜过大，以控制循环泵的功率在合理的范围内，一般的推荐值为0.6～1.0m/s，这样两方面都可以兼顾，既可以加大换热量又不增加运行费用。

3 结语

地埋管换热器与土壤之间的热量传递过程研究一直是土壤源热泵系统的技术难点，同时也是该项研究的核心和应用的基础，而建立较为准确的地埋管传热模型是优化换热的关键。本文基于地埋管轴向流动多极理论传热模型并通过引入地埋管传热能效特性参数——能效系数定义分析地埋管与周围土壤传热过程。利用传热模型对不同的回填材料物性、支管间距、地埋管埋设深度、土壤物性、管内循环介质流速条件下地埋管传热过程进行动态模拟，得出了各重要特性参数的变化对U型地埋管传热特性的影响规律。结果表明，增加土壤与回填材料的导热能力、加大支管间距与钻井深度以及管内循环介质流速可以增大能效系数，增强地埋管换热效果。但从经济的角度而言，回填材料导热系数、钻井深度以及管内循环介质流速不能无限制增加，其大小受到地埋管初投资的影响，可根据实际情况进行优化分析，为土壤源热泵地埋管换热器的实际设计提供参考。为了充分发挥土壤源热泵的能效，实际设计应该考虑地埋管、热泵主机及空调区域负荷三者间的相互匹配。

[1] Bose J E, Parker J D, McQuiston F C. Design/data manual for closed-loop ground-coupled heat pump systems[R]. Oklahoma: Oklahoma State University, 1985. 105-108.

[2] Caneta Research Inc. Commercial/institutional Ground -Source Heat Pump Enginnering Manual[M]. Atlanta: ASHRAE, 1995. 568-572.

[3] Mei V C and Baxter V D. Performance of a ground-coupled heat pump with multiple dissimilar U-tube coils in series[J]. ASHRAE Transactions, 1986, 92 (2): 22-25.

[4] Yavuzturk C, Spitler J D and Rees S J. A transient two-dimensional finite volume model for the simulation of vertical U-tube ground heat exchangers[J]. ASHRAE Transactions, 1999, 105(2): 465-474.

[5] Bokanowski Olivier, Lemou Mohammed. Fast multipole method for multivariable integrals [J]. SIAM Journal on Numerical Analysis, 2005, 42(5): 2098-2117.

[6] Rudberg E, Salek P. Efficient implementation of the fast multipole method [J]. Journal of Chemical Physics, 2006, 125(8): 84-106.

[7] 於仲义，胡平放，袁旭东.含偏心热源同轴多层圆柱稳态温度场分析[J]. 华中科技大学学报（城市科学版）, 2008, 25(3): 162-165.

[8] Sutton M, Nutter D, Couvillion R et al. Comparison of multilayer borefield design algorithm (MLBDA) to available GCHP benchmark data [J]. ASHRAE Transactions, 2002, 108(2): 82-87.

[9] Bandyopadhyay A K, Tomassoni C, Mongiardo M et al. Generalized multipole technique without redundant multipoles [J]. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 2005, 18(6): 413-427

[10] Sutton M, Nutter D, Couvillion, R. A ground resistance for vertical bore heat exchangers with groundwater flow [J]. ASME Journal of Energy Resources Technology, 2003, 125(3):183-189.

[11] Eskilson P, Claesson J. Simulation model for thermally interacting heat extraction boreholes [J]. Numerical Heat Transfer, 1988, 13(2):149 –165.

[12] Hellstrom G. Ground heat storage, thermal analysis of duct storage systems [D]. Sweden: Lund University, 1987.

[13] 於仲义，胡平放，袁旭东. 基于多极理论的U型地埋管轴向流动传热模型研究[J]. 太阳能学报，2009, 29(2): 184-186.

[14] 丁力行, 陈季芬, 彭梦珑. 土壤源热泵垂直单埋管换热性能影响因素研究[J]. 流体机械, 2002, 30(3): 47-49.

[15] 刘宪英, 胡鸣明, 魏唐棣. 地热源热泵地下埋管换热器传热模型的综述[J]. 重庆建筑大学学报. 1999, (4): 106-111

[16]於仲义, 胡平放, 袁旭东. 地埋管地源热泵地埋管换热器传热机制研究[J]. 煤气与热力, 2008, 28(12): 07-11.

[17]於仲义, 胡平放, 徐玉党, 等. 基于换热能效度的竖直地埋管埋设深度设计[J]. 暖通空调, 2009, 39(3): 98-101.

Study on Heat Transfer Characteristic of Vertical U-shape Ground Heat Exchangers Based on Multiple Theory of Heat Transfer

YU Zhong-yi1, CHEN Yan-hua1, HU Ping-fang2, YUAN Xu-dong2

(1 Wuhan Architectural Design Institute, Wuhan Hebei 430074, China;
2 Department of Building Environment and Equipment Engineering, HUST, Wuhan Hubei 430074, China)

The outlet temperature of cyclic medium through ground heat exchangers (GHEs) not only reflects heat transfer capacity of GHEs, but also greatly affects operational efficiency of heat pump units. It is an important characteristic parameter of heat transfer process for GHEs and can be denoted by introducing energy efficiency coefficient. Based on multiple theory model of heat transfer for GHEs in soil, a dynamic simulation is conducted to analyze the heat transfer process under different circumstances including backfill material properties, distance between tube legs, buried depth of ground heat exchangers, soil heat properties and flow velocity of cyclic medium. The influence of important characteristic parameters on the heat transfer performance of vertical U-shape GHEs can be thus achieved, which may provide references for ground source heat pump GHEs in practical designs.

ground source heat pump (GSHP); ground heat exchanger (GHE); energy efficiency; coefficient multiple theory; heat transfer model

TK124

A

1009－5160(2010)03－0016－06

於仲义（1977-），男，博士，高级工程师，研究方向：地源热泵技术研究和设计.

国家自然科学基金项目（50578067）.