Application of unscented Kalman filter in identification of INS error parameters based on centrifuge test

SU Bao-ku, CHEN Cai, GUO Gang

(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China)

Application of unscented Kalman filter in identification of INS error parameters based on centrifuge test

SU Bao-ku, CHEN Cai, GUO Gang

(Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin 150001, China)

Abstract：In order to identify the error parameters of inertial navigation platform in the centrifuge testing, a non-linear model of INS for the identification with a direct method is established. According to the actual system model, the standard unscented Kalman filter(UKF) algorithm is simplified and improved. Compared with the standard UKF, the improved algorithm has the same filtering precision, simpler configuration and lower calculation load. An extended Kalman filter(EKF) algorithm and the improved UKF algorithm are applied respectively to identify the error parameters of INS based on centrifuge test. The simulation results demonstrate that the improved UKF algorithm is more precise in INS error parameter identification and easier to implement than EKF algorithm.

Key words：inertial navigation platform; nonlinear filtering; parameter identification; unscented Kalman filter algorithm

The inertial navigation system (INS) is the key component of navigation system, and its precision is mainly decided by the inertial measuring instruments’ precision[1]. Generally, there are two approaches for improving the INS precision: the first way is to increase the inertial measuring instruments’ precision, however, their research cost is too high; the other one is to establish the error model of the INS, then identify their error parameters, which can be used to compensate the precision of the INS, through laboratory testing. Obviously, the second way is more economical and effective in improving the INS’s precision .

In fact, the error model of an INS is a nonlinear model. And the most common application of nonlinear estimation algorithm is the Extended Kalman filter (EKF), which simply linearizes all nonlinear models based on Taylor series approximation[2]. However, linearization usually introduces significant biases or errors in practice. The EKF can also be prohibitively difficult to implement because deriving Jacobian matrices can be error-prone and time consuming (especially when the system is complicated and of high order)[3].

To overcome those limitation of EKF, an Unscented Kalman filter (UKF) was developed by Julier and Uhlmann[4]. The UKFuse the unscented transformation to propagate mean and covariance information through nonlinear transformations. The advantage of unscented transformation over the Taylor series based approximation is that unscented transformation is better at capturing the higher order moments caused by the nonlinear transform, as discussed in Ref.[5]. In addition, the Jacobian matrices are not needed, so the estimation procedure is easier and less error-prone. Compared with EKF, the UKF is more accurate, easier to implement, and uses the same order of calculations as EKF.

In this paper, we establish the system model of INS with a direct method, then simplify the standard UKF and improve the filter algorithm according to the properties of the system model. The improved UKF algorithm and the EKF are applied to identify the error parameters of INS based on centrifuge testing. Those identification results are compared in the simulation section.

1 System Mathematical Models

In this paper, the identification for the error parameters of INS is based on the centrifuge testing. In order to avoid the linearization for nonlinear state equations, we use the direct method to establish system model[6].

1.1 Error model of the INS

In order to achieve the desired modeling accuracy without unnecessarily increasing the complexity of the model, it was determined that 18 unknown parameters for the INS are needed[7]. Then the error model of the INS is given as follows:

where

K0are unknown accelerometer biases, and K1are unknown accelerometer scale factors;

D0are unknown gyro fixed drift, and D1are unknown gyro mass unbalance parameters;

A0are applied accelerations along each axes.

1.2 State and measurement equations

In the identification program, the objective is to obtain the estimates of INS unknown parameters. Therefore, all the unknown parameters in equation (1) are defined as state variables. In addition, three Euler angles(α, β, γ) that represent the system dynamic motion of the INS are also defined as state variables. Then the state variables for error parameters identification of INS based on centrifuge testing can be defined as follows:

The nonlinear state vector equation of the INS for the identification program is given as follows:

Furthermore, we take the output of three accelerations in the INS as the output measurement.

And the measurement equation is based on the INS acceleration model in equation (1)[8].

The state and measurement equations are in continuous form, but the measurements are obtained at discrete time points. Therefore, we should discretize equation (2) and (3) so that we can develop the filter equations using the discrete form of filter algorithm.

2 Design of Filtering Algorithm

2.1 The standard UKF algorithm

Consider a discrete nonlinear system described as follows:

A standard UKF consists of the following steps:

Step 1:Set the initial values for state meanand error covariance P0. Then form the disturbance process and the measurement noise vectors into the augmented state variables as follows:

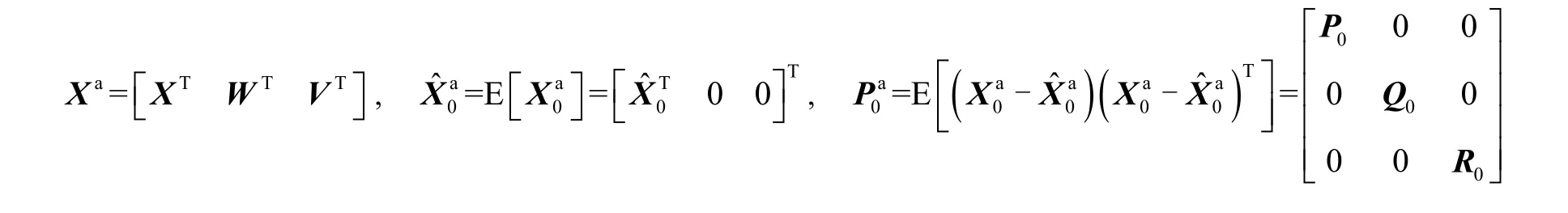
Step 2:Compute the matrix of sigma points for the augmented system and calculate the relevant weights, which are defined as follows:

Step 3:Compute the predicted state mean and the predicted covariance as:

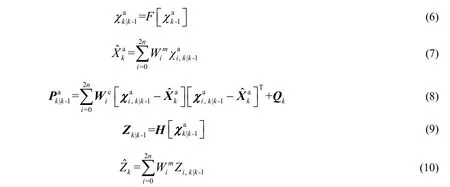
Step 4:Update state mean and error covariance as:

2.2 The improved UKF algorithm

We can find that all the disturbance process and the measurement noise vectors are augmented as the state variables in the standard UKF. And the dimension of the augmented state matrix is much larger than that of the original state variable, which will cause lots of calculation for the filter.

Fortunately, the disturbance process and the measurement noise discussed in this paper are additive for the system, which means the augment process for the state variables is not necessary. In addition, the measurement equation for the system is a linear one. Therefore, we can simplify the standard UKF and improve the filter algorithm as follows:

1) Maintain the number of state variables without augment process;

2) Rewrite the equation (9) as

Then substitute equation (16) into equation (11) and (12). Finally, we can get the improved UKF algorithm.

3 Simulation Results

This section applies and compares the performance of the improved UKF against an EKF for the parameters identification of INS based on centrifuge testing. In this simulation, we assume that the applied acceleration provided by centrifuge rotation is 10g level, where g represents local gravity acceleration. The axes of INS are aligned with the east, north, and up directions. The rotation radius of the centrifuge is 2.5 m, so the rotation angular rate of the centrifuge is 2π rad/s. The measurement cycle is 0.04 s, and the simulation time is 800 s. The simulation results are shown in Fig.1 and Fig.2, where REF represents the reference values of those unknown parameters for INS.

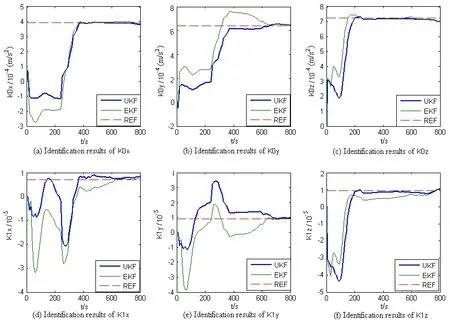
Fig.1 Identification results of INS accelerometer parameters

The simulation results show that the improved UKF is better than EKF in estimating those unknown parameters of INS because the EKF linearization for the INS nonlinear model introduces biases or errors to the system, while the UKF overcomes this drawback with the unscented transformation. Moreover, the UKF uses the same order of calculations as EKF.

Fig.2 Identification results of INS gyro parameters

4 Conclusion

The UKF is a simple and efficient approach for solving linear and nonlinear problems. Compared with EKF, the UKF is more accurate and easier to implement because it does not involve any linearization steps, eliminating the derivation and evaluation of Jacobian matrices. Meanwhile, it uses the same order of calculations as EKF.

In this paper we establish the system model of INS with the direct method, then simplify the standard UKF and improve the filter algorithm according to the practical system model. The simulation results demonstrate that the improved UKF algorithm can improve the identification precision of INS error parameters.

[1] Wang H G, Williams T C. Strategic inertial navigation systems-high-accuracy inertially stabilized platforms for hostile environments [J]. IEEE Control Systems Magazine, 2008, 28(1): 65-85.

[2] Romanenko R, CasLro J. The unscented filler as an alternative to the EKF for nonlinear state estimation: A simulation case study [J]. Computers and Chemical Engineering, 2004, 28(3): 347-355.

[3] Julier S, Uhlmann J, Durrant-Whyte H F. A new method for the nonlinear transformation of means and covariance in filters and estimators[J]. IEEE Transactions on Automatic Control, 2000, 45(3): 477-482.

[4] Julier S, Uhlmann J. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE Aerospace and Electronic Systems, 2004, 92(3): 401-422.

[5] 杨波，秦永元，柴艳. UKF在INS/GPS直接法卡尔曼滤波中的应用[J]. 传感技术学报，2007，20(4)：842-846. YANG Bo, QIN Yong-yuan, CAI Yan. Application of UKF in direct method of Kalman filter for INS/GPS[J]. Chinese Journal of Sensors and Actuators, 2007, 20(4): 842-846.

[6] IEEE recommended practice for inertial sensor test equipment, instrumentation, data acquisition, and analysis[S]. IEEE Std 1554TM-2005.

[7] Frazier J H. Application of extended Kalman filtering to a dynamic laboratory calibration of an inertial navigation system[R]. 1973, AD 763718: 109-175.

[8] 张敏虎，任 章，华春红. UKF在深组合GPS/INS导航系统中的应用[J]. 中国惯性技术学报，2009，17(6)：697-700. ZHANG Min-hu, REN Zhang, HUA Chun-hong. Application of UKF in deeply coupled GPS/INS navigation system[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 697-700.

UKF在惯导平台误差系数辨识离心机测试中的应用

苏宝库，陈 才，郭 刚
（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

针对惯导平台误差系数辨识的离心机测试，利用直接法建立了误差系数辨识的非线性模型，并结合实际系统模型的特点对标准UKF算法进行了简化和改进。改进后的UKF结构简单，与标准UKF具有同样的滤波精度，并且减小了计算量，提高了计算效率。然后利用扩展Kalman滤波（EKF）算法和改进的UKF算法对惯导平台误差系数辨识离心机测试进行仿真。结果表明，与EKF算法相比，改进的UKF算法能提高惯导平台误差系数的辨识精度，并且更容易实现。

惯导平台；非线性滤波；参数辨识；UKF算法

U666.1

A

1005-6734(2010)03-0382-05

2010-01-18；

2010-02-18

国家安全重大基础研究项目(973－61334)

苏宝库（1941—），男，教授，博士生导师。 E-mail：subk@hit.edu.cn