基于偏好信息区间权重的求解

兰继斌，韦晓静，王艳青，黄燕革

（1.广西大学 数学与信息科学学院，广西 南宁 530004；2.百色学院 数学与计算机科学系，广西 百色 533000）

基于偏好信息区间权重的求解

兰继斌1，韦晓静1，王艳青1，黄燕革2

（1.广西大学 数学与信息科学学院，广西 南宁 530004；2.百色学院 数学与计算机科学系，广西 百色 533000）

在Saaty所定义的一致性条件下，提出一种含有参数的互反判断矩阵元素与权重的逻辑关系，并对参数进行说明同时得到一些重要的结论.然后把所提的逻辑关系推广到区间互反判断矩阵，建立数学模型得到使决策者满意的区间权重.最后通过例子加于说明.

偏好信息；区间判断矩阵；权重

层次分析法作为一种决策工具，已被广泛的应用在各个领域.对于给定的实互反判断矩阵求解权重的方法很多学者都做了深入的研究，例如被用得最为广泛的特征向量法 （EM），以及最小二乘法（LSM）等等.由于决策者的不确定性和事物本身固有的复杂性，利用模糊数或区间数反映决策者的偏好更为合理.对如何从区间互反判断矩阵中求出权重，不少学者也对此进行了探讨，文献[1-11]给出了不同的方法求解区间权重.无论是实互反判断矩阵还是区间互反判断矩阵，判断矩阵一旦确定相应的权重也就确定.但是每个人的偏好是不一样的，即使是对同一个互反判断矩阵，不同的决策者得到的权重应该是不一样的，因此我们有必要在求解权重时加入决策者的偏好信息.本文提出一个含有参数的元素和权重逻辑关系，并把这个逻辑关系推广到区间判断矩阵，由此建立模型求解出使决策者满意的权重.

1基本概念及新的逻辑关系

设 A={A1，A2，…，A3}为备选方案集，记 I={1，2，…，n}.决策者依据某准则C对A中的方案两两进行重要性比较，构造判断矩阵，

定义 1.1［1］设矩阵，其中，若aij满足以下条件：

由结论可知选取的参数θ不同得到的权重也不同，但是它们的序关系并没有发生变化.我们可以把参数θ看成是决策者的偏好信息，对于不同的决策者我们可以选择相应的参数θ得到使决策者得到满意的权重.

于是由 A= （aij）n×n为一致正互反判断矩阵的定义，有

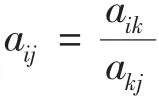
这表明正互反判断矩阵 A= （aij）n×n具有一致性.

结论：

解（M-1）和（M-2）得到权重向量为：

以物质形式存在的传统文化就是说传统文化是看得见摸得着的实体，能够被人们所观摩或者学习的。比如剪纸、古诗词、青花瓷等等，这些传统文化在历史的长河中，人为地或者通过某种形式遗传下来，现在的人能够看到它们的存在，能够供我们研究历史的一些实物，这种类型的文化是难能可贵的。

（2）对于同一个判断矩阵，权重向量为一族权重向量 w（θ） = （w1（θ），…，wn（θ））T，当 θ取不同值时，将会得到不同的权重向量，但不会改变方案的序关系.

其中e是自然对数的底数.

基坑与斜拱桩基承台边缘净距不同时，斜拱桩基产生的水平推力对深基坑的影响是不