On the Asymmetry for Convex Domains of Constant Width∗

JIN HAI-LIN AND GUO QI

(Department of Mathematics,Suzhou University of Technology and Science, Suzhou,Jiangsu,215009)

Communicated by Yin Jing-xue

On the Asymmetry for Convex Domains of Constant Width∗

JIN HAI-LIN AND GUO QI

(Department of Mathematics,Suzhou University of Technology and Science, Suzhou,Jiangsu,215009)

Communicated by Yin Jing-xue

The extremal convex bodies of constant width for the Minkowski measure of asymmetry are discussed.A result,similar to that of H.Groemer’s and of H.Lu’s, is obtained,which states that,for the Minkowski measure of asymmetry,the most asymmetric convex domains of constant width inR2are Reuleaux triangles.

asymmetry measure,reuleaux polygon,constant width

1 Introduction

Measures of(central)symmetry,or as we prefer,asymmetry for convex bodies have been extensively investigated.Among these researches,it is a popular topic to determine the extremal bodies in a class of convex bodies for a given asymmetry measure(see[1]–[2]etc.). Recently,Groemer and Wallen[3]and Lu and Pan[4]determined the extremal bodies in the class of convex domains in R2of constant width,respectively for an asymmetry measure they are concerned with.Concretely,they both showed that the most asymmetric domains are Reuleaux triangles under the concerned asymmetry measure.

In this paper,we prove a similar result for the well-known Minkowski measure of asymmetry.Precisely,the following theorem is obtained:

Theorem 1.1Let K be a convex domain of constant width.Then

where As(·)denotes the Minkowski measure of convex bodies.Equality holds on the left-hand side precisely if and only if K is a circular disc,and on the right-hand side precisely if and only if K is a Reuleaux triangle.

2 Prelimilary

Rndenotes the usual n-dimensional Euclidean space with the canonical inner product〈·,·〉. A bounded closed convex set C⊂Rnis called a convex body(a convex domain for n=2) if it has non-empty interior(int for brief).The family of all convex bodies in Rnis denoted by Kn.Given a convex body C∈Knand a point x∈int(C),for a hyperplane H through x and the pair H1,H2of support hyperplanes of C parallel to H,let r(H,x)be the ratio, not less than 1,in which H divides the distance between H1and H2.Note

and de fi ne the Minkowski measure As(C)of asymmetry of C by(see[3])

A point x∈int(C)satisfying r(C,x)=As(C)is called a critical point(of C).The set of all critical points of C is denoted by C∗.

Thus,if for a given body C∈Rnand an x∈Rn,we de fi ne the support functional of C at x as,for all u∈Sn−1(the(n−1)-dimensional unit sphere),

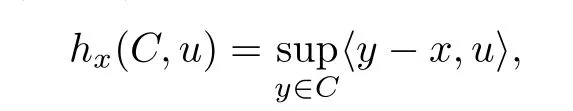
then it is easy to see that

and

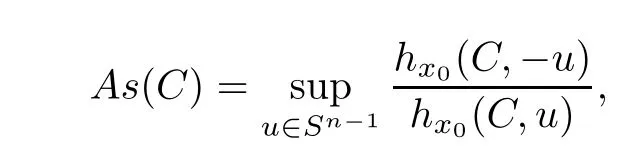
where x0is a critical point of C.

The following is another equivalent de fi nition of the Minkowski measure(see[1]and[5]). Let C∈Knand x∈int(C).For a chord D of C through x,let r1(D,x)be the ratio,not less than 1,in which x divides the length of D,and note that

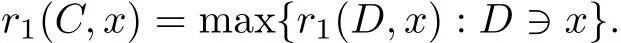
Then

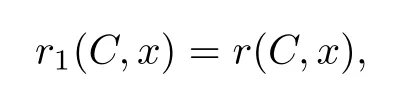
and so the Minkowski measure

A chord D satisfying r1(D,x)=As(C)is called a critical chord(of C).

Note that

SC(x)={p∈bd(C):the chord pq passes through x and satis fi eswhere bd denotes the boundary,and pq denotes the segment with endpoints p,q or its length freely if no confusing is caused.

3 The Minkowski Measure of Regular Reuleaux Polygons

In this section,we discuss the Minkowski measure of regular reuleaux polygons in R2.

Lemma 3.1If a 2-dimensional convex domain C is axially symmetric,then its critical point x must be on the axis.

Proof. Let the domain C be axially symmetric,and x∗be a critical point of C which lies outside the symmetry axis.Then by the axial symmetry,the symmetric point of x∗with respect to the axis must be another critical point.However,the critical point of C is unique (see[5]),a contradiction which completes our proof.

The following corollary follows from Lemma 3.1 directly.

Corollary 3.1The unique critical point of a regular Reuleaux polygon is its centroid.

Next lemma is a generalization of a well-known result in the elementary geometry of R2.

Lemma 3.2and0,then

Proof. Clearly,

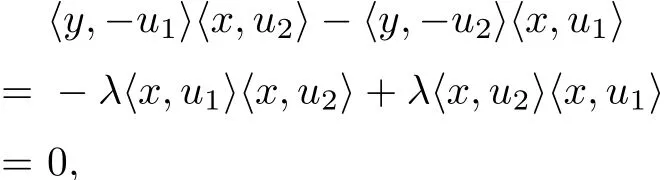
from which the desired result follows.

For a Reuleaux m-polygon with centroid o and vertices

the direction vector of−

e→o.Then we have the following

i

Lemma 3.3Let K be a regular m-Reuleaux polygon with centroid o.Then for any 1≤

Proof. For convenience,we prove the lemma for Reuleaux triangles only.The same argument works for general regular Reuleaux polygon as well.First,clearly

by Corollary 3.1.Then,since,for any 1≤i,j≤3,

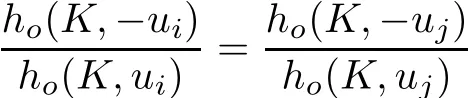
by symmetry,we consider the case i=1 only.

Now we show that for any u∈S1,

Denote by α the angle between u and u1.Then we may consider only such u’s with 0≤α≤for n-polygons)by the symmetry.Notice that,iffor n-polygons),then

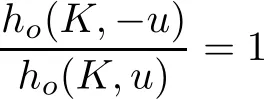
by symmetry.So,by the symmetry again,we may assume for n-polygons) (see Fig.3.1).

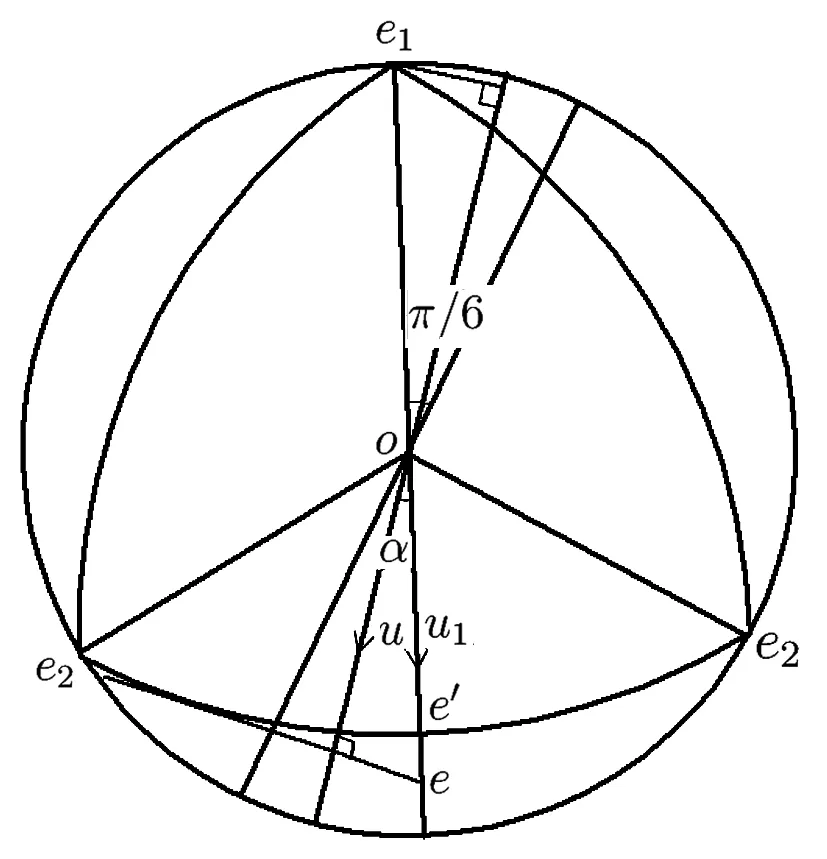
Fig.3.1

It is easy to check by the de fi nition of regular Reuleaux polygons that,for all u∈ S1

which,with the help of Lemma 3.2,gives

The proof is completed.

Next proposition shows the precise values of the Minkowski measure for the regular Reuleaux polygons of order n.

Proposition 3.1Let K be a regular Reuleaux polygon of order n.Then

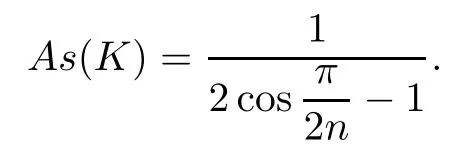
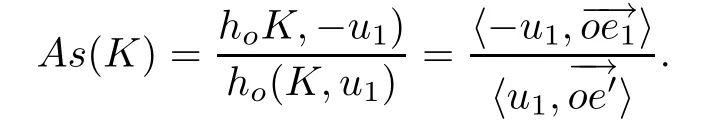
So,we shall fi nish the proof by computing the value of First,it is easy tosee that (see Fig.3.2).

Fig.3.2

By the de fi nition of regular Reuleaux polygons,

and so

The proof is completed.

Corollary 3.2Let K∈K2be a regular Reuleaux polygon of order n.Then

Reuleaux triangle,i.e.,n=3;

Proof. The proof is trival.

4 The Proof of Theorem 1.1

First,we state some lemmas.

Lemma 4.1[5]Suppose x∈ri(C∗)and y∈S(x).ThenC

where ri denotes the relative interior.

This lemma shows that the set SC(p)does not vary as p ranges over ri(C∗).We denote this set by C†.

Lemma 4.2[5]Suppose that C is a convex body in Rn.Then

where dim denotes dimension.And if

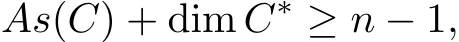
then

where conv denotes the convex hull.

Lemma 4.3[5]C†contains at least As(C)+1 points.

Lemma 4.4[6]Any plane convex body K of constant width ω has area not less thanthe area of a Reuleaux triangle of width ω.

Proof of Theorem 1Let o be the critical point of K.By Lemma 4.3,there exist three critical chordsf3such that

By Lemma 4.2 and the Carath´eodorytheorem,we may assume that o∈int(conAgain by the Theorem 3.2 of[

(notice that K is of constant width),the width of K,which in turn implies that

In the following,we focus on the triangle△e1e2e3only(see Fig.4.1).Without losing generality,we may assume that α≤β≤γ,which clearly implies that α

Fig.4.1

Observe that

which leads to

Hence

So we have proved

For the case that the left-side equality holds,the conclusion is obvious since a centrallysymmetric convex body of constant width must be a circular disc.

For the right-side equality,if K is a Reuleaux triangle,then by Corollary 3.2

Conversely,if

then we must have that

and

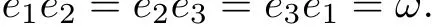
Now we consider the Reuleaux triangle R△generated by the regular triangle△e1e2e3. Since ei∈K(i=1,2,3)and the width of K is ω,K must be contained in the circular disc with radius ω and centered at eifor i=1,2,3.So K ⊂R△.However,by Lemma 4.4,the area of K is not less than the area of R△,so we get that

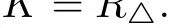
The proof is completed.

[1]Gr¨unbaum,B.,Measure of convex sets,convexity,in:Proceedings of Symposia in Pure Mathematics 7,Amer.Math.Soc.,Providence,1963,pp.233–270.

[2]Besicovitch,A.S.,Measures of asymmetry for convex curves,II.Curves of constant width,J. London Math.Soc.,26(1951),81–93.

[3]Groemer,H.and Wallen,L.J.,A measure of asymmetry for domains of constant width,Beitr¨age Algebra Geom.,42(2001),517–521.

[4]Lu,H.and Pan,S.L.,A measureofasymmetry forconvex domains of constant width,Department of Mathmatics,Eastern China Normal University,preprint,2005-001; http://www.math.ecnu.edu.cn/preprint/2005-001.ps.

[5]Klee,Jr.V.L.,The critical set of a convex set,Amer.J.Math.,75(1953),178–188.

[6]Chakerian,G.D.,Sets of constant width,Paci fi c J.Math.,19(1)(1966),13–21.

52A38

A

1674-5647(2010)02-0176-07

date:Sept.8,2009.

The NSF(08KJD110016)of Jiangsu Hight Education.