Linearly McCoy Rings and Their Generalizations∗

CUI JIAN AND CHEN JIAN-LONG

(Department of Mathematics,Southeast University,Nanjing,210096)

Communicated by Du Xian-kun

Linearly McCoy Rings and Their Generalizations∗

CUI JIAN AND CHEN JIAN-LONG

(Department of Mathematics,Southeast University,Nanjing,210096)

Communicated by Du Xian-kun

A ringRis called linearly McCoy if whenever linear polynomialsf(x), g(x)∈R[x]{0}satisfyf(x)g(x)=0,then there exist nonzero elementsr,s∈R such thatf(x)r=sg(x)=0.For a ring endomorphismα,we introduced the notion ofα-skew linearly McCoy rings by considering the polynomials in the skew polynomial ringR[x;α]in place of the ringR[x].A number of properties of this generalization are established and extension properties ofα-skew linearly McCoy rings are given.

linearly McCoy ring,α-skew linearly McCoy ring,polynomial ring, matrix ring

1 Introduction

Throughout the paper,R denotes an associative ring with identity 1.The notation α denotes an endomorphism of a given ring,and α(1)need not be equal to 1 in this paper.

McCoy[1]proved in 1942 that if two polynomials annihilate each other over a commutative ring,then each polynomial has a nonzero annihilator in the base ring.Rege and Chhawchharia[2]and Nielsen[3]introduced the notion of a McCoy ring,independently.Recall that a ring R is called right McCoy if the equation

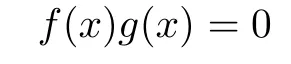
with nonzero f(x),g(x)∈R[x],implies that there exists a nonzero r∈R such that

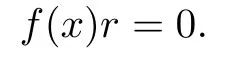
Left McCoy rings are de fi ned similarly.A ring R is said to be McCoy if it is both right and left McCoy.The concept of right(left)linearly McCoy rings were introduced by Camillo and Nielsen[4]in 2008.A linearly McCoy ring is both left and right linearly McCoy.It wasproved in[4]that semi-commutative rings(i.e.,ab=0 implies aRb=0 for a,b∈R)are linearly McCoy,but the converse is not true.

For a ring R with a ring endomorphism α:R→R,a skew polynomial ring R[x;α]of R is the ring obtained by giving the polynomial ring over R with the new multiplication

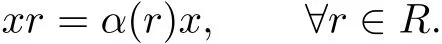
Due to Hong et al.[5],the Armendariz property of a ring was extended to skew polynomial rings but with skewed scalar multiplication:For an endomorphism α of a ring R,R is called α-skew Armendariz if

implies

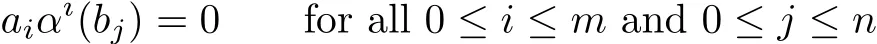
(R is called Armendariz if α=IR).And Lei[6]extended McCoy rings to α-skew McCoy rings.

Motivated by the above,we introduced the notion of an α-skew linearly McCoy ring with the endomorphism α,as both a generalization of α-skew McCoy rings and an extension of linearly McCoy rings.The properties of this class of rings are investigated.

2 Linearly McCoy Rings

Our focus in this section is to discuss the basic properties of linearly McCoy rings and observe the connections to other related rings;extension properties of the rings are investigated.

Lemma 2.1A ring R is right(resp.,left)linearly McCoy if and only if the ring

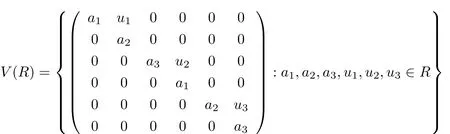
is right(resp.,left)linearly McCoy.

Proof. It suffices to prove the case when R is right linearly McCoy.

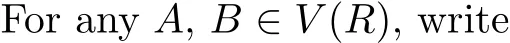
The addition and multiplication in V(R)are de fi ned as follows:

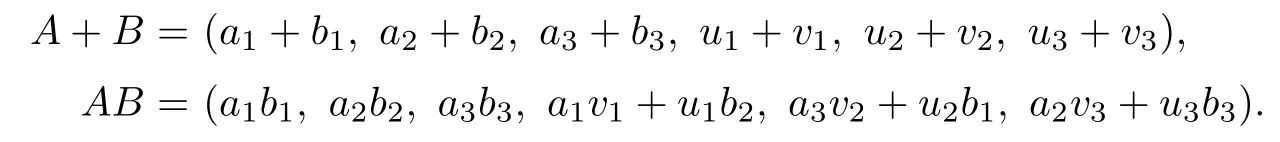
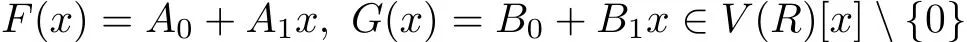
with

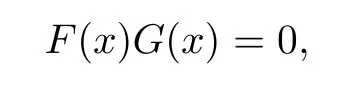
where

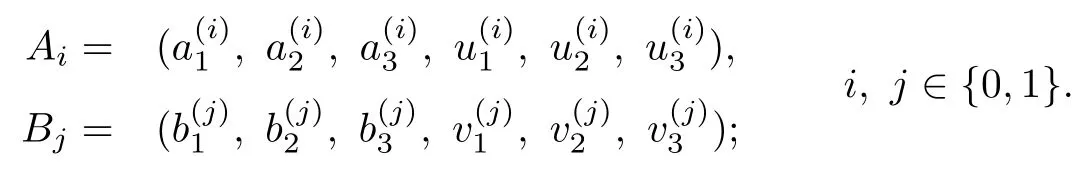
Then

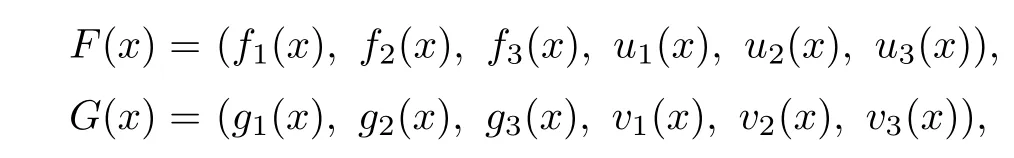
where

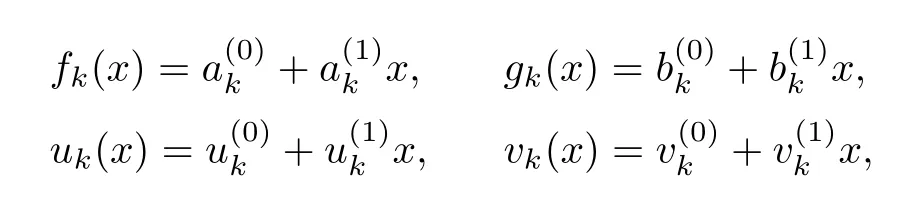
and

Case 1.Suppose that fk(x)=0 for some k.Without loss of generality,let

Then

Write

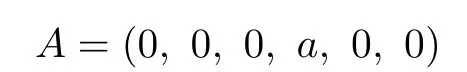
for any nonzero a∈R.Then

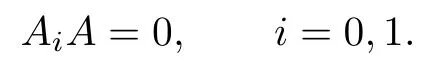
Case 2.Suppose that fk(x)/=0,gk(x)=0 for every k.Since G(x)/=0,there exists some k0such that

We may assume that v1(x)/=0.Then

Since R is right linearly McCoy,there exists a∈R{0}such that

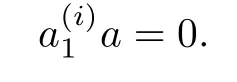
Put

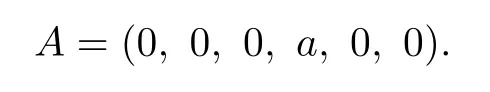
Then,for each i,

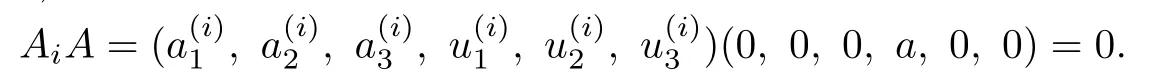
Case 3.Suppose that fk(x)/=0 for all k and gl(x)/=0 for some l.We may assume that g1(x)/=0.Then

As the proof of Case 2,there exists a nonzero A∈V(R)such that

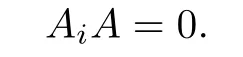
Therefore,V(R)is a right linearly McCoy ring.

“⇐”.Suppose that

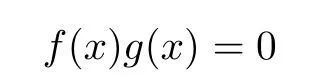
Then

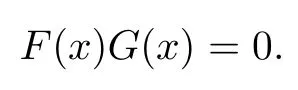
Because V(R)is right linearly McCoy,there exists A∈V(R){0}satisfying

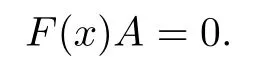
It follows that

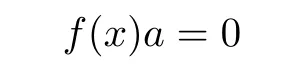
for some nonzero a∈R.Thus R is right linearly McCoy.

The proof is completed.

It is well known that the class of semi-commutative rings or Armendariz rings is closed under subrings.However,for a linearly McCoy ring,we have the following:

Example 2.1Let R=Z4⊕Z4be a commutative ring,where Z4is the ring of integers modulo 4,and denote it by Z4={0,1,2,3}.Consider the ring

V(R)is linearly McCoy by Lemma 2.1.Let

It is easy to check that S is a subring of V(R)under the usual matrix operations.We show that S is not a right linearly McCoy ring.In fact,let

with

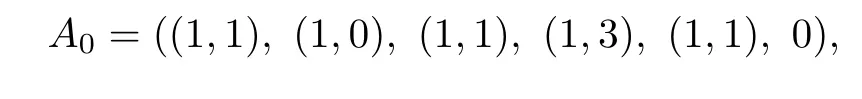
Then

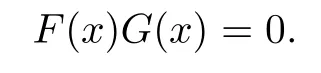
Assume that there exists

such that

Then

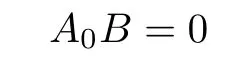
implies that

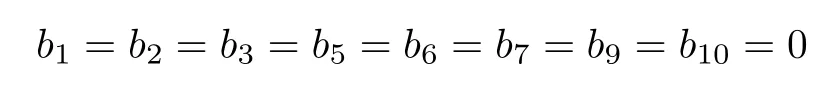
and

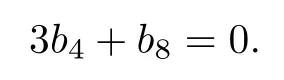
From A1B=0 we obtain

So

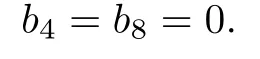
Thus we have B=0,as asserted.

Remark 2.1(1)For Example 2.1,take I={re56:r∈R},with e56the usual matrix unit(with 1 at(5,6)-entry,0 elsewhere).Note that I is an ideal of V(R)and V(R)/I～=S. Thus the homomorphic image of a linearly McCoy ring need not be linearly McCoy.

(2)V(R)is linearly McCoy over a linearly McCoy ring R by Lemma 2.1,but eV(R)e～=is never linearly McCoy by Theorem 2.1 in[7],where

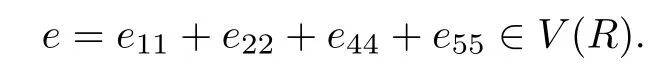
One may suspect that R is linearly McCoy if for any nonzero proper ideal I of R,R/I and I are linearly McCoy,where I is considered as a linearly McCoy ring without identity. However,we provide a counterexample to this situation as follows.

Example 2.2Let F be a division ring and consider the ringThen R is not linearly McCoy by Proposition 10.2 of[4].But by Example 5 of[8],for any nonzero proper ideal I of R,R/I and I are semi-commutative rings,so they are linearly McCoy.

According to Theorem 7.1 in[4],McCoy rings need not be abelian(i.e.,all idempotents are central).The following example shows that the converse does not hold in general.

Example 2.3Let T=Z2〈a,b〉be the free associative algebra over Z2generated by two indeterminates a,b and Z2is the ring of integers modulo 2.Let I=〈a2,b2〉be the ideal of T generated by a2,b2.Let R=T/I.Then R is abelian,but not right linearly McCoy.

We show that R contains no non-trivial idempotents.For any

where giis the monomial in R,we de fi ne the support of r as

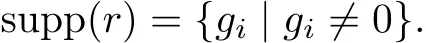
Let e be any nonzero idempotent of R,and suppose 1∈/supp(e).Let e0be the sum of terms with the smallest degree in the support of e.Then e0

/=0.By simple computations we can get

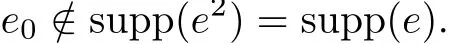
This is a contradiction.Thus 1∈supp(e).

Moreover,let f be any non-trivial idempotent of R.Then

and

but 1/∈supp(1−f),which contradict the discussion above.

Let

Then

Assume that there exists r∈R such that F(x)r=0.Then(ba)r=0 implies r∈aR,and br=0 implies r∈bR.Notice that

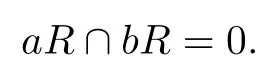
So r=0,and hence R is not right linearly McCoy.

Let T be a subring of a ring S.Set

With addition and multiplication de fi ned componentwise,R[S,T]is a ring.

Proposition 2.1If S is a right linearly McCoy ring with a subring T,then R=R[S,T] is right linearly McCoy.

Proof. Let f,g∈R[x]{0}with fg=0.Write

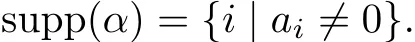
We break the proof into two cases.

Case 1.Assume that there exists some k∈/supp(f).Then for any fi xed a∈R{0},the sequence with a in the k-th coordinate,and 0 elsewhere,annihilates f on the right.

Case 2.Assume that each component of f is nonzero.Then there exists some k∈supp(f)∩supp(g)with fkgk=0.Since R is right linearly McCoy,there exists a∈R{0} such that

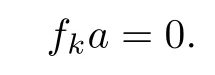
Then the same sequence as in case 1 suffices us.

For an endomorphism α of a linearly McCoy ring R,the following example shows that the skew polynomial ring R[x;α]is not linearly McCoy.We use the ring given in[9].

Example 2.4Let

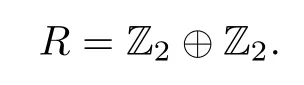
Then R is a commutative ring.Thus it is linearly McCoy.Let α:R→R be an endomorphism de fi ned by

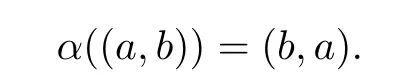
Then for f(x),g(y)∈R[x;α][y]with

one has

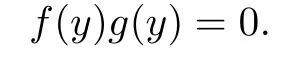
Write

If

then

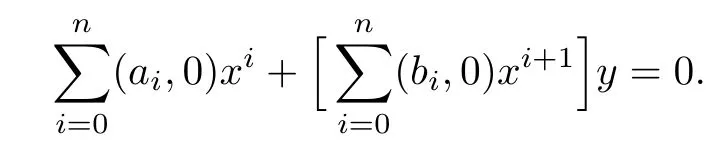
It follows that

Thus R[x;α]is not right linearly McCoy.By a similar proof,we can also show that R[x;α] is not left linearly McCoy.

Proposition 2.2For a ring R and an endomorphism α of R,the following statements hold:

(1)If R[x;α]is right linearly McCoy,then R is right linearly McCoy;

(2) If α is an automorphism and R[x;α]is left linearly McCoy,then R is left linearly McCoy.

Proof. Let

be nonzero polynomials of R[y]with

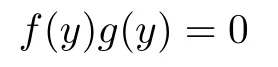
(clearly,f(y),g(y)∈R[x;α][y]{0}).

(1)Assume that R[x;α]is right linearly McCoy.Then there existssuch that

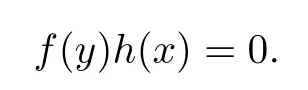
It follows that

Then

for any nonzero coefficient ci0of h(x).Hence R is right linearly McCoy.

(2)By hypothesis,there exists a nonzero polynomialR[x;α]satisfying

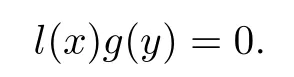
If d0

/=0,then

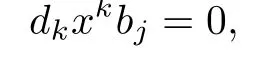
i.e.,

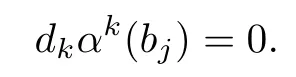
Since α is an automorphism,there existsR{0}such that

Hence

and thus R is left linearly McCoy.

The proof is completed.

Proposition 2.3Let α be an endomorphism of a ring R.Then we have the following:

(1)R is right linearly McCoy if and only if R[x;α]/(xn)is right linearly McCoy;

(2)If α is monic and R is left linearly McCoy,then R[x;α]/(xn)is left linearly McCoy. The converse holds if α is an automorphism;

(3)If α2=α and R is left linearly McCoy,then R[x;α]/(xn)is left linearly McCoy.

Proof. Let

and

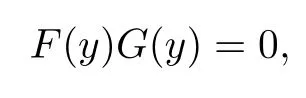
where

Write

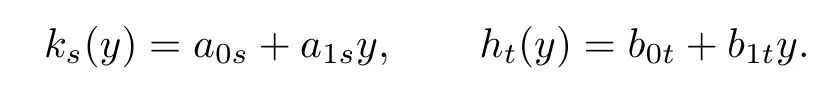
Then

(1)Suppose that k0(y)/=0 and hk(y)/=0 with k minimal.Then(∗)implies that

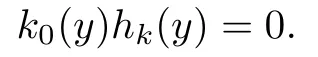
So there exists r1∈R{0}such that

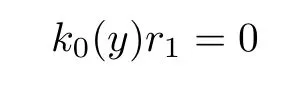
implies

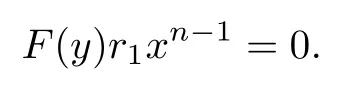
If

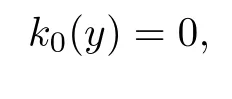
then

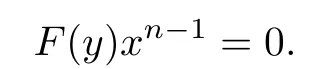
Therefore R[x;α]/(xn)is right linearly McCoy.

Conversely,let f(y)and g(y)be linear polynomials of R[y]{0}(⊆R[x;α]/(xn)[y])with f(y)g(y)=0.Since R[x;α]/(xn)is right linearly McCoy,there existssuch that

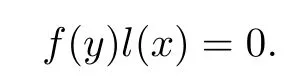
Let ck0be any nonzero coefficient of l(x).Then

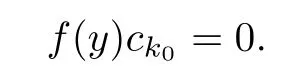
Thus,R is a right linearly McCoy ring.

(2)If h0(y)=0,then

Next suppose that h0(y)/=0 and kl(y)/=0 with l minimal.Thus

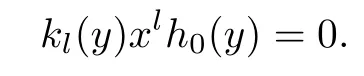
It follows that

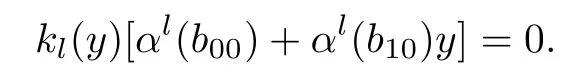
Since α is monic,we have

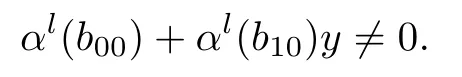
Because R is left linearly McCoy,there exists r2∈R{0}such that

So

It implies that

and

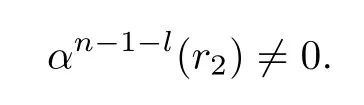
Put

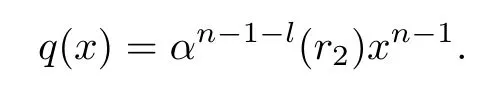
Then

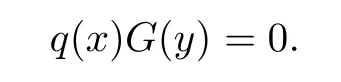
Hence R[x;α]/(xn)is left linearly McCoy.

Next suppose that α is an automorphism.Let f(y)and g(y)be the same as the“if”part in(1).By a similar proof,we can obtain that there existssuch that

Because α is an automorphism,there exists a nonzero elementR such that

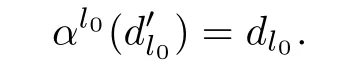
So

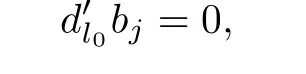
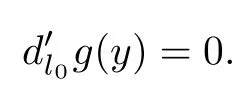
whence

Thus R is a left linearly McCoy ring.

(3)The proof of(2)only needs minor modi fi cations to apply here.

Remark 2.2By Example 2.2 in[7],we conclude that for a left linearly McCoy ring R,“R[x;α]/(xn)is left linearly McCoy”in Proposition 2.3(2)cannot imply that α is monic or epic.

3 α-skew Linearly McCoy Rings

In this section we introduce and explore α-skew linearly McCoy rings.The properties of α-skew linearly McCoy rings are studied.

De fi nition 3.1Let α be an endomorphism of a ring R.R is called α-skew linearly McCoy if whenever linearly polynomials p(x)=a0+a1x and q(x)=b0+b1x are nonzero in R[x;α] with p(x)q(x)=0,then there exists r∈R{0}such that aiαi(r)=0 for i=0,1.

Clearly,a ring R is right linearly McCoy if and only if it is an IR-skew linearly McCoy ring,where IRis the identity endomorphism of R.But the McCoy rings are not always α-skew linearly McCoy for some ring endomorphism α by the following example.

Example 3.1Let

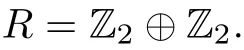
Then R is an McCoy ring.Let α:R→R be de fi ned by

For

we have

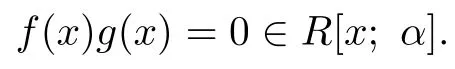
Write r=(a,b)∈R.If f(x)r=0,then

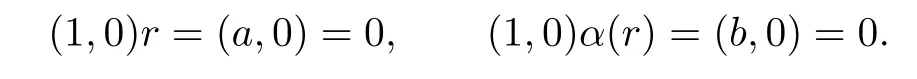
So r=0.Hence R is not an α-skew linearly McCoy ring.

Based on Example 3.1,it is natural to ask whether α-skew linearly McCoy rings are right linearly McCoy.The following example eliminates the possibility.

Example 3.2Let Z be the ring of integers.Consider the ring

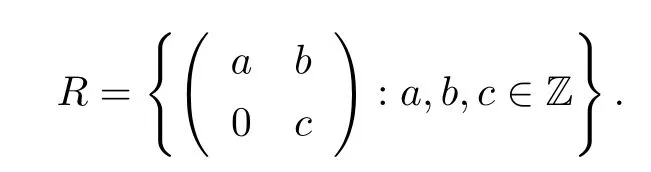
Then R is not right linearly McCoy by Proposition 10.2 of[4].Let α :R → R be an endomorphism de fi ned by

Set

with

where

Clearly,if either B0or B1is zero,then

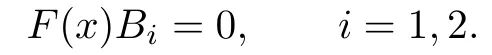
So we may assume Bi

/=0 for each i.Suppose tha tWrite

Then

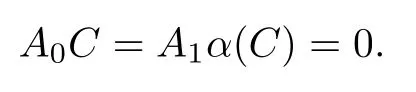
Then we have

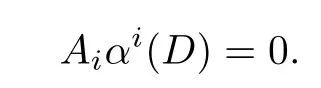
Thus R is an α-skew linearly McCoy ring.

Furthermore,we have the following result.

Proposition 3.1Let R[x]be the polynomial ring over any ring R,and an endomorphismbe de fi ned as α(f(x))=f(0)for any f(x)∈R[x].Then R[x]is an α-skew linearly McCoy ring.

Proof. Let

with

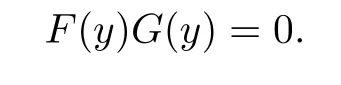
Since G(y)/=0,take h(x)=gk(x)x for the minimal index k such that gk(x)/=0.Note that

It follows that

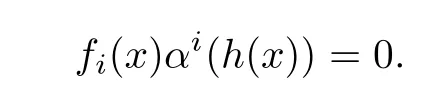
Therefore R[x]is an α-skew linearly McCoy ring.Let αibe an endomorphism of a rQing RiforQ each i∈Γ.Then for the ring direct productthe endomorphisms de fi ned by

PropQosition 3.2Let αibe an endomorphism of a ring Rifor i∈Γ.Then the ringskew linearly McCoy if and only if each Riis αi-skew linearly McCoy.

Proof. Let

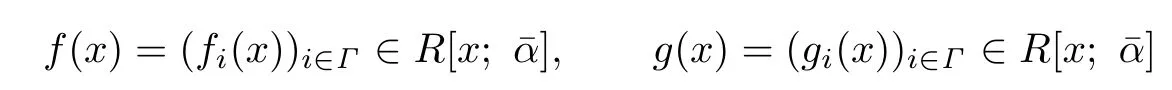
be nonzero linearly polynomials with

Suppose that each ring Riis αi-skew linearly McCoy.Since g(x)/=0,there exists some index i0∈Γ with gi0(x)/=0.We have

Then there exists some nonzero ri0∈Ri0such that

by the αi0-skew linearly McCoy property. Let r be the sequence with ri0in the i0-th coordinate,and zeros elsewhere.Then

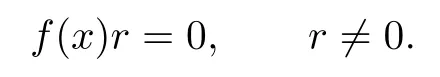
Hence R is an¯α-skew linearly McCoy ring.

Conversely,for any fi xed i0∈Γ,assume that p(x)q(x)=0 with linearly polynomialsLet

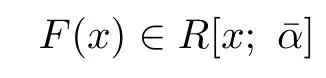
with p(x)in the i0-th coordinate and 1 elsewhere,and G(x)∈R[x;¯α]with q(x)in the i0-th coordinate and 0 elsewhere.So

By hypothesis,there exists rR{0}such that

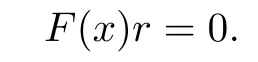
In particular,we have

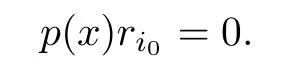
Clearly,

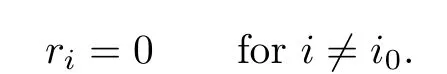
But r/=0 implies ri0

/=0.Therefore,Ri0is an αi0-skew linearly McCoy ring.By the arbitrariness of i0∈Γ,we are done.

For a ring R,we consider the ring

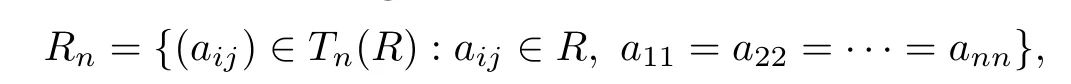
where Tn(R)is the upper triangular matrix ring over R and n is a positive integer.An endomorphism α of a ring R is extended to the endomorphism α¯:Rn→Rnde fi ned by

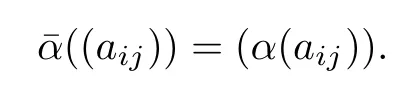
We have the following result.

Proposition 3.3Let α be an endomorphism of a ring R.Then R is α-skew linearly McCoy if and only if Rnis¯α-skew linearly McCoy.

Proof. “⇒”. For any H(x)∈Rn[x;],H(x)can be written as the form of a matrix.Let be the(i,j)-entry of H(x).Then hij(x)is a polynomial of R[x;α].

Suppose that F(x),G(x)are nonzero linear polynomials of Rn[x;α¯]with

We show that there exists A∈Rn{0}such that

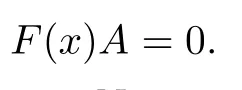
We use eijto denote the usual matrix unit.Now we proceed with the following cases.

Case 1.If f11(x)/=0,g11(x)/=0,then

where

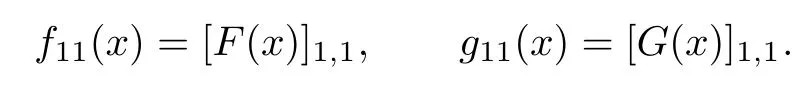
Since R is α-skew linearly McCoy,there exists s∈R{0}such that

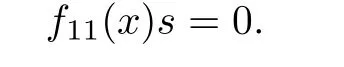
Put

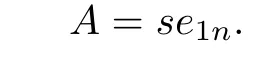
Then

Case 2.If f11(x)/=0,g11(x)=0,then there exists gkl(x)/=0(since G(x)/=0)satisfying

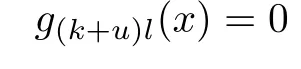
for some k,l and 1≤u≤n−k.So

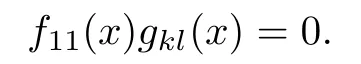
As in Case 1,there exists A∈Rn{0}with F(x)A=0.

Case 3.If f11(x)=0,then

for any nonzero s∈R.Set

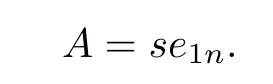
It is obvious that

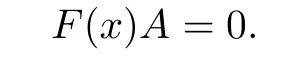
Therefore,Rnis an-skew linearly McCoy ring.

“⇐”.Let f(x)g(x)=0 with f(x)and g(x)being linear polynomials of R[x;α]{0}. Let

with Enbeing the n×n identity matrix.Then

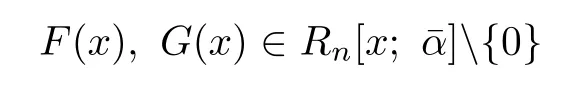
and

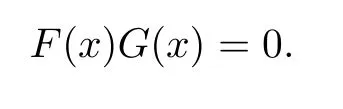
Since Rnis¯α-skew linearly McCoy,there exists a nonzero A∈Rnsuch that

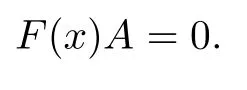
Obviously,

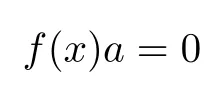
for some a∈R{0}.Thus,R is α-skew linearly McCoy.

Let Mn(R)(resp.,Tn(R))be the n×n matrix ring(resp.,n×n upper triangular matrix ring)over R.Similar to that of in Proposition 3.3,we can de fi ne the extended endomorphism ¯α of Mn(R)(resp.,Tn(R)).We have the following assertion.

Proposition 3.4If α is a monomorphism of a ring R and α(1)=1,then Mn(R)(resp., Tn(R))is not¯α-skew linearly McCoy for n≥2.

Proof. Denote the usual matrix unit by eij.Let

Then

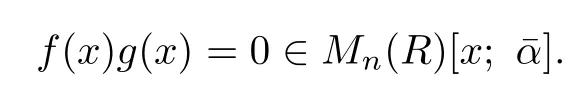
If there exists A=(aij)∈Mn(R)satisfying

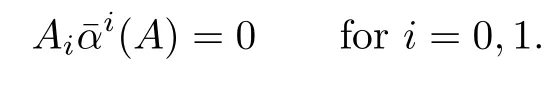
Then A0A=0 implies that

And it follows that α(anj)=0 by A1¯α(A)=0.Since α is monomorphic,we have

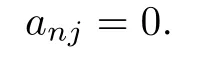
So

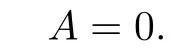
Noting that f(x),g(x)∈Tn(R)[x;¯α],by the same proof we can also show that Tn(R)is not¯α-skew linearly McCoy.

Corollary 3.1([4],Proposition 10.2) Let R be a ring,then Mn(R)(resp.,Tn(R))is not right linearly McCoy for n≥2.

We conclude that α being monic in Proposition 3.4 is not super fl uous by the following example.

Example 3.3Let T=R[x]be the polynomial ring over any ring R.An endomorphismis de fi ned as

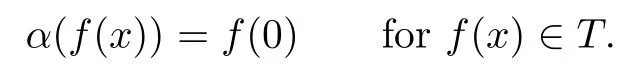
Then T is α-skew linearly McCoy by Proposition 3.1,but α is not monic.Let

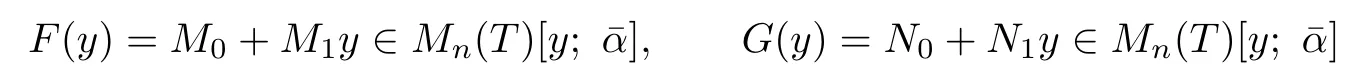
with

where

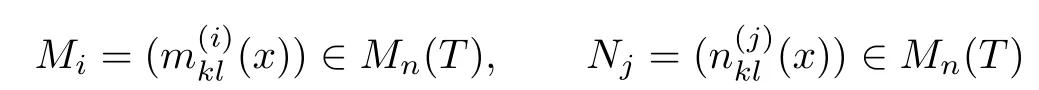
for i,j=0,1 and 1≤k,l≤n.We assume that N is nonzero.Let

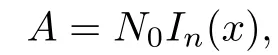
where In(x)=xEnand Enis the n×n identity matrix.Then

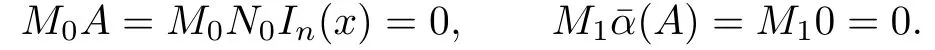
Hence Mn(T)isα¯-skew linearly McCoy.By the same discussion we can prove that Tn(T) is alsoα¯-skew linearly McCoy.

If α is an endomorphism of a ring R,then a map of the polynomial ringde fi ned byis also denoted by α.Clearly,this map extends α.

Remark 3.1There exists a linearly McCoy ring R in Example 2.2.1 of[10],which satis fi es that the polynomial ring R[x]is not IR-skew linearly McCoy.

For an ideal I of a ring R,if α(I)⊆I then¯α:R/I→R/I de fi ned by

is an endomorphism of the factor ring R/I.

Theorem 3.1Let α be an endomorphism of a ring R and n≥2.If R is α-skew linearly McCoy and α(1)=1,thenis an¯α-skew linearly McCoy ring.

Proof. Denote¯x in R[x]/(xn)by u.Then

where u commutes with elements in R and un=0.

Let

where

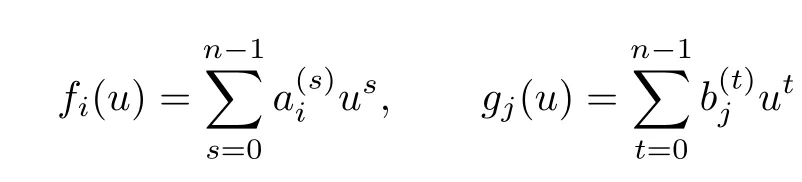
for i,j=0,1.Since α(1)=1,one has

Suppose that F(y)G(y)=0∈R[u][y;¯α].Then

In particular,we have

with index k minimal(since G(y)/=0,k exists)such that

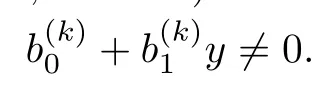
Case 1.Suppose that

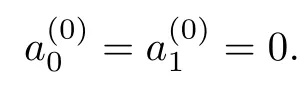
Let

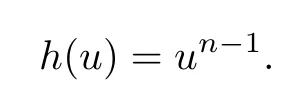
Then

since¯α(u)=u and un=0.

Case 2.Assume that

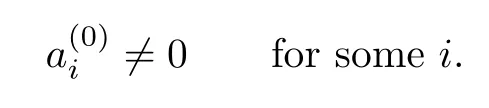
Since R is α-skew linearly McCoy,(∗∗)implies that there exists c∈R{0}such that

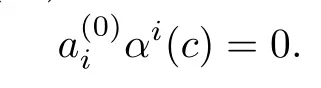
Write

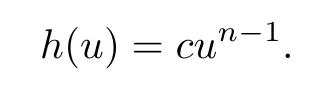
Then

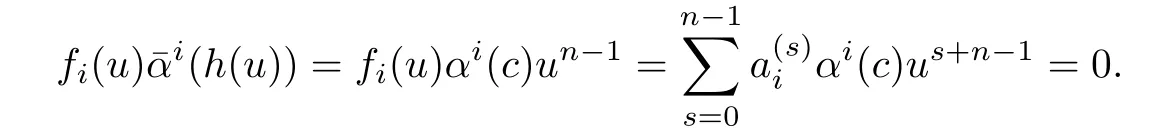
Therefore,R[x]/(xn)is an¯α-skew linearly McCoy ring.

Corollary 3.2A ring R is right linearly McCoy if and only if the ring R[x]/(xn)is right linearly McCoy with(xn)being the ideal generated by xnand n≥2.

[1]McCoy,N.H.,Remarks on divisors of zero,Amer.Math.Monthly,49(1942),286–295.

[2]Rege,M.B.and Chhawchharia,S.,Armendariz rings,Proc.Japan Acad.Ser.A,Math.Sci., 73(1997),14–17.

[3]Nielsen,P.P.,Semi-commutativity and the McCoy condition,J.Algebra,298(2006),134–141.

[4]Camillo,V.and Nielsen,P.P.,McCoy rings and zero-divisors,J.Pure Appl.Algebra, 212(2008),599–615.

[5]Hong,C.Y.,Kim,N.K.and Kwak,T.K.,On skew Armendariz rings,Comm.Algebra, 31(2003),103–122.

[6]Lei,Z.,Researches on McCoy rings,Master’s thesis,Southeast University,Nanjing,2008.

[7]Ying,Z.L.,Chen,J.L.and Lei,Z.,Extensions of McCoy rings,Northeast.Math.J.,24(2008), 85–94.

[8]Huh,C.,Lee,Y.and Smoktunowicz,A.,Armendariz rings and semicommutative rings,Comm. Algebra,30(2002),751–761.

[9]Kim,N.K.and Lee,Y.,Armendariz rings and reduced rings,J.Algebra,223(2000),477–488.

[10]Cui,J.,Researches on linearly McCoy rings,Master’s thesis,Southeast University,Nanjing, 2009.

16S30,16S99

A

1674-5647(2010)02-0159-17

date:April 20,2009.

TheNSF (10871042,10971024)ofChinaand theSpecializedResearch Fund (200802860024)for the Doctoral Program of Higher Education.