基于岩石物理模型的最优化AVO三参数同步反演方法*
张世鑫印兴耀孔国英张繁昌
(1.中国石油大学(华东)地球资源与信息学院; 2.中海油研究总院)
基于岩石物理模型的最优化AVO三参数同步反演方法*
张世鑫1印兴耀1孔国英2张繁昌1
(1.中国石油大学(华东)地球资源与信息学院; 2.中海油研究总院)
由于反射系数线性近似公式受到小角度入射和界面弹性参数差异小的基本假设的限制,常规AVO反演在大角度入射和界面弹性参数差异大的情况下存在严重不确定性。提出了基于岩石物理模型的最优化AVO三参数同步反演方法,该方法将研究工区的特定岩石物理条件作为先验软约束融合到反射系数近似公式中,以最优反射系数近似为基础实现了最终的三参数同步反演。从应用效果看,基于岩石物理模型的最优化三参数同步反演具有更强的工区适用性,减小了常规反射系数近似公式的基本假设对反演结果的影响,而且正交基函数提高了AVO反演的可靠性。
最优化近似公式 岩石物理模型 AVO 三参数同步反演 反射系数
AVO分析的理论基础是Zoeppritz方程,但由于Zoeppritz方程的复杂性与物理意义的不直观性,在实际应用中普遍使用更为简便的反射系数线性近似公式[1](如Aki和Richard近似、Shuey近似等)。但是,常规线性近似公式都是建立在一系列假设基础之上的,主要假设有2点:一是相邻地层介质的弹性参数差异较小;二是入射角小于临界角。随着油气勘探寻找的目的储层越来越复杂,很多砂岩、碳酸盐岩等高速层界面两侧介质的弹性参数差异较大,以及对大角度地震资料的重视,只适用于小角度入射的常规线性近似公式必然会影响参数估计的精度和有效性。为解决这些问题,Causse等人[2-3]提出了基于岩石物理模型的最优化近似公式,可以较好地克服常规反射系数近似的局限性,进行储层类型划分与常规AVO属性提取;Varela等人[4]提出了基于最优化近似公式的最优系数,可以反演裂缝密度。笔者则提出以岩石物理模型的最优化反射系数近似公式为基础进行常规弹性参数同步反演的方法,经过理论模型分析与实际应用,表明该方法是有效、可靠的。
1 反演方法原理
1.1 最优化反射系数近似公式
最优化近似公式将反射系数用一个线性通式表示[2-3],即
式(1)中:fi(θ)和Ci分别是最优基函数和系数。
若已知地层的岩性信息,假设该岩性地层的物性参数服从某一合理的概率分布,根据该分布构建N个属于该岩性地层的物性参数模型(主要包括纵横波速度和密度);若假设有M个离散的入射角度,利用Zoeppritz方程可以得到这 N个参考模型的反射系数曲线分布(如图1,在此假设只有含水砂岩与泥岩以及含气砂岩与泥岩这2种类型的岩性分界面,为方便说明方法的优越性,2种界面均属于第一类AVO情况,实际情况要比这复杂得多),构建一个M×N维的反射系数矩阵R(注意建立模型时M >N)。
对反射系数矩阵R进行奇异值分解运算,即

式(2)中:矩阵V,D和F的维数分别为N×N、N× N和M×N。根据奇异值分解的性质可知,V为正交矩阵,D为对角阵,F的列是标准正交的。对于给定的模型,相关AVO曲线的主要特征信息随基函数次序的增加而降低,并且考虑到奇异值递减速度很快,忽略高次项基函数对近似精度影响很小,本文研究主要针对三项基函数近似。
经奇异值分解得到基函数矩阵 F后,选择合适项数的最优基函数,结合对应界面的准确反射系数,采用最小二乘法计算得到最优系数 Ci,即
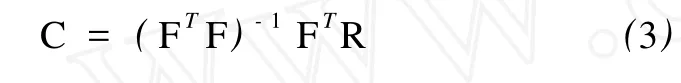
1.2 岩石物理模型的建立
基于最优化反射系数进行叠前AVO反演提取属性参数时,首先建立工区内各种岩相的纵横波速度与密度随深度的变化趋势,以此作为岩相模型的平均值;然后假设取值服从某一合理的概率分布,构建各类岩相的岩石物理模型;最后结合研究工区的地质规律,对岩相模型进行相应组合后计算模型界面的准确反射系数。
本次研究考虑到实际工区埋深较浅,采用Avseth等人提出的趋势模型的建立方法[5-6],主要步骤如下:
(1)建立孔隙度随深度的变化趋势
Ramm和Bjørlykke提出了一种砂岩孔隙度(φ)与深度(z)并依赖粘土的回归模型,即
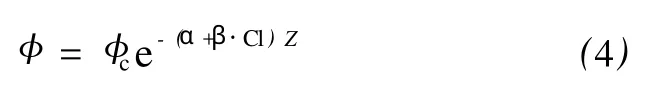
式(4)中:φc表示临界(即沉淀)孔隙度;α和β是回归系数,分别代表纯砂岩骨架颗粒稳定因子(Cl=0)和描述随粘土含量增加的敏感性因子;Cl表示泥质因子,定义为相对于稳定骨架颗粒总含量的总粘土含量。使用合适的地面临界孔隙度值(砂岩一般为0.40~0.45,泥岩为0.6~0.8)和任意埋藏深度反演的密度测井值校正局部孔隙度-深度趋势。
(2)根据孔隙度随深度的变化趋势直接得到密度变化趋势,即
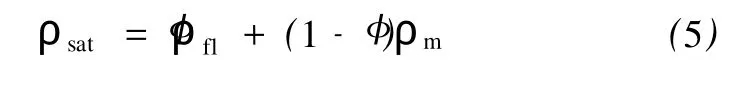
式(5)中:ρsat是饱和岩石密度;ρfl是流体密度;ρm是矿物密度;φ是孔隙度。对于干岩石来说,流体密度等于零。
(3)根据Hertz-Mindlin接触理论与Gassmann理论计算得到纵横波速度随深度的变化趋势
首先根据 Hertz-Mindlin理论计算未固结沉积物的弹性模量(根据该理论可知,弹性模量是孔隙度和压力的函数),得到弹性模量随深度的变化趋势,进而可以计算纵横波速度随深度的变化趋势。
Hertz-Mindlin接触理论中定义干岩样的弹性模量通过下式计算
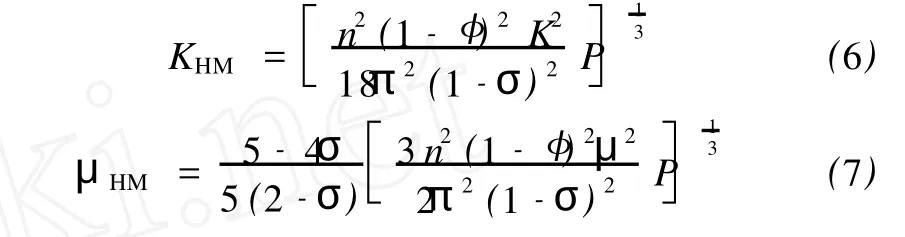
式(6)、(7)中:KHM和μHM分别表示孔隙度为φ的体积模量和剪切模量;P表示压差,对于不同深度的有效压力,P=g∫z0(ρb-ρl)dz,g是重力常数,ρb和ρl分别是给定深度时的岩石固体密度和流体密度;K、μ和σ分别表示固体相的体积模量、剪切模量和泊松比;n表示配位数(每个颗粒的接触颗粒数目),配位数与孔隙度之间的关系可近似为 n=20-34φ+ 14φ2。饱和岩样的弹性模量 Ksat和μsat可以用 Gassmann方程计算得到。
得到 Ksat,μsat和ρsat之后,便可以计算饱和岩样的纵波速度Vp和横波速度Vs,即
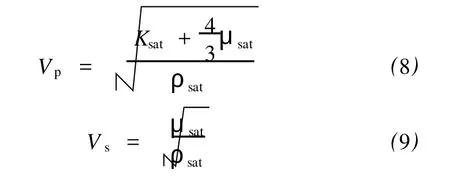
1.3 弹性参数优化
最优系数和常规近似系数之间存在一定的关系,Causse等人[2-3]研究了Aki-Richard近似公式中弹性参数的优化问题,给出了如下公式

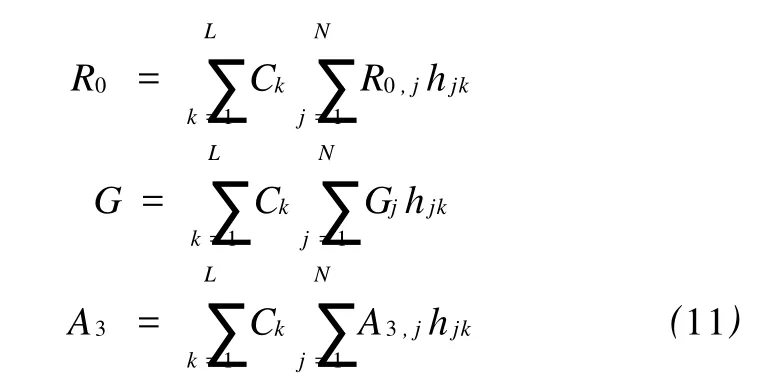
式(11)中:L为所选基函数个数;N为所建模型的个数;hjk表示矩阵 H=W-1=VTD-1的第 j行第k列元素。

1.4 反演方程的建立
以矩阵形式表示最优化反射系数为

式(12)中:R是反射系数矩阵;F是最优基函数矩阵;C是最优系数矩阵。
如果考虑褶积模型,地震记录表示为子波与反射系数的褶积,式(12)用矩阵形式表示为
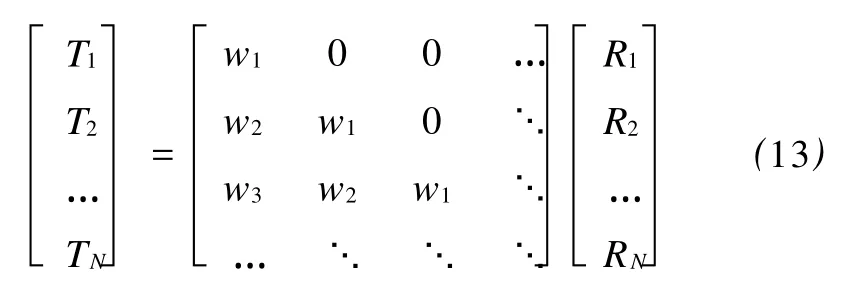
式(13)中:Ti表示地震道的第i个采样点;wj表示提取地震子波的第j个采样点;Ri表示第i个采样点的反射系数。综合式(13)可以得到如下公式:

由于最优系数Ci(i=1,2,3)之间是正交的,所以在求解反演系数时不必计算协方差矩阵去相关,直接采用最小二乘法计算 Ci(i=1,2,3)。得到 Ci(i=1, 2,3)之后,利用公式(11)可以进一步优化得到弹性参数相对变化量(Rp=ΔVp/Vp,Rs=ΔVs/Vs,Rd= Δ ρ/ρ)。
根据关系
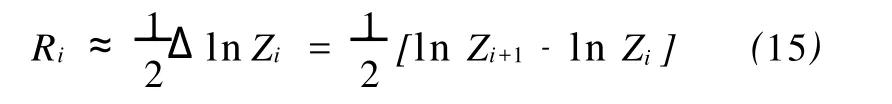
式(15)中:Ri表示第i层和第i+1层之间界面的反射系数。如果我们考虑 N个采样点,则式(15)以矩阵形式表示为

式(16)中:Li=lnZi。
分别针对 Rp、Rs和 Rd求解矩阵(16),可以最终得到参数Vp、Vs和ρ。
2 模型试算
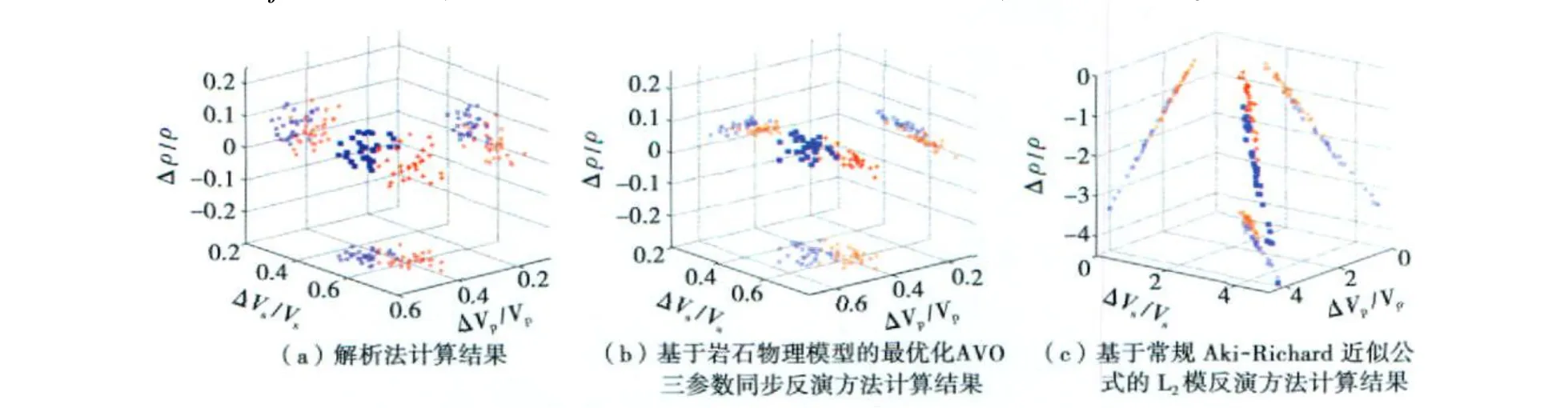
图2 模型数据提取的弹性参数相对变化量的三维交会显示
以图1所示含水砂岩与含气砂岩(第一类AVO)为模型进行相应弹性参数提取的试算。分别采用解析法、基于岩石物理模型的最优化AVO三参数同步反演方法(即本文方法)和基于常规Aki-Richard近似公式的L2模反演方法对该模型进行弹性参数相对变化量(ΔVp/Vp,ΔVs/Vs,Δ ρ/ρ)的提取并计算常规属性;分别对计算的3个属性进行三维交会显示,如图2所示。
在图2中,解析解表示模型弹性参数变化量的准确分布(图2a);将图2b、图2c与图2a比较可知,在满足一定误差条件下,基于岩石物理模型的最优化AVO三参数同步反演方法提取的3个弹性参数相对变化量与准确值基本吻合(弹性参数相对变化量是基于常规AVO属性与弹性参数之间的近似关系间接计算得到的,不可避免的会引入一定误差),但基于常规Aki-Richard近似公式的L2模反演方法计算的弹性参数相对变化量与解析解之间的误差非常大。这说明,基于常规的AVO近似公式的反演方法无法满足弹性参数差异大的界面以及需要大角度信息参与情况下的弹性参数的可靠反演,而本文提出的基于岩石物理模型的最优化AVO三参数同步反演方法可以较好地弥补这一不足,应用该反演方法所得到的储层的弹性参数能够有效地表征储层信息。
3 实际应用
将该方法应用到某勘探区块。反演之前首先要对地震数据和测井数据进行预处理[7],对地震记录采用去多次波、几何扩散校正、地表一致性反褶积、振幅补偿、保幅叠前偏移等技术进行处理之后得到叠前道集。
反演中首先根据测井和岩性解释资料将研究工区岩相划分为4类模型(图3),建立各种岩相随深度变化的岩石物理模型;然后两两组合建立相应的界面,对应得到准确的反射系数矩阵;对反射系数矩阵进行奇异值分解,得到不同深度最优反射系数的基函数,最终反演得到纵波速度、横波速度和密度等3个弹性参数体。
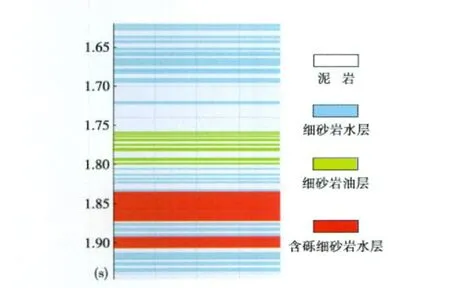
图3 根据测井资料划分的研究工区4种岩相类型
由于受到地球物理模型精度的限制,只能在较小的时窗内进行弹性参数反演,本次实际应用选择的时间段是1.6~2.0s,该时间段内有2个含油目的层段。图4是其中一条测线的反演结果,图中测井曲线是电阻率曲线,可以看到,油层处纵波速度降低,密度降低,相应的横波速度并没有较大变化。通过岩石物理分析可知,上述特征符合研究工区的储层特征,并且反演的井旁道与测井曲线在误差允许的范围内匹配较好,表明了本文提出的弹性参数反演方法的有效性。
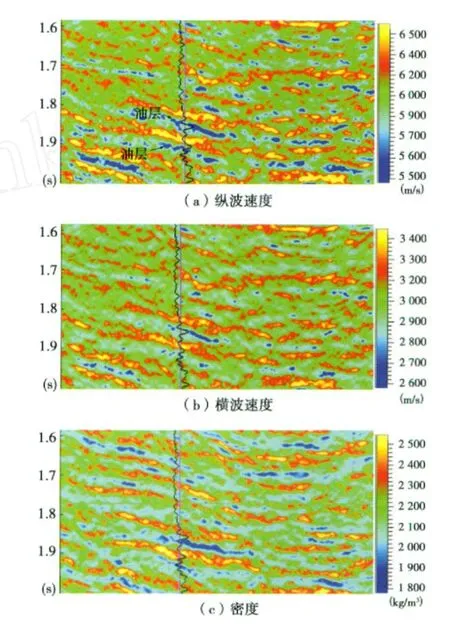
图4 研究工区弹性参数反演剖面
4 结论
与常规AVO弹性参数反演方法相比,本文提出的基于岩石物理模型的最优化AVO三参数同步反演方法克服了常规反射系数近似公式存在的缺陷,适用于近临界角入射以及界面物性差异大的情况。由于本文方法中基函数是正交的,所以不同系数所包含的噪声不相关,而且有着相同的幅度和方差(在近似公式中选择的系数少,相当于利用低通滤波器进行去噪处理),因此应用本文方法估算的参数的抗噪能力更强。另外,由于岩石物理模型作为先验信息在公式推导中起到了软约束的作用,因此所得到的最优反射系数近似公式具有工区适定性,提高了AVO定性和定量解释的精确性,最终得到了稳定可靠的反演结果。
需要指出的是,岩石物理模型建立的正确与否对本文方法起到至关重要的作用,而且影响因素的多样性和复杂性制约了岩石物理模型建立的可靠性,因此在研究中必须结合研究工区特征灵活地选择最为合适的模型建立方法。
[1] TARANTALA A.Inversion problem theory and methods for model parameter estimation[M].Philadelphia:Society for Industry and Applied Mathematics,2004.
[2] CAUSSE E,RIEDE M,WIJ INGAARDEN A J,et al.Amplitude analysis with an optimal model-based linear AVO approximation:PartⅠ—Theory[J].Geophysics,2007,72:59-69.
[3] CAUSSE E,RIEDE M,WIJ INGAARDEN A J,et al.Amplitude analysis with an optimal model-based linear AVO approximation:PartⅡ—Field data example[J].Geophysics,2007, 72:71-79.
[4] VARELA I,SONJA M,LI Xiangyang.Fracture density inversion from a physical geological model using azimuthal AVO with optimal basis function:79th annual international meeting [C].SEG,Expanded Abstracts,2009:2075-2079.
[5] AVSETH P,FLESCHE H,WIJ INGAARDEN A J.AVO classification of lithology and pore fluids constrained by rock physics depth trends[J].The Leading Edge,2003,22:1004-1011.
[6] AVSETH P,MU KERJ I T,MAVKO G,Quantitative seismic interpretation[M].Cambridge:Cambridge Univ.Press,2005.
[7] SHERIFF R E.Factors affecting seismic amplitudes[J].Geophys Prospect,1975,23:125-138.收稿日期:2010-02-03 改回日期:2010-05-24
(编辑:周雯雯)
Abstract:Because the reflection coefficient approximation is limited by the basic assumptions of a low-angle incidence and small differentiation in interfacialelasticity coefficient,any conventional AVO inversion will be seriously uncertain with a high-angle incidence and large differentiation in interfacial elasticity coefficient.Therefore,an optimal simultaneous inversion method for AVO with three parameters has been developeds on a petrophysics-model basis,in which the special petrophysical conditions in a study area can be integrated into the reflection coefficient approximation as a prior soft constraint,and a simultaneous inversion with three parameters is implemented on a basis of the optimal reflection coefficient approximation. The application results have shown that this AVO inversion is higher in adaptability for study areas, and can decreasse the impacts of the basic assumptions for the conventional reflection coefficient approximation on the inversion result,and that the orthogonal basic functions can make the AVO inversion more reliable.
Key words:optimal approximation;petrophysics model;AVO;simultaneous inversion with three parameters;reflection coefficient
An optimal simultaneous inversion method for AVO with three parameters on a petrophysics-model basis
Zhang Shixin1Yin Xingyao1Kong Guoying2Zhang Fanchang1
(1.College of Geo-Resources and Inf ormation,China University ofPetroleum(East China),Shandong,266555;
2.CNOOC Research Institute,Beijing,100027)
*国家重大专项(2008ZX05030-04-001-001)和中国石油大学优秀博士学位论文培育资助项目(z10-01)部分研究成果。
张世鑫,男,中国石油大学(华东)在读博士研究生,主要从事地震反演、储层预测方面的研究。E-mail:zsxvegata@126.com。

