雾对“日盲”紫外光传输的影响分析
马冬冬 刘宗福 金 虎/中国人民解放军92785部队
0 引言
人们当前所掌握的通信手段主要有无线电通信、微波通信、有线通信和光纤通信等几种,这些通信手段在军事通信联络中起到了重要的作用,同时也存在一些不足。而光无线通信结合了光纤通信与微波通信的优点,既具有通信容量大,又不需要铺设光纤。它以光束作为信息载体,是不需要任何有线传输媒介的通信方式,可用于空间及地面通信,其传输特点是光束以直线传播。作为对微波通信的革命,光无线通信系统得到人们的普遍重视,紫外光通信是一种新的无线光通信技术,它兼光无线通信的优点之外还具有非视线传输的能力,因而得到了研究人员的青睐。但是天气因素对无线激光通信具有不同程度的影响。雾是一种常见的自然天气现象,由于雾滴的散射和吸收作用,会使光的传输产生衰减,这就限制了光通信的传输距离。
1 紫外光散射的传输特性
紫外光散射通信是通过发射“日盲区”波长( 200~280 nm)的紫外光来携带通信信息, 以大气为传输媒介, 利用紫外光在大气中传输的散射特性来进行自由空间近程通信的一种光通信手段。作为一种新兴的通信手段, 紫外光散射通信技术具有其独特的特点和要求。
紫外光在大气中传播时,具有两个典型特征[1]。
(1)指数规律的能量衰减受到大气中所含分子、悬浮颗粒等的吸收和散射,信号能量按指数规律衰减快,大气瑞利散射造成的光能损失是红外线的1000倍以上。因此,发射的“日盲区”信号可以探测的距离被限制在几千米之内,在一定区域外根本无法进行截获、侦听。
(2)极强的散射特性。紫外光波长较短,在传输过程中受到大气的散射作用很强,可以有效地实现“非直视”(NLOS)通信。紫外辐射的散射特性是通信系统非视线工作方式的基础,这种工作方式克服了其他自由空间光通信系统必须工作在视线方式的弱点。
2 Mie(米氏)理论简介
1908年,米氏应用电磁场理论,求解均匀介质中任意尺寸、任意成分的均匀球体对入射单色平面波的散射,得到了严格的解析解[2]。Mie散射解不仅适用于单个球体的散射,而且适用于多个球体的散射问题。只要多个球体具有相同直径和成分且无规则分布,彼此分开的距离比入射波长大得多即可。这时不同球体的散射电磁场无确定相位关系,总散射能量是各个球体散射能量的总和。因此,Mie理论对研究光(电磁波)在大气、水以及云、雨、雾和气溶胶中的传播方面有着广泛的应用。根据Mie理论,消光系数、散射系数和吸收系数定义如下[3]:
散射系数(散射效率因子):

衰减系数(衰减效率因子):
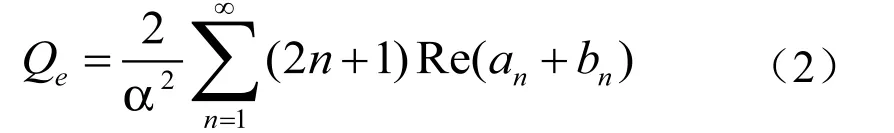
式中 α 为颗粒尺寸参数 (α = π D / λ );
an、bn称为Mie系数,可由下式计算得到:
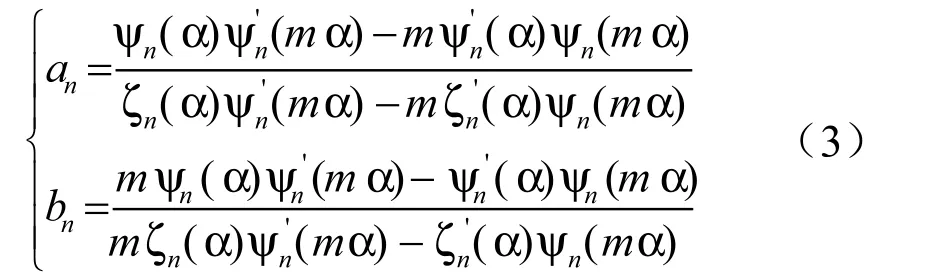
其中:m=nr- ini为粒子相对周围介质折射率,当虚部不为零时,表示粒子有吸收。

3 雾的尺寸分布
研究云雾粒子散射常用的模型有,1968年Chu(朱氏)和Hogg(霍格)用修正Γ函数稳定状态雾滴分布[3],这种模型的缺点是参数需要实验确定。另一种常用且适用性最大的是广义gamma(伽马 )分布如 n(r)= arαexp(-brβ),这种分布的优点是用单一的能见度即可确定雾滴的尺寸分布;在这种模型下云雾尺寸分布参数与宏观物理量之间的关系更为简洁,被广泛采用的另一种较为简单云雾滴谱模型为,α=2,β=1时的gamma雾滴尺寸分布模型(Khragian-Mazin分布模型),即:

下文将依此模型为基础,导出云雾滴谱分布与能见度和含水量间的关系。同时由于雾的含水量和能见度的经验关系[3],能见度的单位取km,所以得到:

将 a和b代入Khragian-Mazin分布模型,同时由于雾滴尺寸通常用微米(μm)表示,得到雾滴粒子半径以微米表示的雾滴尺寸分布:
平流雾:

辐射雾:

4 紫外光传输的衰减
当强度为I0的光通过距离为 的介质,根据Bougure定律[3],其强度为可表示为:

其中, 为单次散射近似时的衰减系数:

Adarsh Deepak[4][5]等人对多次散射和前向散射的问题进行了研究,证明在多次散射影响下,光束的前向几度范围内存在一个比较大的峰值,这种前向峰值效应使得光衰减大大降低。Adarsh Deepak和O.H.Vaughan[6]提出一个前向散射修正系数 的近似公式:

其中,α为尺度参数,θ为散射角,J0(αθ)和J1(αθ)为零阶和一阶第一类贝塞尔函数。同时,他们认为在 r > λ 和 θ ≤ 1.5°时,与精确公式相比误差小于2%。因此,本文将其引入到雾激光传输衰减上,对单次散射公式进行再次修正,修正后可考虑多次散射的影响,以便于浓雾的计算。
修正后的衰减效率因子:
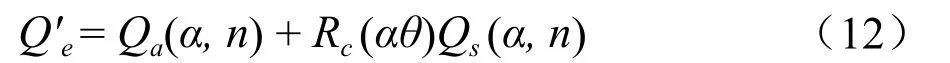
对于紫外波段,由水复折射可以看出[7],粒子对光的吸收相对于散射可以完全忽略。这样

由于衰减率通常用分贝表示,定义如下:

将(9)式带入(13)式并取z=1 km 得:

再结合(10)(11)(14)式得到修正后的衰减计算公式:

5 分析及结论
下文是应用新的衰减公式,对波长为200 nm、225 nm、250 nm和275 nm的“日盲”紫外光在平流雾、辐射雾中衰减进行计算与仿真(所对应的水复折射率分别为[7]:m = 1.396-i1.1×10-7、m = 1.373- i4.9×10-8、m = 1.362- i3.35×10-8和 m = 1.354 - i2.35×10-8)。
图1为紫外光在平流雾中衰减随能见度的变化,通过该图可以很清楚地看到紫外线在“日盲区”衰减的差异很小,即使在能见度很低的雾中衰减,差异不超过20 dB/km,在能见度较高的雾中差异就更小,如在能见度500 m ~ 1000 m的轻雾中衰减的差异不到1 dB/km;在同一能见度下,长波长衰减大于短波长衰减。

图1 紫外光在平流雾中衰减随能见度的变化
图2为紫外光在辐射雾中衰减随能见度的变化,在图示能见度范围内,“日盲区”紫外光衰减差异同平流雾中差异相当。但是在同一能见度下,发现并不是长波长衰减大于短波长衰减,而是在250 nm处紫外光衰减最大。

图2 紫外光在辐射雾中衰减随能见度的变化
图3为紫外光在平流雾/辐射雾中衰减随波长的变化(空心是平流雾,实心是辐射雾),图中看出在整个“日盲区”,同一能见度下平流雾的衰减大于辐射雾的衰减,且能见度越低差异越大,最大可达50 dB/km,能见度越小差异越小,最小低至10 dB/km以下。
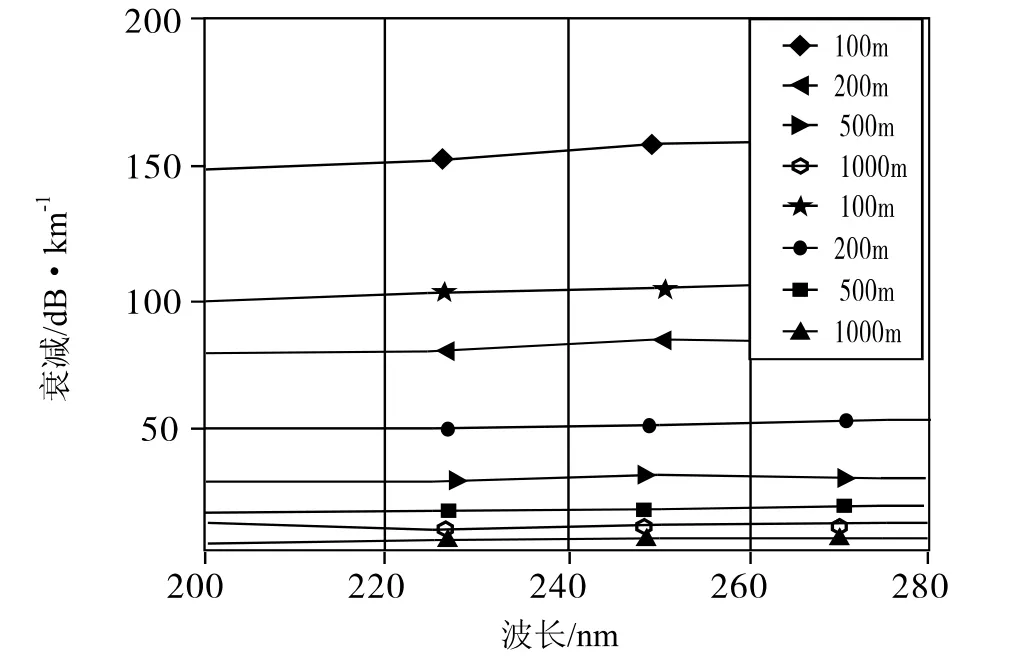
图3 紫外光在平流雾/辐射雾中衰减随波长的变化(空心是平流雾,实心是辐射雾)
[1]田培根, 王平, 王红霞. 紫外光散射通信接收技术研究[J].无线光通信,2006(9).
[2]石顺祥, 刘继芳, 孙艳玲.光的电磁理论-光的传播与控制[M].西安:西安电子科技大学出版社,2006 :121-132.
[3]宋正方. 应用大气光学基础[M].气象出版社, 1990: 17-60.
[4]Adarsh Deepak and Michael A Box. Forwardscattering corrections for optical extinction measurements in aerosol media. 1:Monodispersions[J]. APPLIEDOPTICS,1978,19 : 2901-2908.
[5]Adarsh Deepak and Michael A Box. Forwardscattering corrections for optical extinction measurements in aerosol media. 2:Polydispersions[J]. APPLIEDOPTICS,1978,19: 3169-3176.
[6]Adarsh Deepak and O H Vaughan. Extinction-sedimentation inversion technique for measuring size distribution of artificial fogs [J]. APPLIED OPTICS, 1978, 3 : 374-378.
[7]Hale,G.M.and Querry. Optical constants of water in the 200nm to 200um wavelength region[J].APPLIEDOPTICS, 1972, 12(3).555- 563.

