粒的运算及其分层结构研究

河南师范大学计算机与信息技术学院 王 川

粒的运算及其分层结构研究

河南师范大学计算机与信息技术学院 王 川

在传统粒计算理论的基础上，对粒的表示方法加以改进，从而使粒计算更具适用性，进而构建粒子空间，并将粒子空间投影到信息系统中得到其层次结构图，该分层结构能满足用户对数据局部分析或概化分析的兴趣点。

粒计算 分层结构 投影

一、引言

粒计算是一种新的基于问题概念空间划分的智能计算方法[1-6]。本文结合传统粒计算理论，考虑实际中数据分析兴趣习惯，在对粒的表示方法进行改进研究的基础上，进一步对新的粒结构进行分析并尝试应用，进而构建粒子空间，并将粒子空间投影到信息系统中得到粒的分层结构，从而满足用户对数据局部分析或概化分析的兴趣点，同时提高了数据分析的效率。

二、粒的表示方法及其运算

定义1 （公式的定义） 在信息系统S = (U, A, V, F )中，令a∈A，M⊆Va，(a, M)为一原子公式定义，以下简写为aM，定义如下的rough逻辑公式：

（1）aM是原子公式，原子公式是公式；若M = Va，则称aM为可缺省原子公式，不参与粒运算。

（2）如果A和B是原子公式，那么A∧B是公式，使用连接词∧进行有限次运算所组成的式子是公式。

定义2 （粒的定义） 函数h(a, M)表示所有在属性a(a∈A)上的值属于M(M⊆Va)的对象集，即h(a, M) = {x|a(x)∈M}，其中x∈U，则信息系统S = (U, A, V, F )中粒的定义为：Gr = ((a, M)，h(a, M))，其中(a, M)为粒Gr的语法，Gr被称为信息系统中的原子粒，若M = ∅，则h(a, M) = ∅，对应的原子粒Gr为空粒。设w是形如(a1, M1)∧(a2, M2)∧…∧ (an, Mn)的由原子公式使用逻辑连接词∧所得逻辑组合，

h(w)表示满足逻辑组合w的对象集合。Gr = (w, h(w))被称为满足逻辑组合w的组合粒。

定义1与定义2是在文献[3]基础上对公式和粒重新定义，其主要区别将原子公式(a, v)，a∈A，v∈Va，重新定义为(a, M)，a∈A，M⊆Va，意义在于扩大原子公式的适用范围。

定义 3 （粒分解运算） 一个组合粒Gr = (w, h(w))，其中w = (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，则Gr的分解Dec(Gr) = {Gr1, Gr2, …, Grn}，其中Gr1= ((a1, M1),h(a1, M1))，Gr2= ((a2, M2), h(a2, M2))，…，Grn= ((an, Mn), h(an, Mn))。

定义4 （交运算） 对于任意两个粒Gr1= (w1, h(w1))，Gr2= (w2, h(w2))，其中w1= (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，w2= (a1, K1)∧(a2, K2)∧…∧ (an, Kn)，则定义其交运算（∧）为：Gr1∧Gr2= (w3, h(w3))，其中w3= (a1, M1∧K1)∧(a2, M2∧K2)∧…∧ (an, Mn∧Kn)。

定义5 （并运算） 对于任意两个粒Gr1= (w1, h(w1))，Gr2= (w2, h(w2))，其中w1= (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，w2= (a1, K1)∧(a2, K2)∧…∧ (an, Kn)，则定义其并运算（∨）为：Gr1∨Gr2= (w3, h(w3))，其中w3= (a1, M1∨K1)∧(a2, M2∨K2)∧…∧ (an, Mn∨Kn)。

定理1对于任意两个组合粒Gri= (wi, h(wi))，Grj= (wj, h(wj))，其中wi= (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，wj= (a1, K1)∧(a2, K2)∧…∧ (an, Kn)，则满足Gri∧Grj= ∧(Dec(Gri)∨Dec(Grj))，Gri∨Grj= ∨(Dec(Gri)∨Dec(Grj))。

证明：由定义3可得，Dec(Gri) = {Gri1, Gri2, …, Grin}，其中Gri1= ((a1, M1), h(a1, M1))，Gri2= ((a2, M2), h(a2, M2))，…，Grin= ((an, Mn), h(an, Mn))；Dec(Grj) = {Grj1, Grj2, …, Grjn}，其中Grj1= ((a1, K1), h(a1, K1))，Grj2= ((a2, K2), h(a2, K2))，…，Grjn= ((an, Kn), h(an, Kn))。所以∧(Dec(Gr1)∨Dec(Gr2)) =∧{Gri1, Gri2, …, Grin, Grj1, Grj2, …, Grjn} = Gri1∧Grj1∧…∧Grin∧Grjn= ((a1, M1∧K1), h(a1, M1∧K1))∧…∧((an, Mn∧Kn), h(an, Mn∧Kn))，由定义4可得，Gri∧Grj= (wk, h(wk))，其中wk= (a1, M1∧K1)∧(a2, M2∧K2) ∧…∧(an, Mn∧Kn)，所以得Gri∧Grj= ∧(Dec(Gri)∨Dec(Grj))，同理可得Gri∨Grj=∨(Dec(Gri)∨Dec(Grj))。

性质1 对于任意两个粒Gr1= (w1, h(w1))，Gr2= (w2, h(w2))，Gr1= Gr2当且仅当Gr1∧Gr2= Gr1∨Gr2

定义6 对于任意两个粒Gr1= (w1, h(w1))，Gr2= (w2, h(w2))，若满足Gr1∨Gr2= Gr1且Gr1∧Gr2= Gr2，则称粒子Gr1是Gr2父粒，或者称Gr2是Gr1的子粒，记为Gr2pGr1。

性质2 对于任意组合粒Gr = (w, h(w))，其中w = (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，满足GrpN，其中，N∈Dec(Gr)。

证明：由N∈Dec(Gr)，所以令N = ((ai, Mi), h(ai, Mi))，因为w∧(ai, Mi) = w，所以Gr∧N = Gr；又有w∨(ai, Mi) = (ai, Mi)，所以Gr∨N = N。由定义6得GrpN。

三、粒的分层结构

定义7 （粒子空间） 设U为有限对象集，G为有限原子粒集合，原子粒((a, M), h(a, M))∈G，X，X1，X2⊆U，B，B1，B2⊆G，f：ϑ(G)→ϑ(U)为粒集到对象集的映射算子；g：ϑ(U)→ϑ(G)表示从对象集合到粒集上的映射算子。若f-满足：

且g满足：

则称GCs = (U, G, I)为粒子空间，其中I = U×G表示对象与粒之间的二元关系。对于任意粒子Gr∈G，x∈U，若(x，Gr)∈I表示对象x满足粒Gr，若(x，Gr)∉I表示对象x不满足粒Gr。

性质3 对粒子空间GCs = (U, G, I)，令X，X1，X2⊆U；B，B1，B2⊆G，则有

证明：

（1）已知B1⊆B2，则f(B1∪B2) = f(B2)，又由粒子空间的定义知f(B1∪B2) = f(B1)∩f(B2)，所以f(B2) = f(B1)∩f(B2)，而f(B1)∩f(B2)⊆f(B1)，因此f(B2)⊆f(B1)，同理有X1⊆X2⇒ g(X2) ⊆g(X1)。

（2）类似于（1）的证明。

（3）由于B1∩B2⊆B1，B1∩B2⊆B2，则由性质（1）可得f(B1∩B2)⊆f(B1)，f(B1∩B2)⊆f(B2)，所以f(B1∩B2)⊆f(B1)∪f(B2)成立。

定义8 在信息系统S = (U, A, V, F)中，对于任意粒Gr = (Ψ, h(Ψ))，其中Ψ = (a1, M1)∧(a2, M2)∧…∧ (an, Mn)，Dec(Gr) = {Gr1, Gr2, …, Grn}，该粒在信息系统S中对应的粒子空间可以表示为(U’, G, I)，其中U’ = U – {x|(x, Gri)∉I , Gri}，Gri∈Dec(Gr)}，G = Dec(Gr)。定义9 在信息系统S = (U, A, V, F)中，粒Gr对应的的粒子空间为GCs = (U, G, I)，对于一个二元对（B, f(B)），其中B⊆G，如果满足B = g(f(B))，则称该二元对为该粒子的子粒节点。

定理2 在信息系统S = (U, A, V, F)中，对于任一给定二元对(Bn-1，Xn-1)其中Bn-1⊆G，Xn-1⊆U，经以下有限次迭代运算：

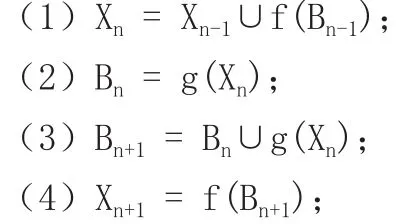
则必然存在一子粒节点(Bn’，f(Bn’))与之对应。

证明：显然运算中Xn是单调增加的，又因为论域U是有限集，必然存在Xn’= Xn’+1⊆U由运算（1），使得Xn’= Xn’+1= Xn’∪f(Bn’)，由运算（2）Bn’= g(Xn’)，又由运算（3）有Bn’= Bn’∪g(Xn’) = g(Xn’)，又因为Xn’= Xn’+1，所以Bn’= g(Xn’+1)，再由运算（4）可得Xn’+1= f(Bn’+1)，于是(Bn’，f(Bn’))为一子粒节点。

定义10 在信息系统S = (U, A, V, F)中，粒Gr对应的的粒子空间为GCs = (U, G, I)，设P = {(B, f(B))|B∈G, B = g(f(B))}为GCs中所有子粒节点的集合，则存在唯一偏序集(P, p)与之对应，且该偏序集中子粒节点都存在唯一的最小父粒（下确界）和一个唯一最大子粒（上确界），这个偏序集产生的数据结构称为Gr在信息系统S中的投影。

在一个粒子对应的粒子空间中，对于每个子粒节点总是存在一个唯一的最小下确界和一个唯一的最大上确界。由此得到该粒子在相应信息系统中的投影。显然这个投影描述出的是一个特征粒在某个信息系统中的具体层次结构。如果将其所有子粒节点按照父粒在上，子粒在下的原则用线段连接起来就得到该特征粒的层次结构图。

四、结束语

本文试图从应用的角度构建粒的结构，为了满足应用的需求，对粒的表示方法加以改进，从而使粒计算更具适用性，进而构建粒子空间，并将粒子空间投影到信息系统中得到其分层结构图，从而满足用户对数据局部分析或概化分析的兴趣点，并尝试通过这种粒结构来协助用户进行知识检索，构建基于新的粒结构的知识检索的具体模型及系统功能的设计与实现。

[1] 苗夺谦, 王国胤, 刘清, 林早阳, 姚一豫. 粒计算：过去、现在与展望[M]. 北京: 科学出版社, 2007.

[2] 徐久成, 史进玲, 张倩倩. 基于粒计算的序决策规则提取算法[J]. 模式识别与人工智能, 2009, 4(4)：660-665.

[3] 王国胤, 张清华. 不同知识粒度下粗糙集的不确定性研究[J]. 计算机学报, 2008, 31(9): 1588-1598.

book=118,ebook=118