Lorenz超混沌系统的周期扰动与激励控制

李贤丽,张笑宇,王 升,张秀龙,严晓波

(1.东北石油大学电子科学学院,黑龙江大庆 163318; 2.大庆油田昆仑集团有限公司,黑龙江大庆 163453)

Lorenz超混沌系统的周期扰动与激励控制

李贤丽1,张笑宇2,王 升1,张秀龙1,严晓波1

(1.东北石油大学电子科学学院,黑龙江大庆 163318; 2.大庆油田昆仑集团有限公司,黑龙江大庆 163453)

对非线性Lorenz超混沌系统进行数值计算,得到系统随参数变化的分岔图和动力学性质,系统只存在1个不稳定定点和复杂的超混沌运动;采用周期扰动和周期激励无反馈控制方法对系统的超混沌运动进行控制.结果表明:均可将系统的超混沌运动控制为规则的周期运动,实现对复杂Lorenz超混沌系统的控制,控制结果受系统自身的动力性质影响较大,控制后系统产生新的动力学行为.该方法扩展了周期扰动控制方法的适用范围,可为采用无反馈控制方法控制超混沌运动的研究提供参考.

Lorenz系统;超混沌系统;超混沌控制;无反馈;周期扰动;周期激励

0 引言

自然界中广泛存在混沌现象,混沌运动具有复杂性、普适性和遍历性.混沌控制是混沌应用的关键环节,由于混沌控制在工程技术上具有重大研究价值和诱人的应用前景,使其成为非线性科学研究的热点.

自1990年OttE,GrebogiC和YorkeJA提出OGY方法[1]实现混沌控制以来,研究者提出许多控制混沌运动的方法,如自适应控制法[2]、参数周期扰动控制法[3]、周期激励控制法[4]、周期脉冲控制法、偶然正比反馈(OPF)控制法[5]、线性反馈控制法等,在实验和实际工程中得到了应用.混沌运动控制方法可分为反馈控制法和无反馈控制法,2种方法各具优缺点,适用条件也不尽相同.反馈控制法的输入可以根据受控系统的具体状态进行调节,具有微扰较小的优点,前提是需要预先了解系统的运动状态,而实际的非线性系统难以预先了解系统的动力学特性[6].无反馈控制法不需要测量状态变量,控制方法简便易行,已在电力系统、振动系统等领域得到应用.无反馈控制法应用于非自治系统的混沌控制较成熟,效果明显,很小的控制输入即可改变系统状态,但在自治系统的混沌控制应用较少.对Rossler、CHAY系统,李贤丽等[7-8]采用参数周期扰动法、周期激励法、周期脉冲法等无反馈控制方法,实现了较好的控制.

由于超混沌系统有多个正的李雅普诺夫(Lyapunov)指数,使超混沌运动具有高度复杂性和轨道极端不稳定性,此外,系统包含更加丰富的动力学信息,使超混沌控制比混沌控制更为复杂,因而在保密通信等方面比混沌系统具有更高的应用价值,对其实现控制有着更为深远意义.近年来,超混沌控制的研究取得了许多成果,如线性反馈控制法[9]、延迟变量反馈法[10]、同步控制法[11],以及常数脉冲与自适应脉冲的混合控制法[12]等,实现了超混沌系统的控制,但控制方法多数为反馈控制方法,无反馈控制方法研究很少.笔者选取参数周期扰动法和周期激励法等无反馈控制方法,对Lorenz超混沌系统[11,13]的混沌运动进行有效控制,扩展周期扰动控制方法的适用范围,对非线性动力学系统的超混沌控制研究有一定意义.

1 模型及动力学性质

1.1 模型

Lorenz在研究大气气候模型时,得到一个简化的三维非线性微分方程组,其数值解产生了复杂的混沌运动.该方程形式为

式中:a,b,c均为参数.当a=10,b=8/3,c=28时,系统处于混沌运动状态.

Lorenz等对天气、对流、水轮机、发电机、激光器等真实物理系统的研究发现,Lorenz系统可以作为许多现实混沌运动的精确模型.

Lorenz超混沌系统是在Lorenz系统基础上修改得到,为四维非线性微分方程组,具体形式[13]为

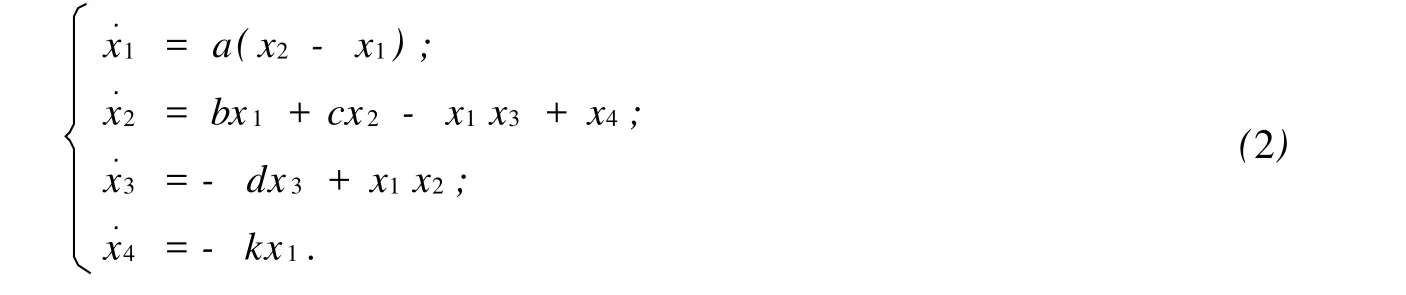
式中:d,k均为参数.

1.2 动力学性质

取参数b=7,c=12,d=3,k=5时的Lorenz超混沌系统,采用四阶龙格—库塔算法,对系统方程式(2)求数值解,得到系统随参数a变化分岔结构图(见图1),其中部分放大的精细结构见图1(b).由图1可得,当17.0≤a≤17.4时,为1周期轨道;当21.6≤a≤21.8时,为3周期轨道;当46.6≤a≤85.8时,为5周期轨道;当85.9≤a≤88.5时,为7周期轨道.在混沌带中镶嵌有较宽的3周期和5周期运动的窗口,说明此系统的3周期和5周期运动比较稳定,当a=21.7和53.0时,可得系统的时序图和相图,系统分别处于3周期和5周期运动状态(见图2和图3).

图1 x1max随参数a变化的分岔图

图2 a为21.7时3周期时序图和相图

图3 a为53.0时5周期时序图和相图

由稳定性分析可得,系统仅有一个定点(0,0,0,0),定点领域线性化方程的Jacobi矩阵为

当a=35时,系统的特征值λ满足

可得其特征值λ1=-39.8133;λ2=16.5477;λ3=0.2656;λ4=-3.0000.

因此(0,0,0,0)为系统的不稳定定点,且在2个方向上不稳定.系统有2个正的Lyapunov指数,处于超混沌状态,系统时序图和相空间图见图4,形成复杂的奇怪吸引子.

图4 a为17时超混沌状态时序图和相空间图

2 混沌控制方法

2.1 参数周期扰动

参数周期扰动控制法是在系统的某个参数上施加周期性的扰动实现抑制混沌运动的一种方法[3].在方程式(2)中,选取对系统运动状态影响较大的参数a作为控制参数并对其加入周期扰动,即把方程式(2)的a改为a′,形式为

式中:r为扰动的振幅;ω为参数扰动频率(ω=2π/t0,t0为周期).可以通过调节控制参数r和ω实现混沌控制.

2.2 周期激励

周期激励法是通过给系统附加周期变化的作用力实现非线性动力学体系的混沌运动状态的一种方法[4].在方程式(2)的第1式右侧加入周期激励项F,形式为

式中:r和ω分别为激励振幅和激励频率.可以通过调节控制参数r和ω,实现混沌控制.

2种方法是依据混沌运动对初始条件的高度敏感性、轨道的遍历性和混沌吸引子中镶嵌有无穷多个不稳定周期轨道的性质及共振原理,通过对系统施加弱周期扰动实现对混沌运动的控制.

3 超混沌控制

在Lorenz超混沌系统中,取参数a=35,b=7,c=12,d=3,k=5时的超混沌运动进行研究,分别采用参数周期扰动和周期激励方法对Lorenz超混沌系统的超混沌运动进行控制.

3.1 周期扰动

在Lorenz超混沌系统中选取参数a作为控制参数,对其加入周期扰动,即将式(2)改为

计算结果表明,当ω=3.3时,改变控制振幅r可以得到稳定控制.系统随扰动振幅r变化的控制图见图5.当r取特定范围时,系统的超混沌运动成为规则的周期运动,从而实现控制.当参数0.58≤r≤0.66时,系统能够被稳定控制到5周期运动,系统相图见图6.

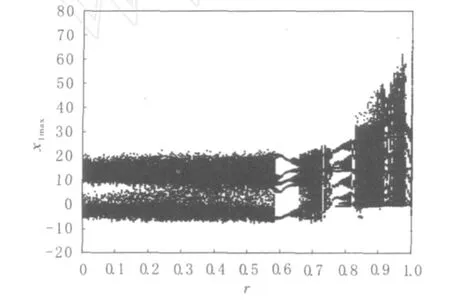
图5 ω为3.3时参数周期扰动控制

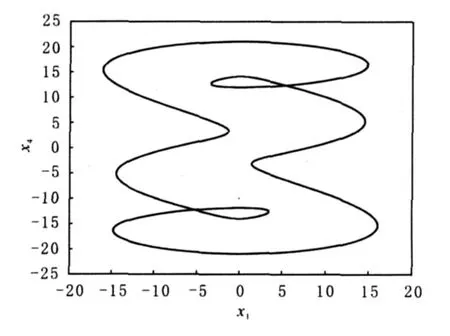
图6 0.58≤r≤0.66时5周期相图

3.2 周期激励

在Lorenz超混沌系统方程式(2)中加入附加的周期激励项F实现控制动力学体系的超混沌态,其形式为

计算结果表明,当ω=2.95时,对控制参数r循环运算,控制结果随r变化见图7.当控制参数r取特定范围时,系统的超混沌运动成为规则的周期运动.当29.75≤r≤32时,能有效地将混沌控制到3周期运动.r=30时系统相图见图8.

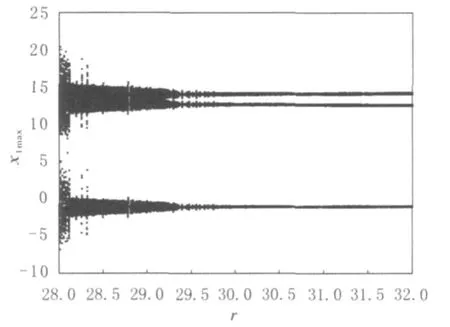
图7 ω为2.95时参数周期激励控制

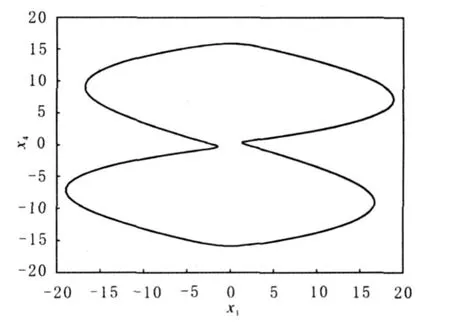
图8 r为30时3周期相图

周期扰动和周期激励控制方法对超混沌运动的控制较易控制于3周期和5周期运动,其原因是系统本身的3周期、5周期运动较稳定,因此系统本身的动力学性质对超混沌控制影响较大.由于超混沌运动较混沌运动复杂得多,至少存在2个或2个以上不稳定方向,因而在实际控制中,可控参数较难确定且范围较小,更加难于控制.将原系统相图(见图2)和控制后得到的相应周期相图(图6和图8)比较可知,控制得到的稳定周期轨道并不是原系统的周期轨道,仅运动周期与原系统运动周期相同,而系统的动力学性质发生变化,产生新的动力学行为.

4 结论

(1)参数周期扰动与周期激励控制可实现对Lorenz超混沌系统的超混沌运动的有效控制,使其转变为规则的周期运动,说明2种方法对超混沌控制有效.

(2)超混沌运动相对混沌运动更为复杂,更加不易实现稳定控制,实现超混沌控制实际困难较大,如可控参数范围较小、不易确定等.

(3)系统本身的动力学性质对控制结果影响较大,某些周期运动较易控制(如3周期、5周期等).

(4)周期扰动控制法无需预先知道体系的性质,即可对体系的超混沌运动状态进行控制,控制得到的稳定周期运动不再是原系统的周期运动,系统的动力学性质发生改变,能够得到丰富的信息及新的动力学行为.

[1] OttE , Grebogi C , Yorke J A. Controlling chaos[J ] . Phys. Rev. Lett. , 1990 ,64 (11) :1196 - 1199.

[2] Sinhna S , Ramaswamy R , Subba R J . Adaptive control in nonlinear dynamic[J ] . Physica D. , 1990 ,43 :118 - 128.

[3] Lima R , Pettini M. Suppression of chaos by resonantparametric perturbations[J ] . Phys. Rev. A. , 1990 ,41 :726 - 728.

[4] Braiman Y, Goldhirsch I. Taming chaotic dynamic with weak perturbation[J ] . Phys. Rev. Lett. , 1991 ,66 (20) :2545 - 2548.

[5] Peng B , Petrov V , Showalter K. Controlling chemical chaos[J ] . J . Chem. Phys. , 1991 ,95 :4957 —4963.

[6] 方锦清.非线性系统中混沌控制方法、同步原理及其应用前景(二)[J].物理学进展,1996,16(2):137-201.

[7] 李贤丽,李贤善,赵逢达.Rossler系统的混沌控制[J].大庆石油学院学报,2004,28(3):106-108.

[8] 李贤丽,赵逢达,李贤善.非线性自治系统快速混沌控制方法[J].大庆石油学院学报,2004,28(3):106-108.

[9] 尹逊和,冯汝鹏.超混沌系统的控制[J].原子能科学技术,2000,34(5):432-437.

[10] 陈菊芳,程丽,刘颖,等.延迟变量反馈法控制离散混沌系统的电路实验[J].物理学报,2003,52(1):18-24.

[11] 朱夜明,乔宗敏.Lorenz超混沌系统的全局同步控制[J].合肥工业大学学报,2007,30(8):1007-1009.

[12] 陈光平,郝加波.超混沌Lorenz系统的常数脉冲与自适应脉冲的混合控制[J].物理学报,2009,58(5):2914-2920.

[13] 王兴元,王明军.超混沌Lorenz系统[J].物理学报,2007,56(7):5136-5141.

Periodical perturbation and excitation controll ing of hyperchaotic Lorenz system/ 2010 ,34( 4) :105 - 109

LIXian-li1,ZHANGXiaoyu2,WANGSheng1,ZHANGXiu-long1,YANXiao-bo1
(1.Electronic Science College , NortheastPetroleum University , Daqing , Heilong jiang 163318 , China;2. Kunlun Group Co. of Daqing Oil field , Daqing , Hei long jiang 163453 , China)

Through numerical calculation of hyperchaotic Lorenz system , we obtained the bifurcation diagramand dynamics behavior of the system by changing the parameters. According to the stability theory, there existonly one unstable fix pointand complex hyperchaotic motion. Two kinds of methods fornon - feedback control , parameter sperturbation and periodic excitation , are used to control hyperchao s.With the two methods , we realized the conversion of the hyperchaotic motion to regular (periodic) motionfor some ranges of valves of choosing parameters and controlling of complex hyperchaotic motion.Controlling results are influenced by dynamic Character of the system and new dynamic behavior is produced.The study extends the scope of period perturbation control method and provides reference for thenon-feedback control methods to control chaotic motion of hyperchaotic motion.

controlling chaos;hyperchaos;lorenz system;non-feedback;periodsper turbation;periods excitation

book=4,ebook=313

TP273

A

1000-1891(2010)04-0105-05

2010-08-20;审稿人:白永强;编辑:任志平,张兆虹

黑龙江省教育厅科学技术研究项目(11551023)

李贤丽(1971-),女,副教授,主要从事非线性动力学及混沌控制方面的研究.