混凝土早期热-力学模型及工程应用
张 研,蒋林华,储洪强
(1.河海大学力学与材料学院,江苏南京 210098)
大体积混凝土的广泛应用使得温度开裂的发生日益严重,同时高强混凝土的出现使结构早期温度应力显著增加,因此工程技术人员越来越关注早期混凝土热学和力学性质[1-5],以便能够进一步从理论上分析混凝土结构温度和应力的变化规律,并对温度变化导致的开裂破坏进行预测。笔者在混凝土结构早期温度场的计算中,用等效时间的概念定义混凝土绝热温升,同时考虑化学反应速率对混凝土绝热温升过程的影响,给出了考虑化学反应速率的混凝土绝热温升和热传导方程及其解法。同时,在混凝土应力应变关系中,在通常温度应力的基础上考虑了混凝土早期强度与水化程度之间的影响,探讨了应力、绝热温升以及水化程度之间的关系。在等效时间理论的混凝土非线性热传导方程和混凝土早期强度理论研究的基础上,采用数值手段对苏州轨道交通车站大体积混凝土施工期温度应力与温度控制进行探讨。
1 温度控制方程与混凝土早期强度理论
1.1 温度控制方程
假定混凝土在浇筑过程中满足能量守恒定律,并且考虑混凝土自身水化热,则混凝土三维不稳定温度场热传导方程可以表示为
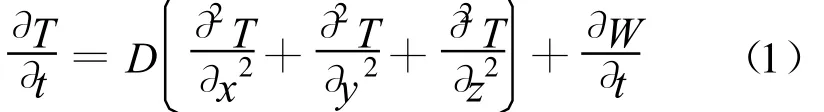
式中:x,y,z为直角坐标;t为时间;T(x,y,z,t)为温度场;D为混凝土导温系数,D=λ/cρ(λ,c和ρ分别为混凝土的导热系数、比热容和密度);W为混凝土自身在绝热条件下的水化热。
在此,引入等效时间的概念来描述混凝土的绝热温升,混凝土三维不稳定温度场的热传导方程可以表达为

式中:θeq为绝热条件下水化热的等效温度,其与等效时间te相关联;θu为最高绝热温升;M为参数,用来控制温度变化速度。
由于在水泥水化热绝热温升中应用了等效时间概念,可以考虑环境温度对混凝土绝热温升的影响,以更好地反映混凝土的实际工作状态,详见文献[6]。
1.2 等效时间的定义
水泥在凝结过程中体现出化学放热反应,研究表明[7-8],化学反应速率随着温度的升高而加快。根据试验结果拟合,对于混凝土水化反应过程,温度对水化反应速率的影响服从Arrhenius方程:

式中:k为化学反应速率;T为绝对温度;E为与化学活动能有关的常数;R为气体常数。
从式(4)可以看出,在温度分别为T1和T2时,水化热化学反应速率比k1/k2可表示为

从式(5)计算可得,当水化热温度分别为10℃,20℃,30℃,40℃时,水泥的k1/k2分别为2.51,5.94,13.30和28.31。也就是说,温度对水泥水化热化学反应速率有很大的影响。由此看出,混凝土早期的温度发展很大程度上依赖于混凝土的温度条件。
Bazant[9]根据Arrhenius方程提出了成熟函数,并提出用参考温度Tr_来计算te,即
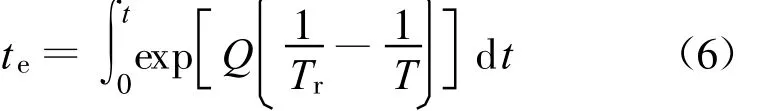
式中:Q定义为化学活动能与气体常数之商,Q=E/R;T为在时间间隔 Δt内混凝土的平均温度。应用R时,Tr和T需要采用绝对温度,其中Tr为绝对温度293℃。
式(6)被用来定量计算养护时间和温度对混凝土的影响。根据不同的使用条件,其离散形式可以表示为

混凝土三维不稳定温度场的热传导方程中采用Bazant提出的有效时间概念的离散形式进行数值仿真计算。通过有限单元法对非线性热传导方程(式(2))进行求解,计算混凝土结构中的温度场。由于混凝土导热系数很低,所以混凝土结构早期的中心温度将高于其表面温度,这将导致结构不同位置具有不同的水化热化学反应速率,采用等效时间概念可以较好地体现不同温度对水化热化学反应速率的影响;同时,由于不同外界温度条件的影响,不同季节施工的混凝土具有不同的外界温度和初始温度,也将导致不同的水化热化学反应速率。
1.3 混凝土早期强度与温度应力理论
闫东明等[10]试验研究表明,混凝土材料在高围压状态下体现更高的破坏强度以及塑性为主的应变特征。在城市建设工程中的结构受力特征相对简单,主荷载方向以外的实际荷载在数兆帕范围,一般不存在非主应力方向上的高应力状态。因此,弹脆性特征是混凝土在此情况下最主要的力学特征,同时混凝土材料的工作环境(荷载)必须小于其破坏荷载,不需要考虑混凝土材料破坏以后的脆性失效特性。综合以上,本文采用弹性本构模型来反映混凝土的应力应变关系,即

式中:σ为应力;C为混凝土有效弹性模量;ε为应变。
混凝土早期强度随着水化过程的进行不断地增加,并最终达到稳定。因此,采用与水化时间相关的函数来表达混凝土有效弹性模量[6,11]:

式中:C0为混凝土28d时的弹性模量;φ,α和b为模型参数,用来控制弹性模量的增加。可以看出,有效弹性模量随着时间迅速增加,并最终稳定为C0。
当采用增量形式的应力应变关系时,有


式中:ΔPe,ΔPt和 ΔPv分别为增量步 Δt内外荷载增量、温度变化引起的变温荷载增量以及徐变引起的荷载增量;εt和εv分别为温度应变增量和徐变应变增量[12];εv0,εv1,A0,A1,b0,b1,R0,R1,τ为参数,可以通过试验资料或以往的工程经验确定。
1.4 温度场和应力场有限元计算方法
为了求解基于等效时间的非线性热传导方程(2),首先在空间域上分解成有限个区域,根据Galerkin法原理得到有限元整体控制方程,即[1,6]

在时间域采用有限差分法计算,最后形成求解非稳定温度场的有限元差分支配方程,即

通过式(12),可以根据t-Δt时刻的温度场求解t时刻的温度场。根据温度场求解的各节点时间以及温度变化,代入式(10),获得各点应力增量。
2 车站主体结构的仿真研究
苏州轨道交通工程是苏州市重点市政建设项目之一,该工程分为车站主体以及隧道段。隧道段双路通过,采用盾构开挖形式,车站主体为地下2层2跨,扩大段为2层4跨,系现浇钢筋混凝土结构,采用明挖顺作法施工。本研究以代表性车站主体2层2跨结构进行研究。车站主体结构由围护地下墙(永久性结构)、楼板、柱和墙体组成的复合墙结构组成。车站内部结构柱混凝土强度等级为C40,其余结构柱及地下连续墙、内衬、梁、板和墙混凝土强度等级为C30;地下墙、内衬、车站顶板和底板抗渗标号大于或等于S8。为了降低混凝土的水化热,防止发生有害裂缝和减小裂缝宽度,车站大体积浇筑的混凝土采用双掺低水化热水泥,水泥用量低于280kg/m3,水泥熟料与矿渣之和不小于300kg/m3。在混凝土浇筑初期,温度和温度应力随时间急剧变化,而混凝土的水化热、弹性模量、徐变度等基本参数随混凝土龄期改变,因此大体积混凝土结构的温度应力计算是一个复杂的问题。
2.1 基础资料
2.1.1 温度资料
考虑到苏州市多年平均温度所具有的代表性,选用近5年来苏州月平均温度作为外界温度条件,见表1。

表1 苏州多年各月平均气温 ℃
2.1.2 荷载资料
车站主体为开挖浇筑,主体完工后两侧受到土体自重产生的侧压力,地基土为中软土,密度为1800kg/m3。所用混凝土根据不同强度,自重在2400~2700 kg/m3范围。在主体运行期,结构承受不大于20kPa的荷载作用。与水化热产生的温度应力相比,车站主体运行期承受的荷载作用可以忽略不计。
2.1.3 材料参数
根据相关混凝土进行了绝热温升试验,C30和C40混凝土绝热温升分别为 55℃和59℃。混凝土和土体的主要热力学参数见表2。

表2 各分区材料主要物理参数(28d)
2.2 仿真计算结果分析
对车站主体典型断面进行三维仿真,图1中显示的是车站主体西区的结构,外侧是未开挖的土体,不同的颜色表示不同的部位,并用来区别浇筑过程中的先后顺序。该三维实时模拟过程反映实际浇筑情况,预计在7月初开始浇筑,浇筑顺序为边墙、底板、底柱、中板、上柱、顶板、上下墙、回填混凝土等。浇筑1d后拆模,表面采取保温措施。三维有限元施工期和运行期仿真温度和应力见图2。采用Gid软件对数值计算结果进行图形绘制。此软件可以考虑实际浇筑批次对图形单元进行单独或同时显示,因此,不同日期反映出的车站主体结构因为当时的浇筑情况而显示出不同的几何形状。图2显示的是浇筑过程中可能出现的温度以及应力较大情况下的典型日结果。

图1 车站整体三维有限元网格示意图
根据数值仿真计算,得到以下分析结果:
a.混凝土浇筑后2~3d,新浇混凝土出现较大的拉应力,在表面采取保温措施的情况下,板体最大拉应力达到2.0MPa,墙体最大拉应力达到2.6MPa,达到并超过龄期为3d的混凝土抗拉强度。早期温度裂缝的产生不可避免。因此,在采取表面保温措施的同时,必须使用混凝土外加剂来降低水化热或提高早期混凝土强度,这样混凝土底板表面裂缝可以得到一定范围的控制。
b.在混凝土浇筑过程中,板、柱、墙交界的角点处由于结构形式的突变,产生应力集中,拉应力在混凝土浇筑过程中达到2.0MPa,达到了混凝土早期的抗拉强度,裂缝首先在表面产生。随着龄期的增加,拉应力将逐步转变为压应力,从而使裂缝闭合。为了避免该处裂缝扩展为贯穿性裂缝,建议在界面突变处增加钢筋以提高混凝土的局部承载能力。
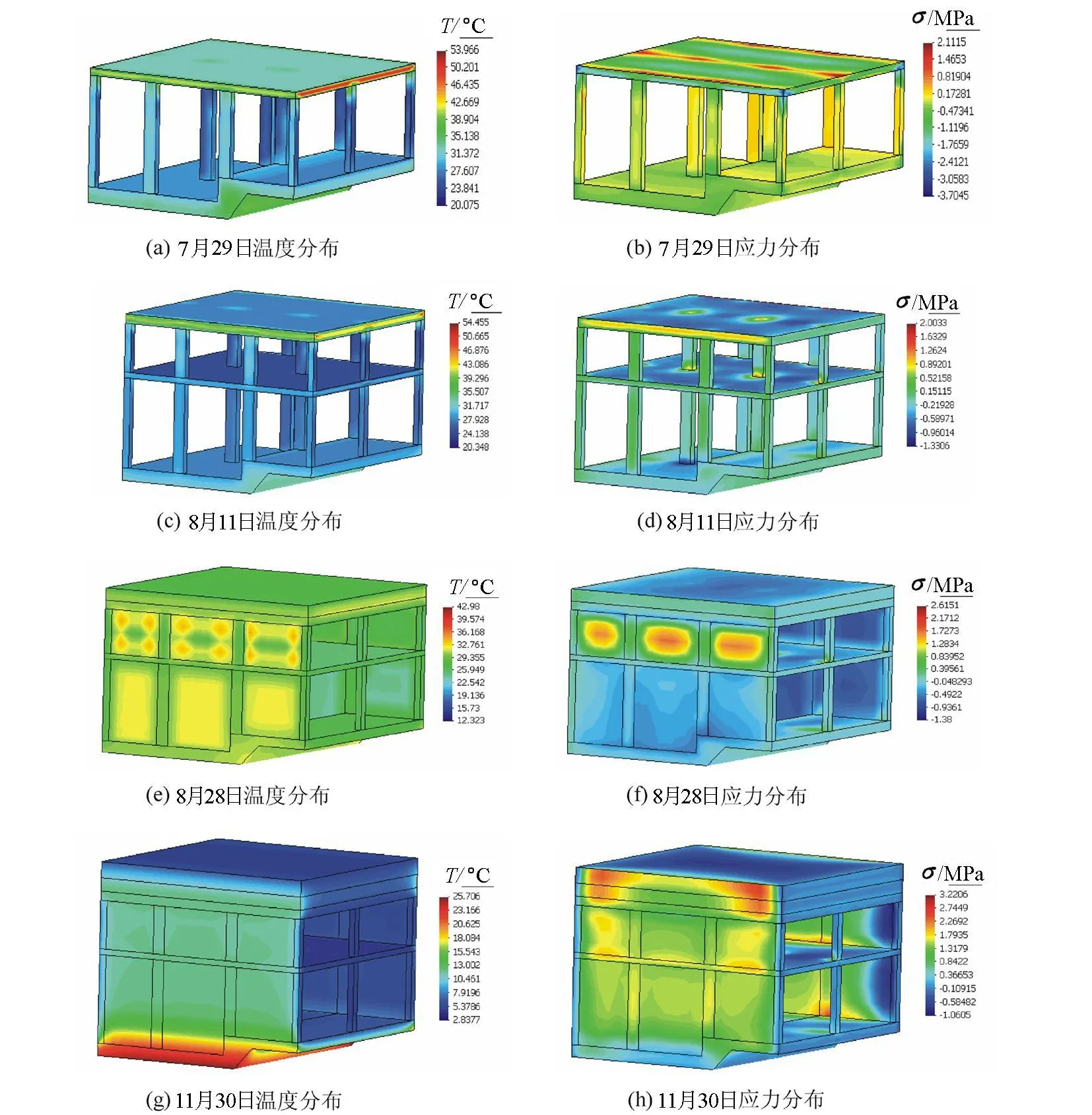
图2 浇筑过程中不同时刻的温度T及应力σ分布
c.混凝土最高温升为浇筑温度与水泥水化热温升之和,夏季施工中降低浇筑温度对降低最高温升有重要意义。但是对于该工程混凝土浇筑,单独采用降低浇筑温度的做法效果有限。分析认为:当构件的厚度在几十厘米范围内时,热量可以较快地从构件表面吸收或散发,从而降低了浇筑温度的作用。最高温度达到54.45℃的情况发生在8月11日。当时气温在27℃左右,同时最高温度出现在顶板的中间层与顶柱接头处,此处有可能因为顶板未与空气接触而减缓了放热过程,从而比顶板其他部位的温度高了10℃左右。因此,建议在夏季施工过程中采取表面保温养护措施,以提高温控效果。
d.车站主体工程温控的重点是边墙。在浇筑3d后,边墙产生的拉应力可达到2.6MPa,超过混凝土3d的抗拉强度。这是由挡土墙对边墙的约束引起的,建议在边墙与挡土墙之间采取隔离措施,以降低挡土墙对边墙的约束,从而降低应力,有效解决边墙的开裂问题。
e.在运行期,随着不同季节气温的变化,车站主体应力呈周期性变化。笔者在数值仿真过程中考虑了调温设施丧失下车站最不利的温度情况。冬季时车站主体发生最大拉应力,板体最大拉应力为3.4MPa,墙体最大拉应力为3.0MPa。中板的最大拉应力受气温影响不大。这是由于结构形状突变对应力的影响远大于温度变化的影响。但因为在运行期,混凝土抗拉强度也相应提高,不易发生开裂。
3 结 语
在介绍等效时间概念的温度控制方程及其混凝土早期强度理论的基础上,结合有限元方法对苏州某地下车站进行了温度场及应力场的三维仿真,对仿真结果进行了分析,并对工程实施提出了改进措施。三维仿真结果表明,常规的温控
[措施对于该车站结构温度裂缝的限制效果不明显,降低混凝土水化热和提高混凝土早期强度是防止温度裂缝最有效的办法。本文主要从理论和数值上分析混凝土早期热-力学性能对大体积混凝土结构的影响,对于材料参数的确定主要采用以往工程的经验。因此,对于混凝土早期热 力学模型中材料参数的精确确定需要进行进一步的试验研究。
:
[1]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1999.
[2]张子明,郭兴文,杜荣强.水化热引起的大体积混凝土墙应力与开裂分析[J].河海大学学报:自然科学版,2002,30(5):12-16.
[3]冯树荣,胡志奇,何建平,等.基于施工条件的龙滩碾压混凝土重力坝温度应力仿真分析[J].河海大学学报:自然科学版,2009,37(1):57-61.
[4]宋智通,张子明,陈金杭.基于细观尺度的混凝土绝热温升预测[J].河海大学学报:自然科学版,2008,36(6):819-823.
[5]郑丹,李文伟.预测全级配大坝混凝土弹性模量的三相模型[J].水利水电科技进展,2009,29(4):14-17.
[6]张子明,宋智通,黄海燕.混凝土绝热温升和热传导方程的新理论[J].河海大学学报:自然科学版,2002,30(3):1-6.
[7]de LARRARD F,ACKER P,ROY R L.Shrinkage creep and thermal properties[C]//SHAH S P,AHMAD S H.High Performance Concrete:Properties andApptications.New York:McGraw Hill Inc,1994:65-114.
[8]COPELAND L E,KANTRO D L,VERBECK G.Chemistry of hydration of portland cement[C]//United States Department of Commerce.Proceedings of Fourth International Symposium on the Chemistry of Cement.Washington D.C.:Prtland Cement Association,1960:429-465.
[9]BAZANT Z P.Constructive equation for concrete creep and shrinkage based on thermodynamics ofmulti-phase system[J].Materials and Structures,1970,3(1):3-36.
[10]闫东明,林皋.三向应力状态下混凝土强度和变形特性研究[J].中国工程科学,2007,9(6):64-70.
[11]TANK R E,CARINO N J.Rate constant function for strength development of concrete[J].ACI Material Journal,1991,88(1):74-83.
[12]BAZANT Z P.Prediction of concrete creep effects using ageadjusted effective modulus method[J].ACI Material Journal,1972,69(2):212-217.

