考虑多失效模式老龄平台结构可靠性分析

林 红,陈国明

(中国石油大学机电工程学院,山东东营 257061)

其中

考虑多失效模式老龄平台结构可靠性分析

林 红,陈国明

(中国石油大学机电工程学院,山东东营 257061)

针对老龄平台结构存在的多种退化失效因素,综合考虑疲劳失效、腐蚀失效和静强度失效这 3种失效模式,建立每种失效模式的可靠度模型,并相应给出可靠度计算方法。通过相关系数研究任意两种失效模式之间的相互影响,进而提出两种计算 3种退化失效模式全耦合作用下可靠度的方法:一是根据O.Detlevsen窄界限理论计算可靠度指标上、下限,二是通过将疲劳裂纹扩展和腐蚀退化引起的总抗力衰减引入静强度退化失效模型中,得到 3种失效模式的耦合失效概率。实际算例结果表明:在不同服役阶段构件具有不同的主导失效模式;任意两种失效模式的耦合可靠度均低于单一失效模式的可靠度,3种失效模式耦合可靠度最低。

多失效模式;相关系数;可靠性分析;O.Detlevsen窄界限理论;老龄平台

目前在世界范围内,海洋结构的老龄退化已成为一个非常广泛的问题[1-3]。由于长期服役,老龄平台结构可能存在多于一种的退化模式,这将导致平台结构出现多种不同的失效模式,如静强度失效、疲劳失效和腐蚀失效等。事实上这些失效模式之间存在一定的联系,如结构的疲劳是由于不断变化的载荷作用而引起的损伤累积过程,反过来,这一损伤的不断累积必然会降低结构的极限承载能力,从而降低结构的可靠度。因此,在对老龄平台结构进行可靠性分析时,必须考虑上述不同失效模式之间的相关性及其对可靠性的贡献。目前对多失效模式研究中,安伟光等[4]在平面桁架结构方面做了有益的工作,但是在海洋平台方面的研究较少。鉴于此,笔者考虑在波浪载荷作用下,老龄海洋平台结构可能发生的疲劳失效、腐蚀失效和静强度失效 3种失效模式,通过相关系数研究不同失效模式之间的关系,并提出两种计算耦合失效概率的方法。

1 老龄平台结构构件的可靠模型

1.1 疲劳失效

在服役过程中,海洋平台结构通常会受到疲劳交变应力的反复作用,导致平台构件所含裂纹逐步扩展。由 Paris裂纹扩展定律描述,并考虑长期应力过程,有

式中,a0为初始裂纹尺寸;ac为临界裂纹尺寸;Y为裂纹形状因子;Si为第 i个海况的应力范围;k为总的海况数;f0i为第 i个海况应力过程的跨零频率;qi为第 i个海况所占的时间百分比;C和m为材料常数,t为服役寿命。

若假设应力过程为窄带,且应力服从 Rayleigh分布,则

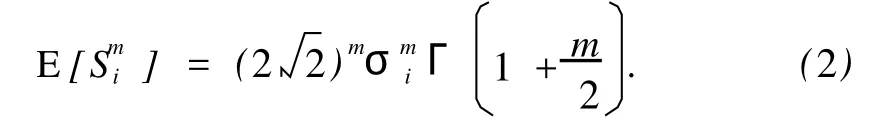
式中,Γ(·)为Gamma函数;σi=为第 i个海况中应力过程的均方根值。

通常取构件壁厚 dc表示失效时的裂纹尺寸,则疲劳失效的功能函数为

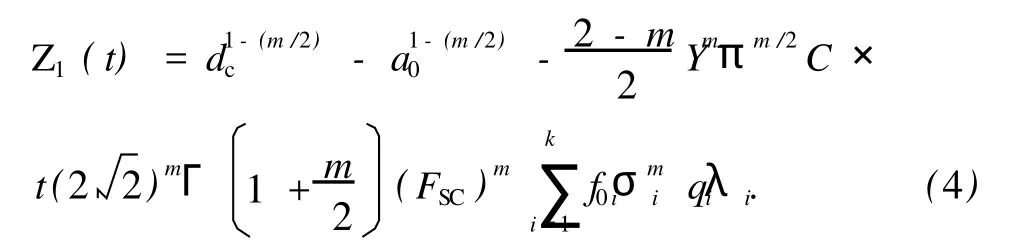
式(4)中定义的疲劳失效概率可以通过一次可靠度(FORM)/二次可靠度(SORM)方法来求解[6]。FORM和 SORM均是通过将原始的功能函数近似简化为简单函数进行处理,具有快速、高效、简洁的优点。其中,FORM方法只考虑了结构功能函数展开式的一次项,适用于功能函数非线性程度不高的情形,当函数非线性程度较高时可采用 SORM方法[7]。

1.2 腐蚀失效

海洋环境下,海洋平台结构构件的不断腐蚀也是导致其发生退化失效的一个重要因素。文献[8]将结构腐蚀损耗过程分为 4个阶段,若令 dc表示平

台构件壁厚,则功能函数 Z2表示为

式中,a,b,c,d,ca,ta,t3,rs和 cs均为相应的腐蚀参数。

1.3 静强度失效

海洋平台结构构件的静强度失效是一种瞬变型失效,其特征是一旦结构构件所受的广义载荷超过其对应的抗力,结构构件就瞬时发生破坏,因而这类失效的危险性较大。对于海洋平台结构来说,它在使用过程中受到的荷载效应及自身抗力都随时间变化,是一个随机过程。若令 S(t)为载荷效应随机过程,R(t)为结构抗力随机过程,则静强度失效的功能函数 Z3为

其中

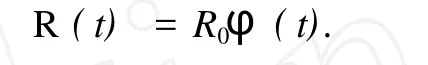
式中,R0为结构的初始抗力;φ(t)为抗力衰减函数。

由前文分析可知,平台构件的抗力衰减是由于疲劳裂纹和腐蚀两种因素引起,若分别单独考虑,则衰减函数[9]为

式中,a0和 d0分别为初始裂纹深度和腐蚀深度; a(t)和 d(t)分别为 t时刻的裂纹尺寸和腐蚀深度; dc为最大容许裂纹深度和腐蚀深度,一般取为构件壁厚;ξ1和ξ2分别为 ac和 dc所对应的最大容许强度衰减系数,且 0<ξ1<1,0<ξ2<1。

式(5)是一个时变可靠度问题,目前其计算方法并不成熟。比较简单的方法是建立离散的动态可靠性模型,即将结构的寿命周期 (0,T)平均分为 m个时段,每个时段为τ=T/m,在每个时段τ上按照静态可靠度的计算方法计算构件的可靠度。因此,海洋平台结构在(0,T)内的可靠概率 PS(T)为

若结构在第 k个时段内发生失效,则在前 1,2,…,k-1个时段内必须安全,令每个时段内载荷效应 Si的分布函数为 FSi(Si),其概率密度函数为fSi(Si),则此时结构失效概率为

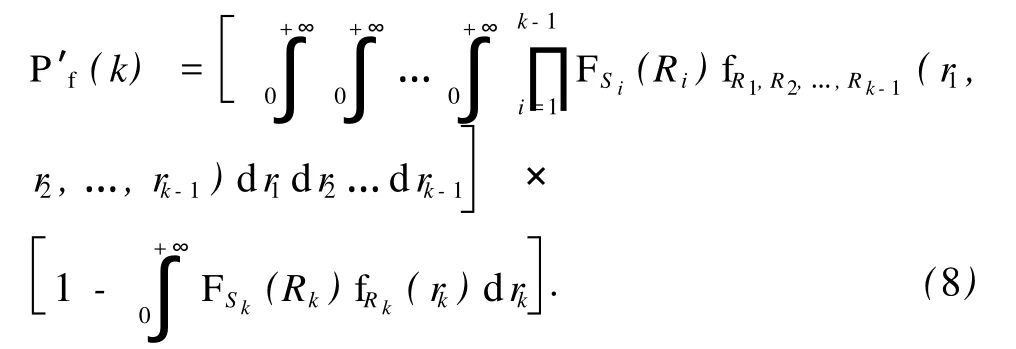
对于式 (8)第一项的处理方法[10],引入新的随机变量 SQ,将高维积分问题转化为可用FORM/SORM方法求解的常规可靠度分析问题,即

式中,fSQ(SQ)为 SQ的概率密度函数;FSQ(SQ)为概率分布函数。

由于 p{g2(·)<0}形式简单,可采用 JC法计算,式(9)的计算困难集中在第一项。若将 SQ取为前 k-1个时段中Si的最大值ST,并认为最大可变荷载效应 ST服从极值 Ⅰ型分布,则 g1(·)可表示为

式中,αT为ST极值 Ⅰ型分布的参数;Re为结构的等效抗力。

考虑抗力衰减 R(t)=R0φ(t),通过进一步简化,可得到等效抗力 Re的均值、标准差分别为

式中,φ(ti)为第 i个时间段内的抗力衰减函数。

经过上述处理,即可容易地求出每个时间段内的失效概率 P′f(k),然后根据不相容事件概率的有限可加性,可得结构在服役期内的失效概率 Pf(T)为

2 多失效模式下的老龄平台可靠性

2.1 失效模式相关性

对于任意给定的两个失效模式功能函数 Zi和 Zj(i≠j),按泰勒展开并取线性项,其相关系数可表示为

式中,Cov(Zi,Zj)为功能函数 Zi和 Zj的协方差;σZi和σZj分别为 Zi和 Zj的标准差;αi和αj分别为第 i个和第 j个失效模式功能函数的单位梯度向量。

对于向量αi的第 k个分量表示为

式中,Xk为功能函数 Zi中的第 k个随机变量;σXk为随机变量 Xk的标准差。

2.2 构件可靠性

对 3种失效模式共同作用下的失效概率计算,本文采用两种处理方法。

第一种方法是基于O.Ditlevsen窄界限理论,通过任意两种失效模式下的综合失效概率得到结构总失效概率的上下界限。

对于任意给定的两个失效模式 i和 j,结构在这两种失效模式下的耦合失效概率可表示为

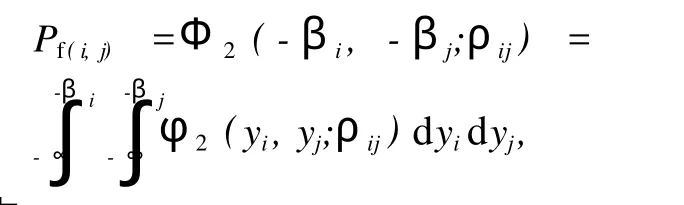
其中

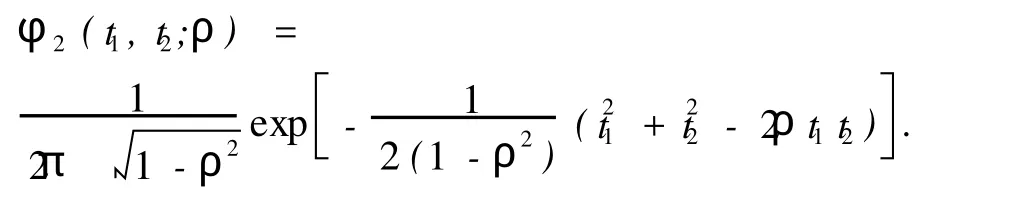
式中,φ2(·)为二元正态分布密度函数。

若构件共有m个失效模式,根据O.Ditlevsen窄界限原理,构件总失效概率 Pfs的上、下界限为[11]

第二种方法称为等效抗力衰减函数法,它将疲劳裂纹扩展和腐蚀退化引起的抗力衰减引入静强度失效模型中,即通过总的抗力衰减作用,得到构件在3种失效模式共同作用下的耦合失效概率。其中,疲劳与腐蚀共同作用导致的等效抗力衰减函数可表示为

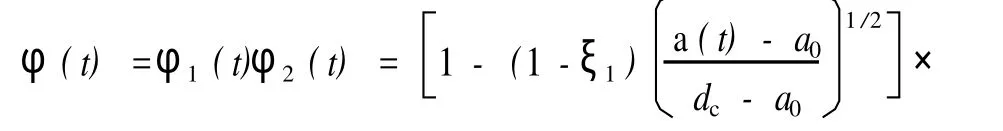
3 计算示例

3.1 平台模型及计算参数

以我国某海域一老龄平台为例,该平台为四桩腿导管架平台,设计寿命 25 a,目前已进入老龄期。应用ANSYS建立有限元模型,平台桩腿底部在泥面以下 6倍桩径处固定,平台承受自重及波浪力。本文所计算的91号单元为一横撑管单元构件,位置见图1。

图 1 平台部分有限元模型及单元位置Fig.1 FE model of platform and element position

该横撑管单元的壁厚 dc服从正态分布,均值和标准差分别为22 mm和1.2 mm;管单元的初始抗力R0考虑为其屈服强度,并认为它服从对数正态分布,均值和标准差分别为 386 MPa和 30.8 MPa。假设该管单元具有一个初始裂纹,其深度 a0服从正态分布,均值和标准差分别为 1.64 mm和 0.364 mm;形状因子Y为1.0;材料参数m为3.0;材料参数C服从对数正态分布,均值和标准差分别为 8.81×10-12和 4.84×10-12。考虑平台受到腐蚀的影响,且防腐措施效果良好,计算参数见表 1。

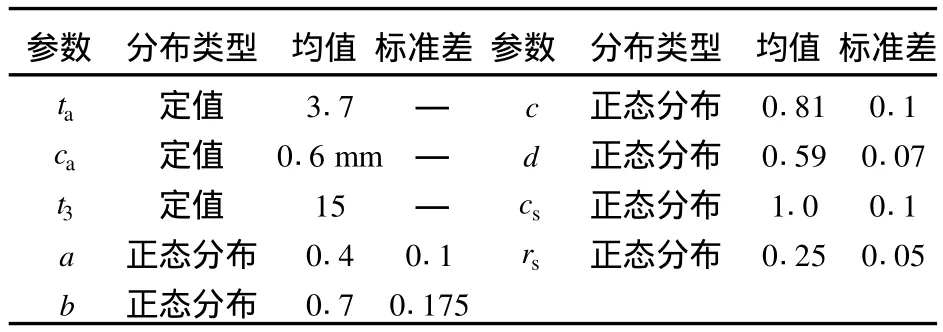
表 1 腐蚀可靠性计算参数Table 1 Corrosion reliability calculation parameters

3.2 海况描述与构件应力分析

假设本算例所考虑海况各方向统计较相近,分别考虑 0°,45°,90°和 135°四个波向的 11种海况进行疲劳应力计算,每个波向具有相同的发生概率,见表2。这样,整个服役期内的波浪载荷划分为44种静态海况,每个海况采用 P-M波谱来描述,即

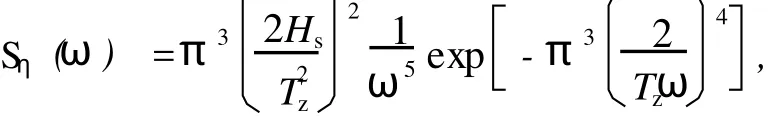
式中,Hs,Tz分别为有效波高和平均周期。

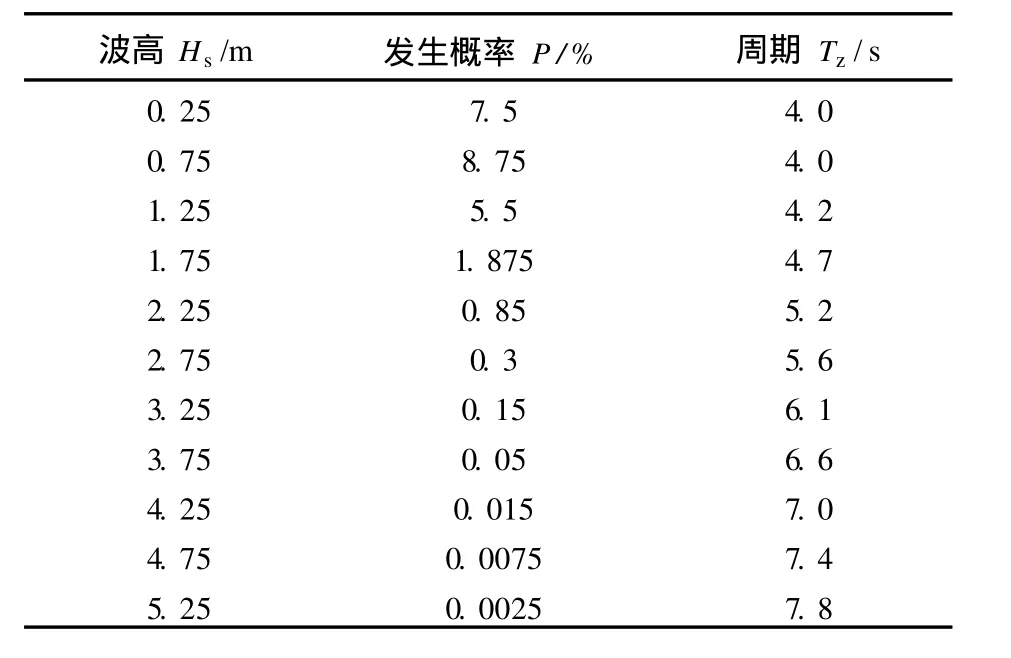
表2 波浪散布图Table 2 Wave scatter-diagram

假定一年内的最大波高 Hmax服从极值 Ⅰ型分布,即分布函数为

式中,αH和βH为分布参数,对于本文所研究的海域,αH和βH分别取 11.0和 1.63。

管单元的疲劳应力计算采用谱分析方法,通过有限元分析计算构件应力的传递函数 H(ω),然后将随机波浪谱Sη(ω)转换成随机应力谱Sσσ(ω),进而可得到构件的等效疲劳应力(管单元在极值波浪载荷下的极值应力 Smax计算方法见文献[12])。

3.3 结果分析

3.3.1 两种失效模式耦合下构件的可靠性

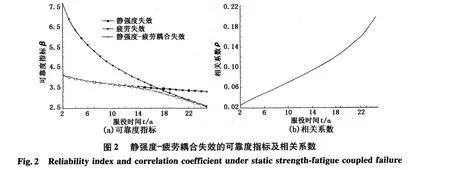
图2为静强度 -疲劳耦合失效的可靠度指标及相关系数。由图2(a)可见:在服役初期,疲劳可靠度指标高于静强度可靠度指标,这是因为这个阶段裂纹扩展量非常小,因此发生裂纹扩展失效的概率相当低,主要是由于极值载荷导致的静强度破坏;随着裂纹逐步扩展,疲劳失效的概率超过了静强度失效。对于本例计算结果,在第 17 a疲劳失效成为主要的失效模式。由此可知,对于服役多年的老龄平台来说,疲劳裂纹扩展的危害更大。由图 2(b)可见,随时间增加相关系数逐渐增大,这表明随着服役时间的增长,两种失效模式之间联系和相关性越来越密切。

图3为疲劳 腐蚀耦合失效的可靠度指标及这两种失效模式相关系数随时间变化曲线。在整个设计寿命期间,腐蚀可靠度指标一直高于疲劳可靠度指标,即疲劳退化失效将起主导作用;两者之间的相关系数很小,且两种失效模式的耦合可靠度指标与疲劳可靠度指标非常接近,图3(a)中两条曲线几乎重合。

图4为静强度 腐蚀耦合失效的可靠度指标及相关系数随时间变化曲线。在整个设计寿命期间,静强度可靠度指标一直小于腐蚀可靠度指标;两者之间的相关系数很小,且两种失效模式的耦合可靠度指标与静强度可靠度指标非常接近,图4(a)中两条曲线几乎重合。

3.3.2 三种失效模式耦合下构件的可靠性

表 3中列出了每种失效模式的可靠度指标βi(i =1,2,3)、任意两种失效模式的耦合可靠度指标βij(i,j=1,2,3,i≠j)以及根据窄界限方法计算的3种失效模式耦合的总可靠度指标上下界限βlow,βup。可见,3种失效模式共同作用下的可靠度下限比任何两种耦合的可靠度均低,且与静强度 -腐蚀耦合作用下的可靠度β23非常接近。

图 5为采用方法2(等效抗力衰减函数法)计算的 3种失效模式耦合可靠度指标与窄界限理论的计算结果对比。可见,方法 2得到的总可靠度指标与βlow非常接近。这是因为方法2通过将疲劳裂纹扩展和腐蚀两种效应引起的抗力衰减代入静强度失效模型中,从而综合考虑疲劳、腐蚀和静强度失效这 3种因素。因此,对于本文考虑的 3种失效模式,可以采 用方法 2简化计算平台构件的耦合可靠度指标。

表 3 构件可靠度指标计算结果Table 3 Calculation results of reliability index

图 5 两种方法结果对比Fig.5 Results comparison between two methods

4 结 论

(1)对于防腐效果良好的平台构件,腐蚀可靠度要比静强度和疲劳可靠度高得多;平台服役早期平台构件以静强度失效为主要失效模式,而在平台服役后期则以疲劳失效为主要失效模式;任意两种失效模式的耦合可靠度均不超过考虑单独失效模式的可靠度。

(2)总可靠度指标比任何失效模式单独作用或两两耦合作用下的可靠度均低,且与静强度 -腐蚀耦合作用下的可靠度最为接近。采用等效抗力衰减函数方法可以简化计算,且结果与窄界限方法的下界非常接近。

[1] 陈国明,刘健.近海石油老龄平台延寿技术研究[C]//中国 21世纪工程管理中心.我国近海油气勘探开发高技术发展研讨会文集.北京:c2005.

[2] GERHARD Ersdal.Assess ment of existing offshore structures for life extension[D].University of Stavanger, NORWAY,2005.

[3] GALBRA ITH D N,SHARP J V,TERRY E.Managing life extension in aging offshore installations[R]. SPE 96702,2005.

[4] 安伟光,赵维涛,安海.随机结构系统综合考虑静强度、刚度和疲劳的多失效模式的可靠性分析[J].中国科学 G辑:物理学力学天文学,2007,37(4):516-526.

AN Wei-guang,ZHAO Wei-tao,AN Hai.Reliability analysis of stochastic system considering static strength, stiffness,and fatigue[J].Science in China(Sense G): Physics,Mechanics&Astronomy,2007,37(4):516-526.

[5] TORGEIR Moan,EFREN Ayala Uraga,WANG Xiaozhi.Reliability-based service life assess ment of FPSO structures:ABS Technical Papers,2004[C].

[6] 贡金鑫.工程结构可靠度计算方法[M].大连:大连理工大学出版社,2003.

[7] ARMEN Der Kiureghian,L IN Hong-zong,HWANG Shyh-jiann.Second-order reliability approximation[J]. Journal of EngineeringMechanics,1984,113(8):1208-1225.

[8] MELCHERS Robert E.The effect of corrosion on the structural reliabilityof steeloffshore structures[J].Corrosion Science,2005(47):2391-2410.

[9] 许亮斌.近海石油平台动态疲劳可靠性分析与控制研究[D].东营:中国石油大学机电工程学院,2004.

XU Liang-bin.Analysis and control on dynamic fatigue reliability of offshore platforms[D].Dongying:College of Electromechanical Engineering in the University of Petroleum,China,2004.

[10] 赵国藩,贡金鑫,赵尚传.工程结构生命全过程可靠度[M].北京:中国铁道出版社,2004.

[11] D ITLEVSEN O.Narrow reliability bounds for structural systems[J].Journal of Structural Mechanics,1979 (17):453-472.

[12] 林红,陈国明,孙友义.基于验证载荷的老龄平台结构可靠性更新分析[J].石油机械,2008,36(9):39-42.

L I N Hong,CHEN Guo-ming,SUN You-yi.Reliability updating for aging offshore platfor ms based on proof loads[J].China Petroleum Machinery,2008,36(9): 39-42.

(编辑 沈玉英)

Reliability analysis for aging offshore platform s considering multi-fa ilure modes

L IN Hong,CHEN Guo-ming
(College of Electrom echanical Engineering in China University of Petroleum,Dongying257061,China)

Considering possible deterioration failure modes of aging platfor m members,including fatigue failure,corrosion failure and static strength failure,each reliabilitymodelwas established and the corresponding computing approach was presented.The interaction between any two failure modeswas analyzed through correlation coefficient.Then,two differentmethodswere proposed to calculate the reliability of the component under three-failure-mode-coupling.One is the O.Detlevsen´s narrow bounds theory,and the other is introducing the overall resistance deterioration including fatigue crack and corrosion to static strength failuremodel.The numerical results show that the platform member has different dominant failuremodes at different service periods.The reliability index for any two-failure-mode-coupling is lower than that of any single failure mode, and the three-failure-mode-coupling is the lowest.

multi-failure modes;correlation coefficient;reliability analysis;O.Detlevsen´s narrow bounds theory;aging offshore platforms

TE 951;TB 114.3

A

10.3969/j.issn.1673-5005.2010.04.021

1673-5005(2010)04-0107-06

2009-12-30

国家自然科学基金项目(50679083);国家“863”高技术研究发展计划项目(2006AA09Z355)

林红(1980-),女(汉族),山东聊城人,讲师,博士,主要研究方向:结构疲劳与断裂、海洋结构安全可靠性等。