采用不同湍流模型对半封闭狭缝湍流冲击射流的数值模拟

王明波,王瑞和

(中国石油大学石油工程学院,山东青岛 266555)

采用不同湍流模型对半封闭狭缝湍流冲击射流的数值模拟

王明波,王瑞和

(中国石油大学石油工程学院,山东青岛 266555)

针对海洋石油工程中废弃平台切割技术的需要,采用充分发展的入口条件结合标准壁面函数,将标准 k-ε模型、RNGk-ε模型、Realizablek-ε模型和雷诺应力模型应用于半封闭狭缝湍流冲击射流的数值模拟,采用减小网格尺寸和提高差分格式精度等措施来减小数值伪扩散对冲击射流流动的影响。结果表明:雷诺应力模型和 Realizablek-ε湍流模型在湍流冲击射流的数值模拟中具有一定的优越性,Realizablek-ε模型的计算量较小;减小网格尺寸并不能降低数值黏性对计算结果的影响;提高差分格式的精度可以在一定程度上降低数值黏性对计算结果的影响,MUSCL格式并没有显著提高计算结果的精度。

射流;湍流模型;数值模拟;差分格式

海洋石油工程中,废弃的平台和裸露在海水中的井口、套管等设施对过往船舶的安全造成巨大影响,严重时会发生船毁人亡的恶性事件,因此必须予以拆除。目前,对废弃平台和套管的处理主要采用机械切割和炸药爆破的方法。机械切割效率较低,如切割 4层套管一般需 3～4 d,而炸药爆破过程中产生的冲击波会对周围海洋环境造成不良影响。为此,人们开始应用高压水射流切割技术。高压水射流依靠从孔口喷出的高速流体对被切割壁面的撞击作用实现切割,是一种典型的湍流冲击射流流动。有关冲击射流流动的研究文献报道已较多,其中包括试验和数值模拟等手段,但由于冲击壁面附近流线发生弯曲,流动的动力学特征复杂,对于该流动的模拟属于计算流体力学中的难题,因此较多文献中数值模拟与试验结果不能很好地符合。为了更好地模拟湍流冲击射流流动,研究人员在湍流模型的改进和控制方程差分格式的选取上作了许多研究工作,取得了很大进展[1-6]。笔者在前人研究的基础上,采用不同湍流模型,结合不同差分格式和不同网格尺寸对二维狭缝中湍流冲击射流流场进行数值模拟,并与试验结果进行对比,为工程实际应用提供理论依据。

1 物理模型及数值模拟

计算所用的物理模型如图 1所示。具有一定速度的流体从二维狭缝中喷出,冲击到无限大光滑平板上。狭缝出口附近安放了封闭板。狭缝宽度 b=0.01 m,上下平板间距8b,狭缝出口处雷诺数Re与试验条件相同,Re=10000(Re=ubb/ν,ub为狭缝出口截面上的平均速度,ν为空气的运动黏性系数)。考虑到物理模型的对称性,取流场的一半 8b×50b作为计算域。由于气体射流速度较低(马赫数M a≪1),假设流动定常且不可压缩。原点 o取在狭缝中轴线与冲击板的交点处,x轴和 y轴正方向示于图 1中。采用四边形网格对计算域进行划分,网格数量约为 43 000。压力 -速度耦合采用 SI MPLE算法进行求解,收敛判据为所有变量的残差绝对值小于 10-4。计算中采用的湍流模型有标准 k-ε模型、RNGk-ε模型、Realizablek-ε模型和雷诺应力模型。有关这些模型的控制方程形式可参见文献[7-9]。

本文中采用的差分格式有动量方程的迎风格式和 MUSCL(monotone upstream-centered schemes for conservation laws)格式[10],加密后的网格数约为 172 000。

图 1 狭缝湍流冲击射流的物理模型Fig.1 Physicalmodel of slot turbulent i mpinging jet

2 计算结果分析

2.1 湍流模型对计算结果的影响

本文中所选用的湍流模型都是在雷诺平均假设的基础上建立的,并且标准 k-ε模型、RNGk-ε模型和 Realizablek-ε模型又都是在 k-ε湍流模型的基础上发展的,适用于各向同性湍流。由于湍流冲击射流在壁面附近的流动为各向异性湍流流动,所以采用这些湍流模型从机制上就存在不足。但是,由于工程计算的精度要求比理论研究的要低,同时这些湍流模型的形式较简单并且计算量小,所以这些湍流模型在一些工程应用中仍在使用。雷诺应力模型是各向异性湍流模型,但是它的计算量非常大,收敛相当困难,其应用也因此受到影响。

图 2为不同湍流模型计算结果与试验数据[2]的对比。

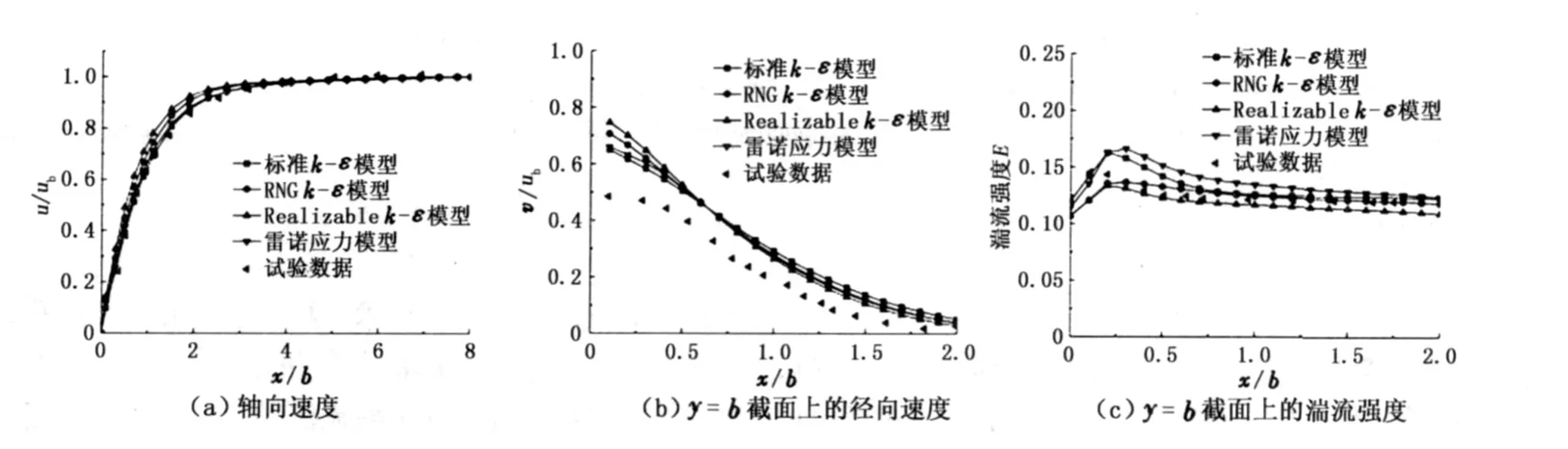
图 2 不同湍流模型计算结果与试验结果的比较Fig.2 Comparison of calculated results by different turbulence models and experi mental results

由图 2可知:轴线上轴向速度的预测中,标准 k -ε模型与雷诺应力模型的计算结果更接近于试验数据,RNGk-ε模型的次之,Realizablek-ε模型的最差;径向速度的预测中,4种湍流模型的计算结果与试验数据间存在较大的误差,靠近冲击壁面区域,标准 k-ε模型和雷诺应力模型的计算结果最接近试验数据,RNGk-ε模型次之,Realizablek-ε模型最差,离开冲击壁面一定距离后,Realizablekε模型的计算结果最接近试验数据,雷诺应力模型和 RNGk-ε模型的次之,标准 k-ε模型的最差;对湍流强度的预测中,Realizablek-ε模型的计算结果普遍低估了对应位置处的湍流强度,其他 3种模型则高估了对应位置处的湍流强度,Realizablek -ε模型和 RNGk-ε模型与试验数据最接近,标准k-ε模型的次之,雷诺应力模型的预测结果最差。4种湍流模型中,Realizablek-ε模型的计算量较大,但比雷诺应力模型的计算量要小很多,也就是说,在模拟湍流冲击射流时,基于各向异性的雷诺应力模型并不优越于 Realizablek-ε模型。

对于上述 4种模型:标准 k-ε模型中采用了常数形式的湍流普朗特数,因此该模型只适用于各向同性的高雷诺数湍流流场的计算;RNGk-ε模型通过引入考虑流动的不平衡应变率分量对湍动能耗散率方程源项中的系数进行了修正,并且为湍流普朗特数提供了解析方式,因此与标准 k-ε模型相比RNGk-ε模型的预测效果要好一些;Realizablekε模型中不仅提供了新的湍流黏度公式,而且从涡量波动的输运效应出发推导了严格意义上的湍动能耗散率方程,这使得该模型满足了雷诺应力的某些数学限制条件,而且与湍流流动的本质具有一致性。雷诺应力模型将注意力转移到雷诺应力分量的计算上,但由于目前的试验手段和认识深度而无法准确给出该模型的初始条件和边界条件,只能以时均量的方式给出,这就导致虽然该模型可以较清晰地反映出流场的各向异性,但在某些情况下计算结果与试验数据的吻合程度不优于各向同性湍流模型。

计算结果与试验数据间存在较大的误差,分析其原因,主要有以下几个方面:①试验测量工况参数与计算工况参数之间存在一定差别,狭缝入口处详细的速度分布和湍流参数测量困难,计算过程中入口处的湍流参数部分采用了经验公式确定,而湍流冲击射流的流动控制方程在数学上具有椭圆形性质,入口边界条件的变化对整个流场都会产生影响,从而导致预测结果与试验数据间误差的产生;②试验数据测量误差的影响,由于冲击壁面的反射作用,射流在壁面附近区域流线发生弯曲,滞止点附近的动力学特征非常复杂,这给试验测量带来了很大困难,导致近壁区测量结果的可重复性下降[3];③数值黏性的影响,计算中采用了四边形的结构化网格,在流线发生弯曲的近壁区,流线方向与网格界面的法线方向间存在一定角度,这造成界面插值过程中产生较大的截断误差,从而降低了预测结果的精度。

数值黏性主要来源于控制方程的离散过程,为了降低数值黏性对计算结果的影响,本文中尝试采用减小网格尺寸和提高差分格式精度两种方法。

2.2 网格尺寸对计算结果的影响

减小网格尺寸可以提高控制方程的离散精度。在原有计算网格的基础上,将网格尺寸减小 0.5倍,网格数目由原来的 43 000增加到 172 000。网格加密后,计算量增加,所需计算机内存激增。利用 Realizablek-ε模型对疏、密两种网格进行计算,计算结果见图 3。从两种网格下的计算结果看,加密后的计算结果与试验数据相比并无明显的改善。对轴向速度和径向速度的预测中,部分区域加密后的预测结果反而比加密前的要差。这说明改变网格尺寸并不能改善对湍流冲击射流的预测结果。

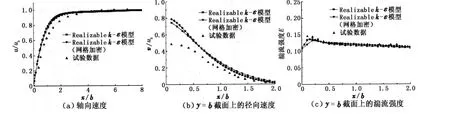
图 3 网格尺寸对计算结果的影响Fig.3 I nfluence of mesh density on numerical results

2.3 差分格式对计算结果的影响

上述计算过程中,控制方程对流项的差分格式为一阶精度的迎风格式,在计算湍流冲击射流中会导致较大的计算误差。为了实现对湍流冲击射流的精确求解,尝试采用具有三阶精度的MUSCL格式来离散动量方程中的对流项。采用 MUSCL格式后,模拟计算的工作量增加,程序收敛缓慢。计算结果与试验数据的比较如图 4所示。从对比结果可以看出,采用MUSCL格式后,部分计算结果与试验数据的符合程度要好于迎风格式的计算结果,但仍然存在较大差别。所以,采用MUSCL格式后对湍流冲击射流流动的模拟结果与迎风格式相比有一定的改进,但与试验数据间仍存在明显的定量误差。

图 4 差分格式对计算结果的影响Fig.4 I nfluence of difference scheme on numerical results

3 结 论

(1)雷诺应力模型和 Realizablek-ε湍流模型在湍流冲击射流的数值模拟上具有一定的优越性,同时 Realizablek-ε模型还具有计算量小的特点。

(2)减小网格尺寸并不能降低数值黏性对计算结果的影响。提高差分格式的精度可以在一定程度上降低数值黏性对计算结果的影响,MUSCL格式并没有显著提高计算结果的精度。

(3)要改善湍流冲击射流流动的预测结果,研究重点应放在对湍流模型中反映不平衡应变率参量的模化方面。

[1] CRAFT T J,GRAHAM L J W,LAUNDER B E.I mpinging jet studies for turbulence model assessment-Ⅱ:an examination of the performance of four turbulence models [J]. International Journal of Heat and Mass Transfer, 1993,36(10):2685-2697.

[2] YOSH I DA H,SUENAGA K,ECH IGO R.Turbulence structure and heat transfer of a two-dimensional impinging jet with gas-solid suspensions[J]. International Journal of Heat and Mass Transfer,1990,33(5):859-867.

[3] ASHFORTH-FROST S,JAMBUNATHAN K.Numerical prediction of semi-confined jet impingement and comparison with experimental data[J].International Journal for NumericalMethods in Fluids,1996,23:295-306.

[4] 陈庆光,徐忠,张永建.两种差分格式和两种湍流模型在轴对称冲击射流数值计算中的比较[J].空气动力学学报,2003,21(1):82-89.

CHEN Qing-guang,XU Zhong,ZHANG Yong-jian. Comparison of two different schemes and t wo turbulence models in the numerical computations of an axisymmetric impinging jet flow[J].ActaAerodynamica Sinica,2003, 21(1):82-89.

[5] 徐惊雷,徐忠,黄淑娟.用非线性 k-ε模型对狭缝冲击射流进行数值计算 [J].西安交通大学学报,1999, 33(8):106-107,110.

XU Jing-lei,XU Zhong,HUANG Shu-juan.Numerical study of slot impinging jet with nonlineark-εmodel [J].Journal of Xi´an JiaotongUniversity,1999,33(8): 106-107,110.

[6] 李根生,易灿,黄忠伟.自振空化射流改善油层渗透率机理及实验研究 [J].中国石油大学学报:自然科学版,2007,31(1):72-75.

L I Gen-sheng,YI Can,HUANG Zhong-wei.Mechanism and experimental study of self-resonating cavitating jet for improving polluted rock per meability[J].Journalof China University of Petroleum(Edition of Natural Science), 2007,31(1):72-75.

[7] LAUNDER B E,SPALD I NGD B.Lectures inmathematicalmodelsof turbulence[M].London:Academic Press, 1972.

[8] YAKHOTV,ORSZAG SA.Renormalization group analysisof turbulenceⅠ:basic theory[J].Journalof Scientific Computing,1986,1(1):1-51.

[9] SH IH T-H,L I OU W W,SHABB IR A.A newk-εeddy-viscosity model for high Reynolds number turbulent flows[J].Computers&Fluids,1995,24(3):227-238.

[10] van LEER Bram. Toward the ultimate conservative difference scheme:a second-order sequel to Godunov´s method[J].Journal of Computational Physics,1979, 32:101-136.

(编辑 李志芬)

Numerical si mulation of sem i-confined slot turbulent i mpinging jet using different turbulence models

WANGMing-bo,WANG Rui-he
(College of Petroleum Engineering in China University of Petroleum,Q ingdao266555,China)

In order to meet the need of abandoned platfor m cutting technology used in offshore petroleum engineering,different turbulence models including the standardk-εmodel,RNGk-εmodel,Realizablek-εmodel and Reynolds stress modelwere used to simulate the semi-confined slot turbulent impinging jet.In order to reduce the influence of numerical diffusion on the computational results,measures such as decreasing the mesh size and increasing the precision of difference scheme were used.The results show that the Reynolds stressmodel and the Realizablek-εturbulence modelperfor m better than other two models.Decreasing the mesh size does not reduce the effect of numerical viscosity on computational results, and increasing the precision of difference scheme can reduce the effect of numerical viscosity on computational results at certain degree.And the Realizablek-εturbulence model in conjunction withMUSCL scheme shows a little better perfor mance than othermodels.

jets;turbulence model;numerical simulation;difference scheme

TG 156

A

10.3969/j.issn.1673-5005.2010.04.014

1673-5005(2010)04-0075-04

2010-02-26

国家自然科学基金项目(50574062);国家高技术研究发展计划项目(2006AA06Z218)

王明波(1979-),男(汉族),山东荣成人,讲师,博士,主要从事冲击射流和液固两相流动研究。