基于序贯指示模拟的信息预测方法

杜 奕，周雪萍，李远刚

基于序贯指示模拟的信息预测方法

杜 奕1，周雪萍2，李远刚3

（1. 上海第二工业大学计算机与信息学院，上海 201209；2. 新疆油田公司采气一厂，克拉玛依 834000；3. 新疆油田公司采油二厂，克拉玛依 834000）

信息预测在医药、地质、军事等众多工程应用领域中发挥着重要作用。在模拟过程中仅利用少量的已知数据预测未知信息非常困难。为了获得更好的模拟效果，在估计或预测未知区域的过程中采用内插和外插的方法。作为一种非参数的估计算法，指示克里格方法虽然能够在给定周围条件数据的情况下估计任何位置的条件累积分布函数，但并不能保证结果分布的有效性。序贯指示模拟(Sequential indicator simulation, SISIM)综合了指示克里格方法和序贯方法在模拟非参数连续和离散分布函数上各自的优点。该方法根据一系列自定义阈值确定非参数累积分布函数，模拟过程中利用底部和顶部外插函数给出分布函数的形状。实验结果表明模拟结果具有与真实数据相似的分布特征，证明了该方法的实用性。

插值；指示克立格；序贯指示模拟；外插法；信息预测

0 引言

未知区域的信息预测在很多科学领域发挥着非常重要的作用。例如，在医药、军事、地质、气象和矿业等领域，信息预测技术被广泛应用。在预测未知信息的过程中，插值方法可以利用一些离散点来估计未采样点的未知属性，从而根据一些数学、物理等规则建立正确完整的数学模型。尽管目前已经提出了大量的插值方法，但精确的信息模拟和预测仍然难以实现。插值方法主要分为两类：“确定性”方法和“不确定性”方法。这里的“确定性”是指插值函数的形式、参数和结果总是确定的。“确定性”方法包括距离反比加权法、基于三角网格的方法以及基函数法等。“不确定性”插值方法的“不确定”性，一方面表现在插值形式的随机性上，另一方面表现在插值参数的选取和确定需要依赖于概率统计原则[1-2]。不确定性插值方法主要包括地质统计学领域的各种克里格方法和随机模拟方法。基于变差函数的克里格方法和随机模拟方法都属于两点地质统计法[3-4]，它们仅描述空间两点间的关系，难以重构如曲线形状这样的复杂图形。

不确定性方法一般分为两类[5]。一类是生成唯一插值结果的插值方法。这种插值方法通常作为低通过滤器用来平滑模拟变量空间中可变的局部细节。该方法提供一种不确定性的测量手段，如克里格方差。第二类不确定性方法是随机模拟方法，可以生成多种可能的空间分布结果。这些随机算法属于典型的全通过滤器，能够再现空间可变性的所有范围。多种随机结果之间的波动可以对结果中隐含的不确定性特征进行可视的定量测量。

指示克里格是一种非参数估计算法，该方法在给定条件数据的前提下可以估计任意位置上条件累积分布函数(conditional cumulative distribution function, ccdf)。该方法适用于连续型和离散型变量的信息预测。指示克里格方法将输入的数据转换成二进制的指示数据，然后对这些转换过的指示数据应用简单或普通克里格方法。对于连续型变量，通过克里格方法对在阈值以下的概率确定条件累积概率函数。对于离散型变量，可以估计属于某一特定分类的概率分布[4]。

序贯指示模拟(SISIM)将指示克里格方法和序贯方法相结合，实现了非参数的连续型与离散型的分布模拟。根据连续型序贯指示模拟(SISIM)的理论，本文提出了一种利用外插方法的连续型序贯指示模拟的信息预测方法，实现结果验证了该方法的实用性与有效性。

1 概念与方法

1.1序贯模拟

序贯模拟的基本思想是：某一位置u邻域内的所有已知数据(原始数据和已模拟的数据)都可作为条件数据，在这一前提下进行模拟。考虑N个随机变量Zi的联合分布。Zi可以代表：

● 某一区域内离散在N个网格节点上的同一属性；

● 同一点处的N个不同属性；

● N’个节点上的K个属性的联合分布，N =KN’。

这N个随机变量的n个数据，其相应的N元的条件累积分布函数ccdf则可表示成：

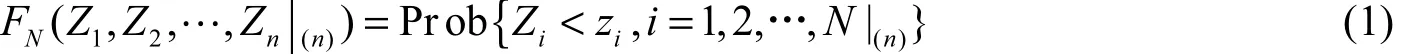
这里Zi是第i个属性值，FN(·)是条件概率分布函数(ccdf)。为了得到一个来自(1)式的N元样本，可以由N个相继的步骤来完成。每一步都是ccdf中的一个抽样，这样先前已模拟的数据可作为下一个抽样的条件数据，条件数据不断增加，已知信息集由(n)更新为(n+1)，序次考虑所有N个随机变量，重复上述过程。

1.2克里格

克里格在本质上是一种广义线性退化算法，它可以在最小方差情况下提供最优估计值。该估计值是由硬数据的线性组合实现的[5-7]，计算公式表示如下：

式(2)中的z*(u)是信息预测估计值。z(u)表示待预测区域A的硬数据(主要信息)，uA∈是位置向量。z(uα)(α = 1,2, …, n)是位于uα位置的第α个信息采样数据。n是区域A中的采样数据点数目。权值λα由克里格方程获得，uα与u之间的关系式如下：

式(3)中的h是描述uα与u之间距离关系的向量。实际上，式(3)要受限于uα与u之间的关系，例如两者的变差函数和协方差。

1.3指示克里格

指示克里格方法可以应用于离散与连续型变量。但是，对于连续型变量，指示克里格方法不能保证概率的单调增长，也无法保证连续性变量的取值在0和1之间[4]。

连续型指示变量的定义如下：

式(4)中z(u)为待模拟的变量，zk(k = 1, …, K)为阈值。

对于任意阈值zk，指示克里格可以在已知n个数据的条件下估计条件累积概率函数。公式(5)给出了条件累积概率函数的定义：

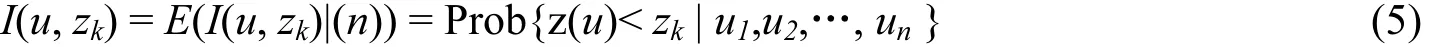
由公式(5)可知，根据不同的阈值zk, k = 1, …, K，可以计算生成不同的条件累积概率函数I(u, zk)。

对于指示克里格，实验变差函数γI∗(h,z)定义为

式(6)中N(h)为所有变差函数的数目。本文仅讨论连续型SISIM，不涉及离散型指示克里格方法。

1.4 SISIM

在连续型SISIM过程中，可以沿着模拟路径的每个位置，对于每个阈值利用基于指示条件数据的指示克里格方法估计ccdf值[4,8]。

SISIM模拟过程中不需要任何高斯假设。在连续型SISIM过程中，通过估计不超过已限定阈值集的概率计算生成ccdf。给定的阈值越多，对应的条件累积概率函数越精确。SISIM模拟过程如下[4]：

步骤1 确定阈值：z1, z2,…, zK；

步骤2 定义一条随机模拟路径；

步骤3 在模拟路径的每个位置u上，寻找其周围的条件数据z(u1), z(u2) ,…, z(un)，将每个数据z(uα) (α = 1,2,…, n)转换为指示值表示的向量；

步骤4 对于K个阈值，根据克里格法估计每个阈值对应的指示随机向量I(u, zk)，I(u, zk) = Prob{z(u)＜ zk| z(u1), z(u2),…, z(un) }，估算对应于变量z(u)的条件累积概率函数Fz(u)；

步骤5 从上述条件累积概率函数中抽取一个值，将其作为位置u上的数据值；

步骤6 重复步骤3至步骤5直到模拟完所有位置。

条件累积概率函数Fz(u)的定义如下：

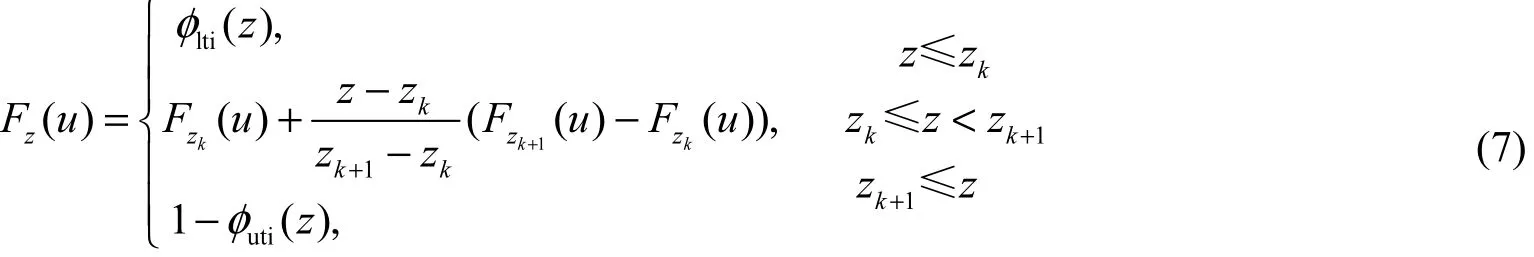
式(7)中Fzk(u)根据指示克里格法计算获得。φlti(z) 和 φuti(z)分别为上，下尾外推(the lower and upper tail extrapolation)。

1.5 上下尾外推

非参数条件累积概率函数F(u)根据一系列阈值z1, z2…, zK进行定义，并以相同的增量1/(K + 1)实现递增，如F(z1) = 1/(K + 1)， 而F(zK) = K/(K+1)。如果z1和zK不是最小和最大值，则需要对分布函数F(u)的尾部进行建模。如果z1和 zK分别为最小和最大值则不需要进行任何外推估计。下尾外推函数提供了最小值zmin和第一个值z1的分布形状[4,9]。

下尾外推函数如下定义[4,10]：

(1) Z被限定：F(zmin) = 0。F的下尾外推函数为

式(8)中的1ω≥用于调节上述函数的增加或减少。如果1ω=, 那么zmin和 z1之间的所有值均相等。

(2) Z不被限定：F的下尾外推函数为

式(9)中的exp为指数函数。

上尾外推函数如下定义：

(1) Z被限定：F(zmin) =1。上尾外推函数为

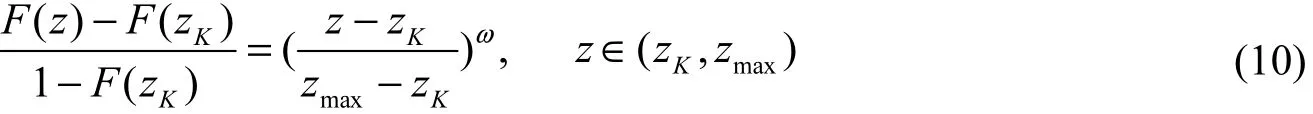
式(10)中的01ω≤≤用于调节上述函数的增加或减少。如果1ω=, 那么zmax和 zK之间的所有值均相等。

(2) Z不被限定：F的上尾外推函数为

式(10)中的1ω≥.

2 实验结果和分析

实验所用的二维样本数据为实际测得的某区域的真实海拨值。该数据集为包含10 000个数据点的点集网格，用于测试评价SISIM的模拟效果。用于条件数据的样本数据如图1所示。背景设为黑色用于突出显示样本数据。工具条中的不同颜色表示区域中已知数据的不同取值。可以看出仅有少量结点为已知数据。

图1 样本数据Fig.1 Sample data

图1 中的样本数据是从图2所示的真实海拨数据中抽样获得。因此可以通过对比模拟结果和图2的相似性来评估本文算法的有效性。相似度越高，则说明方法越有效。原始图像数据的直方图如图3所示。

图2 原始图像数据Fig.2 Original data

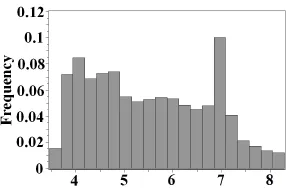
图3 原始图像数据的直方图Fig.3 Histogram of original data

下面给出了本文方法的实验结果。两个利用SISIM和样本数据生成的随机模拟结果分别如图4(a)和(b)所示。结果显示模拟结果和原始图像数据的结构特征非常相似。

图4 使用SISIM和样本数据获得的模拟结果. (a)结果1 (b)结果2Fig.4 Simulated results using SISIM and sample data. (a) result 1; (b) result 2.

上述两个模拟结果的直方图分别如图5(a)和5(b)所示。可以看出模拟结果和原始图像数据直方图中的数值分布非常相似，证明本文方法有效。

图5 序贯指示模拟结果的直方图 (a)结果1;(b)结果2Fig.5 The histograms of simulated results using SISIM and sample data. (a) result 1; (b) result 2

表1给出了模拟结果与初始图像数据的平均值及方差值，不难看出模拟结果与初始数据的平均值和方差值也都非常接近。

表1 初始数据和模拟结果的平均值和方差值Tab.1 The average and variance of original data and simulated results

3 结束语

基于序贯指示模拟的信息预测方法可以有效实现未知信息的预测。本文讨论了连续型的序贯指示模拟方法。在不需要任何高斯假设的前提下，SISIM将指示条件数据和序贯模拟相结合实现每个待模拟结点上未知数据的有效预测。模拟过程中使用了指示克里格和外推法用于计算上下尾部函数。由实验结果可以看出，模拟结果与初始数据非常相似，从而证明了本文方法的实用性。

[1] ZHANG T , LU D T , LI D L . Porous media reconstruction using a cross-section image and multiple-point geostatistics[C]// Proceedings of ICACC, 2009, Singapore, 2009:24-29.

[2] ZHANG T, LU D T, LI D L . A statistical information reconstruction method of images based on multiple-point geostatistics integrating soft data with hard data[C]//Proceedings of ISCSCT 2008. Shanghai, China, 2008:573-578.

[3] LU D T, ZHANG T, YANG J Q , LI D L , KONG X Y. A reconstruction method of porous media integrating soft data with hard data[J]. Chinese Science Bulletin, 2009, 54(11): 1876-1885.

[4] RENY N, BOUCHER A, WU J B. Applied Geostatistics with SGeMS: A Users’ Guide[M]. Cambridge: Cambridge University Press, 2009:108-134.

[5] ZHANG T, DU Y. The study of cokriging using a Markov model[C]// Proceedings of ICETC 2010. Shanghai, China, 2010:6-11.

[6] ZHANG T, DU Y. A novel interpolation method using a Markov model and COSGSIM[C]// Proceedings of ICCAE 2010. Singapore, 2010: 691-695.

[7] ZHANG T, DU Y. A novel method for information prediction[C]//Proceedings of ICSAP 2010. Bangalore, India, 2010:3-7.

[8] MA X L, JOURNEL A G. An expanded GSLIB cokriging program allowing for two Markov models[J]. Computers & Geosciences, 1999, 25: 627-639.

[9]GOOVAERT SP. Geostatistics for Natural Resources Evaluation[M]. New York: Oxford University Press. 1997: 54-80.

[10] ALMEIDA A, JOURNEL A G. Joint simulation of multiple variables with a Markov-type coregionalization model[J]. Mathematical Geology, 1994, 26(5): 565-588.

An Information Prediction Method Using SISIM

DU Yi1, ZHOU Xue-ping2, LI Yuan-gang3
(1. School of Computer and Information, Shanghai Second Polytechnic University, Shanghai 201209, P. R. China; 2. NO.1 gas production plant of Xinjiang oilfield company, Karamay 834000, P. R. China; 3. NO.2 oil production plant of Xinjiang oilfield company, Karamay 834000, P. R. China）

Information prediction plays an important role in many fields such as medical, geological and military fields. However, it is quite difficult to predict the unknown information only by some sparse known data in the process of simulation. Therefore, some interpolation or extrapolation methods are used to estimate or predict the unknown region for better simulated results. Indicator kriging is a non-parametric estimation algorithm used to estimate the conditional cumulative distribution function at any location given neighboring conditioning data, which cannot guarantee that the resulting distributions are valid. Sequential indicator simulation (SISIM) combines the indicator kriging with the sequential method to simulate non-parametric continuous or categorical distributions. In SISIM, a non-parametric cumulative distribution function is determined from a set of threshold values. The lower tail extrapolation function and the upper tail extrapolation function provide the shapes of the distribution functions during the simulation of SISIM. Experimental results show that the simulated results have the similar characteristics of distributed values with the original one, demonstrating that the proposed method is practical.

interpolation; indicator kriging; SISIM; extrapolation; information prediction

TP391

A

1001-4543(2010)04-0285-06

2010-09-15;

2010-10-28

杜奕（1977－），女，江苏吴江人，副教授，博士，主要研究方向为数据分析与处理，电子邮件：duyi@it.sspu.cn