Lingo软件在数学建模竞赛中的应用
金晶晶
(福建交通职业技术学院基础部,福建福州350007)
Lingo软件在数学建模竞赛中的应用
金晶晶
(福建交通职业技术学院基础部,福建福州350007)
针对三道全国大学生数学建模竞赛赛题,利用Lingo软件对模型进行求解,并分析了Lingo软件在求解较大规模数学规划模型所发挥的作用。
Lingo软件;数学建模;数学规划;曲线拟合
数学建模(Mathematical Modeling)是对现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,作出一些必要的简化假设,运用适当的数学工具,得到一个数学结构的过程[1]。
Lingo是Linear Interactive and General Optimizer的缩写。Lingo软件是美国芝加哥大学的Linus Schrage教授于1980年前后开发出来的一套专门用于求解最优化问题的软件包,即“交互式的线性和通用优化求解器”,包括功能强大的建模语言,建立和编辑问题的全功能环境,读取和写入Excel和数据库的功能,以及一系列完全内置的求解程序。使用者甚至不需要指定或启动特定的求解器,因为Lingo会读取方程式并自动选择合适的求解器。目前Lingo产品已经有Lingo8.0版本,新版本的求解规模都在原有基础上得到进一步加强。Lingo软件的最大特色在于其具有的快速建构模型、轻松编辑数据、强大求解工具、交互式模型或建立完成应用、丰富的文件支持。纵观近几年全国大学生数学建模竞赛赛题,参赛者大都需要处理较复杂的数学规划和曲线拟合等问题,模型的建立与求解较为复杂、计算量大,而matlab、mathmatica等软件语法比较复杂不易掌握。Lingo软件程序简洁、计算精度高、结果可靠、易于修改和扩展,其内部建模语言是建立与求解大规模数学规划模型的有力武器。2000年全国大学生数学建模竞赛B题(钢管订购和运输)中的最小费用流问题、2004年全国大学生数学建模竞赛C题(酒后驾车)的曲线拟合问题、2006年全国大学生数学建模竞赛中C题(易拉罐的最优设计)的非线性规划问题都可以充分展示用Lingo建模语言求解的优越性。
1 非线性规划模型
历年全国大学生数学建模竞赛都需解决最优生产计划、最优分配最优设计、最优决策、最佳管理等较为复杂的非线性规划问题,模型由决策变量、目标函数、约束条件三个要素组成,其计算量较大,可用Lingo软件求解。
2006“高教社杯”全国大学生数学建模竞赛C题[3]第二小题,设易拉罐是一个正圆柱体,什么是它的最优设计?经测量得圆柱的上底厚度为a=0.036cm、下底厚度为c=0.040cm、圆柱侧壁厚度为b=0.012 cm。考虑易拉罐设计美观性、便于把握以及材料节省等因素,于是建立目标规划模型如下:利用Lingo8.0编程如下:



Lingo以语句Model开始,以语句End结束,这两个语句单独成一行。语句分为集合定义部分、数据初始化部分、目标函数、约束条件部分,这几个部分的先后次序无关紧要。min开头的语句表示求目标函数最小值。“!”开头的语句是注释语句,Lingo不作运行,每条中间语句必须以“;”号作为结尾。注意乘号不能省略,语句不计大小写。
运行SOVLE,得部分结果如下:
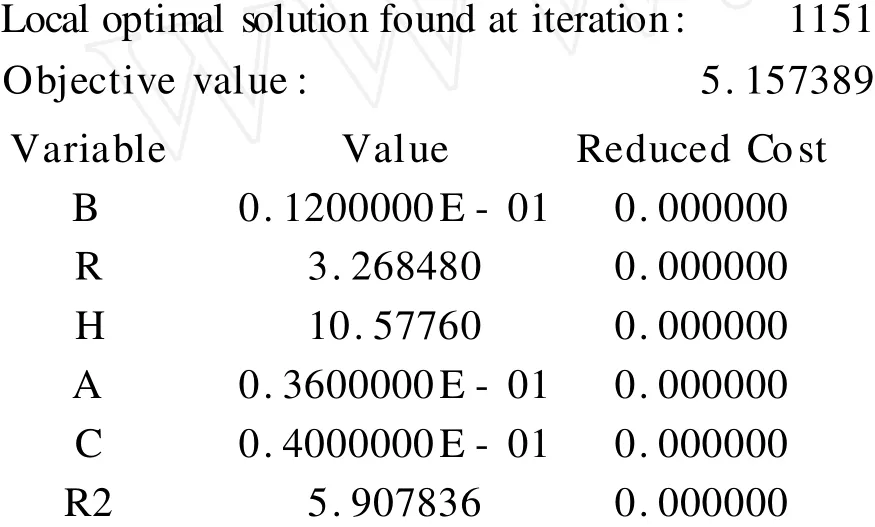
即底面半径为3.268480,圆柱体高为10.57760时,用料体积为5.157389,此为最优设计。第三题亦可按此方法迎刃而解。上例充分体现Lingo其简单易学、方便快捷的优越性。
2 曲线拟合模型
曲线拟合在众多领域中得到了广泛的应用,将曲线拟合问题转化为数学规划模型,并使用Lingo软件来求解,该方法简便快捷,是实现曲线拟合的一个有效方法。
2004年全国大学生数学建模竞赛C题(酒后驾车)中给出某人短时间内喝下两瓶啤酒后,间隔一定时间得到数据。以下建立无约束的非线性规划模型[2]。间隔一定时间t测量他的血液中酒精含量y (毫克/百毫升),得到数据如表1:
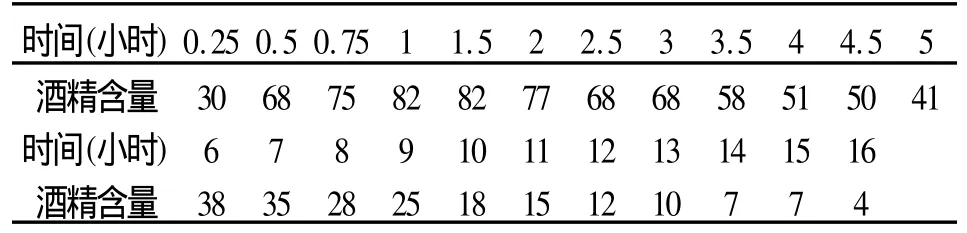
表1 2004年全国大学生数学建模竞赛C题(酒后驾车)数据
题目要求结合给定数据建立饮酒后血液中酒精浓度的数学模型。通过建立微分方程模型得到短时间内喝酒后血液中酒精浓度与时间的关系为:

求均方误差

取极小值的待定系数,即为最小二乘解。下面用Lingo软件求解,具体算法如下:

以上程序中,SETS和ENDSETS之间的语句是对集合作定义,在此所定义的BAC是包含23个成员的集合,T和Y是BAC的两个属性,分别表示时间t和血液中酒精浓度y,它们都是含有23个成员的一维数组。DATA和ENDDATA之间的语句是对T和Y的进行赋值,其中@SUM和@EXP是Lingo提供的内部函数,@SUM的作用是对某个集合的所有成员求某个表达式的和,该函数需要两个参数,第一个参数为集合名称,指定对该集合的所有成员求和,此处第一个参数是BAC,它有23个成员,则求和运算对这23个成员进行。第二个参数是一个表达式,表示求和运算对该表达式进行,两个参数之间用“:”号隔开。如果有约束条件,可放在目标函数之后,此处没有约束条件,故目标函数之后即以END结束整个程序。点击SOLVE,运行结果如下:

LINGO求多元函数极小值时内部所采用的算法效率高、速度快、精度高。用于非线性曲线拟合时,对拟合函数的形式无任何限制,无需初始值,能准确地得到回归系数的最小二乘解,计算精度高,程序简洁。
3 最小费用流模型
运筹学的交通运输问题中,往往要求在完成运输任务的前提下,寻求一个使总运输费用最省的运输方案,这就是最小费用流问题。如果只考虑单位货物的运输费用,那么这个问题就变成最短路问题。模型的传统求解迭代次数太多,比较复杂,而matlab、mathmatica等软件语法复杂不易编程,Lingo8.0其内部语言为解决该类问题的强有力武器。
2000年全国大学生数学建模竞赛B题“钢管的订购和运输”是一道离散优化问题。如图1,有7家钢管生产厂Si(i=1,2,…7),提供钢管到一条拟铺设钢管的天然气输送主管道上的15个站点 Aj(j=1,2,…15)。钢管可通过公路和铁路运至铺设地点,图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原有公路,或者建有施工公路),空心圆点表示火车站。钢管运到站点后由各站点沿管道向两边铺设直至合拢。该题要求制定钢管订购和运输的优化计划,使总费用最小。

图1 天然气输送主管道图
欲解决该问题首先需确定从Si至Aj的最优路径,从而确定出钢管从i地运往j地的最小运费,即求解最小费用流问题。根据该题的需要,不妨设从Si至Aj的钢管经过铁路后,一旦走公路,则不会再通过铁路运输。下以S2为例,计算S2至Aj的最优路径。图1中Bk/Lk(k=16,2,…,32)中表示S2至沿铁路至火车站Bk的费用为Lk。问题转化为求以Si为起点、Aj为终点的赋权图的最短路径问题。由Dijkstra算法,运用Lingo8.0编程如下:


以上SETS开始至ENDSETS结束的内容是定义所有的边。“CITIES/1..33/:F;”是用集合CITIES定义一维变量 F,其格式为:“setname/memberlist(or1.. n)/:attribute,...”,一个集合只需要给出维数(mem-berlist,用1..n表示或其他文字符号表示或用集合表示),后接具有该维数的变量(attribute)。以上DATA开始至ENDDATA结束的内容是赋以上各边以相应的权。Dijkstra算法的循环语句为:“@FOR(CITIES( i)|i#LT# @SIZE(CITIES):F(i)= @MIN( ROADS(i,j):D(i,j)+F(j)));”,其中逻辑运算符“#LT#”表示小于。

即可求得单位钢管从S2到Aj的最小运费F(j) (j=1,…,15)如下:

表2 单位钢管从S2到Aj的最小运费
同理可求得S1,S3,S4,S5,S7,S7各点到目的点的最优单位运费。
经定量分析可得较合理的方案为:S1,S2,S3负责往铺设点A1至A9供应钢管,S4、S5、S6、S7负责往A8至 A15供应钢管。
Lingo软件内置建模语言以较少的语句、直观的方式描述较大规模的数学规划模型。其中,@ SUM、@For和@IF等语句的应用,极大地方便了数学模型的建立。此外,由曲线拟合模型可得,可以将原先不属于优化问题的模型,利用Lingo软件内部建模语言进行求解,较之传统的求解方法更简单。
在实际应用领域,Lingo其线性、非线性和整数规划求解程序已经被全世界数千万的公司用来做最大化利润和最小化成本的分析。Lingo能在产品分销、成分混合、生产与个人事务安排、存货管理、生产线性规划、运输、财务金融、投资分配、资本预算、混合排程、库存管理、资源配置等问题的数学建模中发挥巨大作用。
[1]姜启源,谢金星,叶 俊.数学模型:第三版[M].北京:高等教育出版社,2003:3-4.
[2]袁新生,廖大庆.用Lingo6.0求解大型数学规划[J].工科数学,2001(5):73-77.
Application of Lingo Software to Mathematical Contest in Modeling
J IN Jing-jing
(Basic Courses Dept.,Fujian Communication Technology College,Fuzhou 350007,China)
On the analysis of three questions in National Mathematical Contest in Modeling for College students,this paper puts forward the way in solving the model by using Lingo software accordingly,and analyzes the role the Lingo software plays in solving large-scale mathematical optimization model.
Lingo software;mathematical modeling;mathematical optimization;curve fitting
book=85,ebook=160
O141.4
A
1008-4738(2010)04-0085-04
2010-06-20
福建交通职业技术学院科技发展基金(Ky1001)。
金晶晶(1983-),男,福建交通职业技术学院基础部助教,理学硕士,研究方向:组合数学与图论。

