相邻亮、暗孤子相互作用的比较

李淑青，王爱国，冯中营，任全年

（太原工业学院理学系，山西太原 030008）

相邻亮、暗孤子相互作用的比较

李淑青，王爱国，冯中营，任全年

（太原工业学院理学系，山西太原 030008）

通过与亮孤子进行比较，分析了暗孤子的基本方程，求出了它的一个精确解，分析比较了相邻暗孤子间的相互作用，并对有平面波背景的暗孤子作了积分处理.

非线性方程 暗孤子解 相互作用 积分

1 暗孤子传输的基本方程

考虑在光纤媒介中传播的单频标量电场E,满足麦克斯韦方程,其解可表示为下面的形式

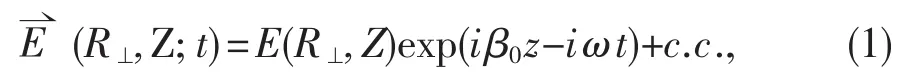
其中c.c指复共轭,ω是源频率,β0＝k0n0＝2kn0／λ是平面波演化常数.E(R⊥,Z)描述波包,不考虑非线性效应和衍射效应时,它是一个常数.如果把方程(1)代入到三维的标量波方程中,可以得到一般非线性方程

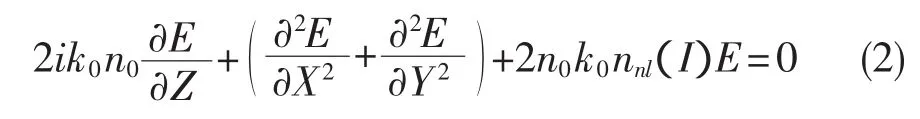
这里的非线性通过函数nnl（I）来体现.对于非线性克尔效应有nnl（I）＝n2I，n2是光媒介所具有的克尔效应的系数.现在引进无量纲坐标,可以得到 (2+1)维非线性薛定谔方程，取如下标准形式

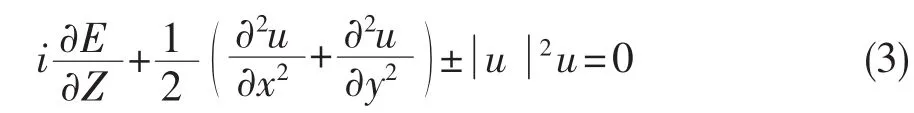
这里的符号(±)由非线性类型所定义(自散焦和自聚焦).

对于在实波导中传播的光脉冲,在某方向的场结构,如y方向,由波导的线性模式决定.麦克斯韦方程的解可写成

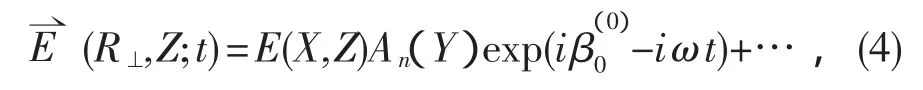
这里函数An（Y）描述相应的厚波导基本模.同时,把解代入到麦克斯韦方程中并且对Y进行平均化处理,便可得到标准的非线性薛定谔方程(NLS)[1]

2 非线性薛定谔方程的精确暗孤子解

人们已经从不同的角度分析了高阶非线性薛定谔方程,并在平衡了群速度色散、自相位调制、三阶色散和自陡效应后求出了类孤子解[2].含有自频移的高阶非线性薛定谔方程的类孤子解也有人求出并进行了稳定性分析[3-6].但是,类暗孤子解的相互作用自今研究者不多.在此通过逆解法求出了非线性薛定谔方程的一种暗孤子.

讨论暗孤子在光纤中的物理特性,首先讨论描述复电场波包的动力学方程[1]

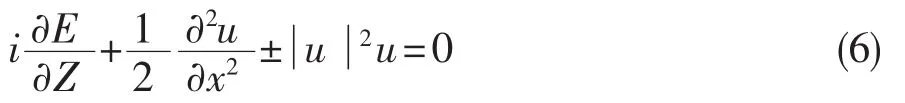
这里的 σ＝±1是k（ω）二阶导数的符号,对应于不同的光纤群速度色散类型,即σ＝－1时,代表反常色散, σ＝＋1代表正常色散.u代表电场波包的归一化振幅,z是沿着光纤的归一化距离.采用和亮孤子一样的归一化单位z→z／Z0，x＝（t－z／Vg）／tc，时间坐标t是延迟时间,它是在参考坐标中测量,并且参考坐标沿着光纤以群速度移动.

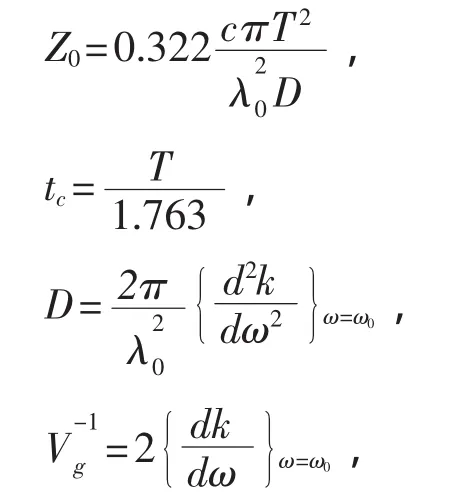
这里的T指脉冲宽度(FWHM).

非线性薛定谔方程(6)是一个可积系统,在非零边界条件下可以用逆散射方法求解.在这里我们假设解的形式为

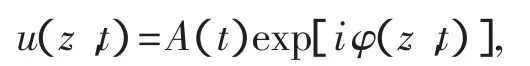
其中A（t）和φ（z，t）分别表示脉冲的振幅和相位.将该解代入方程(1)即可得到A（t）和φ（z，t）所满足的常微分方程,然后通过求解常微分方程则可得到暗孤子解.与亮孤子的主要区别是当→∞时,A（t）趋于一个非零常数.其通解可以写成

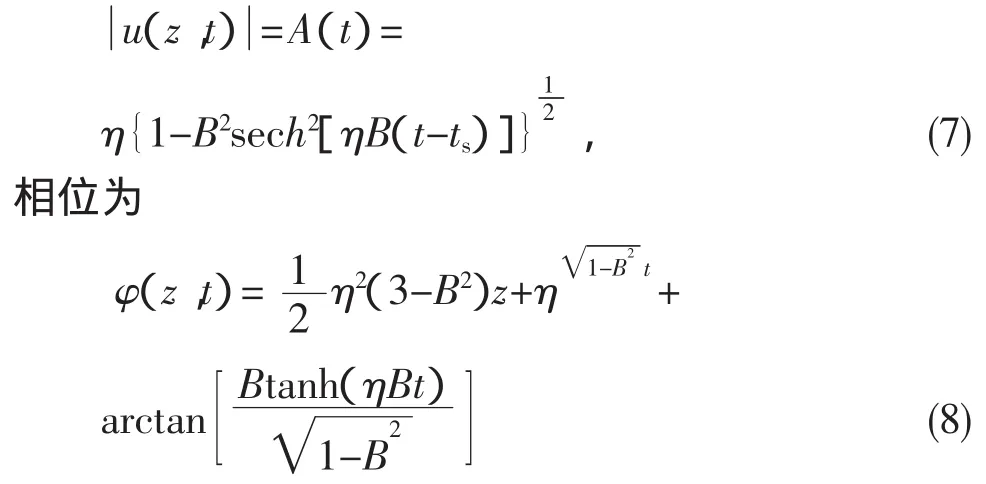
参量η和ts分别代表孤子的振幅和下陷位置.与亮孤子类似,选取ts＝0,不同的是暗孤子有一个新的参量B.物理上把＜1时的暗孤子称为灰孤子,以强调这一特征.参量B决定这种灰孤子的黑度,把B＝1时的暗孤子称为黑孤子.

3 数值研究相邻亮、暗孤子间的相互作用

在光孤子通信中,相邻孤子间的相互作用特点决定孤子传输的稳定性,决定传输的比特率,对于亮孤子,取初始脉冲的形式为

其中2q0描述相邻孤子间的距离.图1(a)(b)(c)分别是q0＝5.5,q0＝3.5和q0＝2.5的相邻孤子的演化情况,从图中可以看出相邻孤子相互作用平衡的最短距离2q0＝11,随着孤子间距的减小呈现出周期性的离合现象,并且距离越小离合周期越小.而对于暗孤子之间的相互作用.针对方程(6)取初始脉冲为

图2(a)(b)(c)分别是q0＝3.5,q0＝2.5和q0＝2.0的相邻孤子的演化情况,对比图1和图2可以看出,同样是q0＝3.5的情况,演化相同的距离后,亮孤子已有明显的相互作用现象而暗孤子还不明显,这说明暗孤子的相互作用较亮孤子的相互作用弱,而且随着两孤子间距的减小,相邻孤子间的相互作用与亮孤子间的相互作用也不相同,暗孤子表现为相互排斥,没有周期性离合,这为利用暗孤子作为光纤通信中的信息载体提供了可能.

图1 相邻亮孤子间的相互作用

图2 相邻暗孤子间的相互作用

4 暗孤子的积分处理

亮、暗孤子的区别也可以从积分中看出,亮孤子是没有边界的,而暗孤子有边界,它们的积分行为有很大的区别.实际上,只要选取合适的拉氏密度,方程(6)等价于欧拉方程,现在我们选取拉氏密度为如下形式

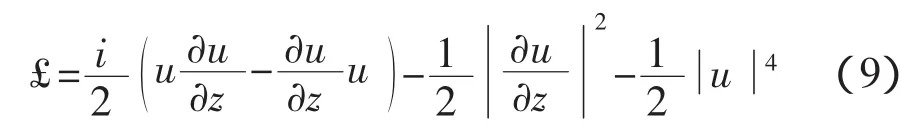
相应的哈密顿量就很容易求出

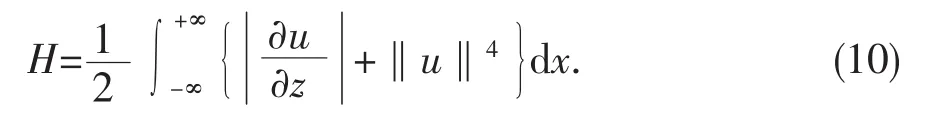
由于方程(6)是精确可积的,所以解的积分也是有限的.然而为了研究普遍情况下所存在的不变量,必须研究不可积的薛定谔模型.由于薛定谔方程描述的系统是保守的,由(10)所定义的总能量也是守恒的.另外,我们也考虑了场动量

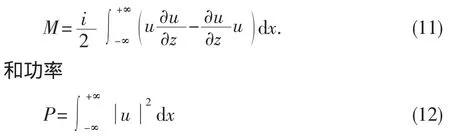
形式上看,方程(10)(11)和(12)适合于任何类型的边界条件.但对于非零边界条件,由方程(10)(11)和(12)所计算出的值是奇异的.

显而易见,对于具有非零边界条件的暗孤子也会出现同样的问题.因此必须对它们进行从新归一化.现考虑最一般的形式,暗孤子在平面波背景下的演化.方程(5)就是描述暗孤子在平面波背景下的演化,他的解可以写成下面的形式

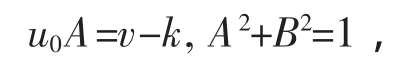
在这种形式中,暗孤子解由三个独立的参数决定,其中两个u0和k表示平面波背景的振幅和波数,只有A描述暗孤子本身,解(13)的渐进行为和平面波解是一致的.然而当x→±∞时,暗孤子具有不同的相位,他们的相对相位变化是

从新归一化暗孤子的积分形式,从方程 (10)(11)和(12)的积分形式可以很明显看出暗孤子实际上是一类前后沿为有限值而中心下限的“暗”脉冲,也可以看成是“平面波背景+暗孤子”.为了消除平面波背景,我们必须修改积分形式,使方程(13)的积分的变得有限可积.为了简化,我们取k=0,计算功率的方程(12)应该用总功率和相应平面波总功率的差去代替表示为

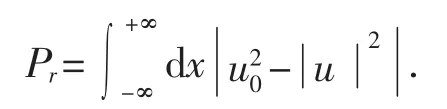
这样计算出由方程(13)所计算出的功率为,Pr＝2u0B重新归一化能量为

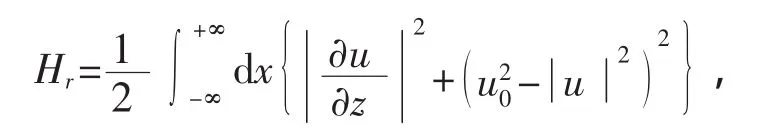
并且可以计算出,方程(13)所对应的能量为

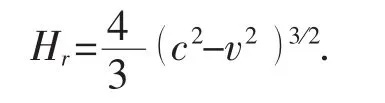
重新归一化的动量为

这里的△θ由方程(14)定义,把解(13)代入到方程动量表达式中,并令k＝0,可求出

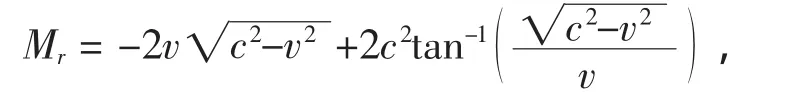
这里c2＝u20.因此对于一般非线性薛定谔方程的,暗孤子积分形式也要作如下处理:

这些值都是有限的.

总之,本文简单介绍了光脉冲在单模光纤中传输的基本演化方程-非线性薛定谔方程.采用逆解法求出了暗孤子的一种精确解,通过数值模拟分析比较了相邻暗孤子间的相互作用,深刻理解了它的调制不稳定性,并对有平面波背景的暗孤子作了积分处理.

[1]Hasegawa A,Tappert F.Transmission of stationary nonlinear optical pulses in dispersion dielectric fibers.1.Anomalous dispersion [J].Am Phys Lett,1973,23:142-144.

[2]Hasegawa A,Kodama Y.Solitons in Optical Communications[M].Oxford：Oxford U Press,UK,1995:1-56.

[3]Li Zhonghao,Lu Li.Chired Femtosecond Solitonlike Laser Pulse Form with Self-Frequency Shift[J].Am Phys Rev Lett,2003,89: 263901-03.

[4]李淑青,李录,李仲豪.考虑自频移的啁啾超短脉冲间相互作用的数值研究[J].光子学报,2004,33(4):862-864.

[5]Li Shuqing,Lu Li,Li Zhonghao.The properties of soliton solution on cw background in optical Fiberwith higher-order effects[J]. America Opt Soc Am B,2004,21:2089-2094.

[6]Lu li,Li Shuqing,Li Zhonghao.Modulation instability and soliton on cw background in inhomogeneous optical fibermedia[J].Am Opt Commun,2004,234:169-172.

[7]Yuri SKivshar,Barry Luther-Davies.Dark optical soliton:Physics and Applications[J].Physics reports，1998,298:81-90.

The I nteraction of A d jacent B right and D ark S olitons

LIShu-qing,WANG Ai-guo,FENG Zhong-ying,RENG Quan-nian
(Departmentof Science，Taiyuan Technology I nstitute，Taiyuan Shanxi,030008)

Through comparison with the bright soliton and analysis the fundament equation of dark solitons,a dark soliton solution has been given.Then the interaction of adjacent dark solitons has been studied.At the last,amethod of some integration has been given.

NLSequation;dark soliton solution;interaction;integration

TN012

A

〔编辑 李海〕

1674－0874（2010）01－0039－03

2009－08－06

李淑青（1978－）女，山西长治人，硕士，讲师，研究方向：非线性光学.