水资源优化配置中多目标模型的建立和求解
西南交通大学环境科学与工程学院 韩海燕 钟曙亮 彭俊林 汪则灵
水资源优化配置中多目标模型的建立和求解
西南交通大学环境科学与工程学院 韩海燕 钟曙亮 彭俊林 汪则灵
本章从水资源优化配置的基本概念入手,讨论了水资源配置的多目标性,并针对这种多目标性研究了水资源多目标优化配置模型的建立和求解。
水资源 配置 多目标 求解
水资源优化配置是指在流域或特定的区域范围内,运用系统工程理论和优化方法,以水资源的可持续利用和经济社会的可持续发展为目标,遵循公平、高效、统筹兼顾和可持续利用的原则,采取除害与兴利、水量与水质、开源与节流、工程与非工程措施相结合的方法,通过合理抑制需求、有效增加供水、积极保护生态环境等手段和措施,对多种可利用水资源在区域间和各用水部门间进行最优化调配和分配,力求水资源与其他资源合理配置,实现有限水资源的经济、社会和生态环境综合效益最大[1]。
水资源的优化配置研究可为水量和水质在时间和空间上的合理调配和使用以及保障水资源的可持续利用提供科学依据和对策、措施。因此,水资源的优化配置研究在解决我国的水资源问题,实现水资源的可持续利用等方面均占有重要地位,对促进经济社会的可持续发展具有重要理论和实际意义。
1.水资源优化配置中多目标问题分析
区域水资源系统往往是一个用水部门众多的大系统,在现代水资源优化配置思路中,己经改变了过去以经济效益为中心的基本观念,不仅仅是要获得尽可能大的经济效益,还必须将生态环境保护放到重要位置,同时要兼顾引水保障和粮食安全的问题。配置中所考虑的不同问题可以作为不同的目标,各个目标之间相互矛盾而又不可公度,这就使得区域水资源优化配置转变成一个多目标优化的问题,在协调各个配置目标时要以公平与高效为基本分配原则,目标是寻求水量在各个用水部门之间的最优分配,实现水资源利用的可持续发展。
2 模型的建立及求解
2.1 水资源多目标优化配置模型的建立
2.1.1 决策变量
根据区域的地形地貌、水利条件、行政区划,一般可将区域划分为若干分区。根据各水源在区内的配水特性,可将水源划分成两类:共用水源和独立水源。所谓共用水源是指能同时向两个或两个以上的分区供水的水源。独立水源是指只能给水源所在的分区供水的水源。
本研究假设区域划分为K个分区,i =1,2,…,K,本文将k分区内所有独立水源计为1个水源、分别有J(K)个用水部门j=1,2, …,J(K)(本文各区均定为4个,分别为工业、生活、农业、生态)。本研究把各分区独立水源概化成一个水库水源,供给本分区用户,同时,假设整个区域内有M个公用水源,c=1,2,…,M,其水量和其它独立水源的水量一样,需要各用户间进行分配。因此,对于i分区而言是1+M个水源和4个用户的水资源优化分配问题。设为i分区独立水源对本区第j个用水部门的供水量;为第c个公共水源对第i分区第j个用水部门的供水量,故区域水资源优化配置决策变量个数为:4K+4MK。
2.1.2 目标函数
本文选用多目标优化规划,各用水部门之间的最优分配模型主要是考虑用水部门综合效益最大化。将多目标分为工业用水效益、生活用水效益、生态环境用水效益和农业用水效益这四个目标。其目标函数形式为:
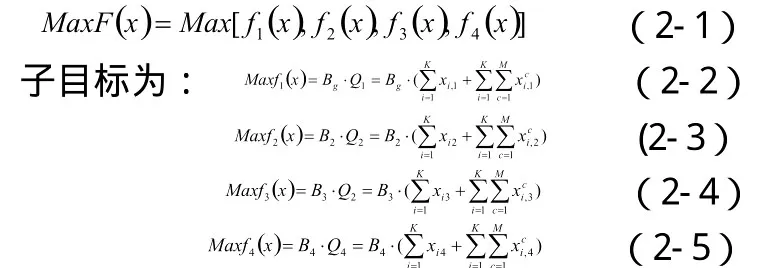
式中f1(x)——工业用水效益目标;f2(x)——生活用水效益目标;
f3(x)——农业用水效益目标;f4(x)——生态用水效益目标;
x——决策变量,非负;K——分区个数;M——公共水源个数;
Bg,B2,B3,B4——工业、生活、农业和生态用水的综合效益系数。
2.1.3 约束条件
本研究设置约束条件如下:
(1)供水约束——水源可供水量约束
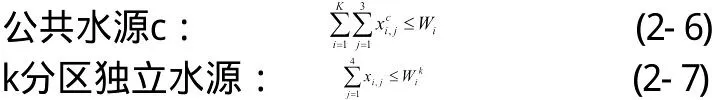
式中Wc——公共水源c可供水量;
——k分区独立水源i的可供水量;
——i分区独立水源对本区第j个用水部门的供水量;
——第c个公共水源对第i区第j个用水部门的供水量。
(2)需水约束——用户需水约束
对于生活、工业、农业和生态各用水部门应该设定最低供水保证,但分配水量也不应超过各部门的最大需水量。
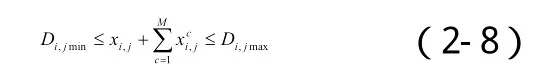
式中Di,jmin——k分区j用户的最小需水量;
Di,jmax——k分区j用户的最大需水量。
3.变量非负约束


2.2 模型的求解
水资源多目标优化配置模型具有多目标、多约束、多关联、非线性的特点,是一个规模庞大、结构复杂、影响因素众多的大系统多目标模型。许多学者分析采用了不同的计算方法研究求解水资源优化配置的模型[2~4]。
多目标优化问题有多种解法,利用目标达到法来求解多目标规划问题常常是指,已知目标函数系列为,对应有其目标值系列允许目标函数有正负偏差,偏差的大小由加权系数向量控制,于是目标达到问题就可以表达为标准的最优问题:
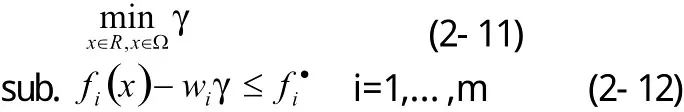
目标达到法的最大好处是可以将多目标最优化问题转化为非线性规划问题,但是,在序列二次规划(SQP)过程中,一维搜索的目标函数选择不是一件容易的事情,因为很多情况下,很难决定是使目标函数变大好还是变小好。这就导致目标达到法改进的提出,可以通过将目标达到问题变为最大最小化问题来获得更合适的目标函数。

3.结论
多目标优化配置模型能实现区域社会、经济、环境综合效果最大,并得到相应的水资源分配方案。可以得到整个区域、各子区及用户的缺水程度。文中采用目标达到法的改进法对模型进行求解,在Matlab优化工具箱中,函数fgoalattain实现了目标达到法求解的改进,使得多目标优化算法更具有鲁棒性。
[1]许新宜等.浅谈水资源承载能力与合理配置[J].中国水利.2002,10:42-44.
[2]马斌,解建仓,汪妮,等.多水源引水灌区水资源调配模型及应用[J].水利学报.2001,(9): 59-63.
[3]吴泽宁.基于生态经济的区域水质水量统一优化配置研究「D].河海大学博士研究生学位论文,2004,2.
[4]苏金明,张莲花,刘波.Matlab工具箱应用[M].北京:电子工业出版社,2004.1.

