HVDC输电线路合成场强数值计算方法研究

张 栋,周 坤,黄壁荣

(1.广东佛山电力设计院有限公司,广东佛山 528200;2.湖南省电力勘测设计院,湖南长沙 410007;3.江苏省无锡供电公司,江苏无锡 214061)

高压直流 (HVDC)输电线路产生的电场与交流输电线路产生的电场具有完全不同的特性。就交流输电线路而言,线路导线电晕时,由于电压的交替变化,所产生的离子绝大部分被限制在导线附近,离子基本上不离开导线运动。而直流输电线路的电场则比较复杂,导线电晕时,离子在电场力的作用下,向反极性的导线和地面运动。这样在两极导线和极导线与地之间都存在离子,亦即空间电荷,它们同时也产生电场,从而改变地面的场强,形成合成场强。我国 DL/T 436-2005《高压直流架空送电线路技术导则》〔1〕规定直流输电线路下地面最大合成场强不应超过 30 kV/m、最大离子流不应超过 100nA/m2。

多年来为了能够为直流线路设计提供既简单方便、又能较为准确地预测地面电场的有效途径,许多科研工作者提出了不少能够应用于实际情况的计算方法,总体来说可以分为 3类:(1)Deustch假设法;(2)半经验公式法;(3)有限元法〔2〕。其中方法 (1)是在 Deustch假设情况下的一维计算,应用条件比较理想,没有考虑风速的影响;方法(2)需要大量的试验以积累数据,应用起来困难。文中采用上流有限元法〔3〕计算 HVDC输电线路下的合成电场和离子流密度,认为导线起晕后表面场强保持不变 (Kaptzov假设),并用开发的计算软件分析影响合成电场的因素,同轴圆柱结构的解析解和实验线路测量数据的比较结果验证了该计算方法的有效性。

1 计算方法

1.1 基本假设〔4-5〕

(1)忽略导线周围电晕层的厚度;

(2)电晕已达稳定,不考虑暂态过程;

(3)起晕后导线表面场强保持在起晕场强值;

(4)不考虑空间电荷的扩散;

(5)正负离子迁移率及复合系数恒定。

1.2 基本方程

采用相关假设后,电势 Φ、合成场强 →Es及正负极电流密度 →j+, →j-可以由以下方程描述〔6〕:

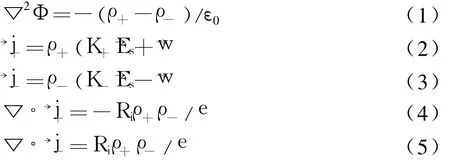
式中 ρ+和 ρ-为正 /负空间电荷密度;K+和 K-为正/负离子迁移率;Ri为离子复合率;→w为风速向量;e为电子电量。

首先需要定义边界条件,一般而言,在导线表面有:

式中 U为导线电压;E0+和 E0-为正/负极起晕场强。可以用 Peek公式〔7〕计算。地面的边界条件为Φ=0和人工边界条件 Φ=U0(为空间电荷不存在时的标称电势)。

1.3 用上流元计算空间电荷密度

空间各点电荷密度是采用同轴圆柱离子流场的空间电荷密度解析解来设置的,而这并不是准确解。根据泊松方程的有限元解法求出各点电位的数值解及合成场强E→s后,迭代过程可能很不稳定,而导致不收敛。为此,引进了上流元有限元法〔3〕。对于图 1所示的的一个剖分单元,ijm逆时针排列,别为向量ji逆 时针选择 90°而得。若点的空间电荷迁移速度 →v与 →b和 →c的夹角皆小于 90°,则三角元 ijm定义为上流元。

图 1 节点 i的上流元

上述过程可以描述为:

这样计算出来的结果满足 0＜ρi≤max{ρj,ρm},即速度下方点的电荷密度总是不大于速度上方点的电荷密度,保证了解的收敛性,也与事实相符。

接下来是在每个上流元内对未知节点电荷密度的求解。此时将电荷密度的一阶导数近似地用三角元上电荷密度的插值函数得到〔6〕:

式中 ρi,j,m为各点电荷密度;Ni,j,m为该三角元的面积坐标。这样,可以从导线周围开始,逐一求解各节点的电荷密度,直至求出所有节点的电荷密度。

1.4 计算过程

由于上述方程中电势和电荷密度相互耦合,因此采用迭代方法求解。首先将无限场转化为有限场进行单元剖分,假设空间各点电荷密度初值〔8〕,用有限元计算出空间各点的电势和场强,然后由UFEM〔3〕计算出空间各点的电荷密度,如果满足收敛条件:

则计算完成,否则修正导线表面的空间电荷密度,修正公式如下〔9〕:

然后再计算空间各点的电势和场强,直至满足收敛条件。式 (11)中 Eca为计算出来的导线表面最大合成场强;ρn-1,ρn为第 n-1,n次迭代后的电荷密度值。

计算出合成场强和空间电荷密度后,可由电流连续性方程〔10〕计算离子流密度

j=KEsρ

2 同轴圆筒电极离子流场比较

同轴圆柱是具有离子场分布解析解的计算模型〔9〕,可以从最理想的条件下判断一种算法是否正确。算例数据如图 2所示,图 3给出了电位、场强和电荷密度与解析解的对比。

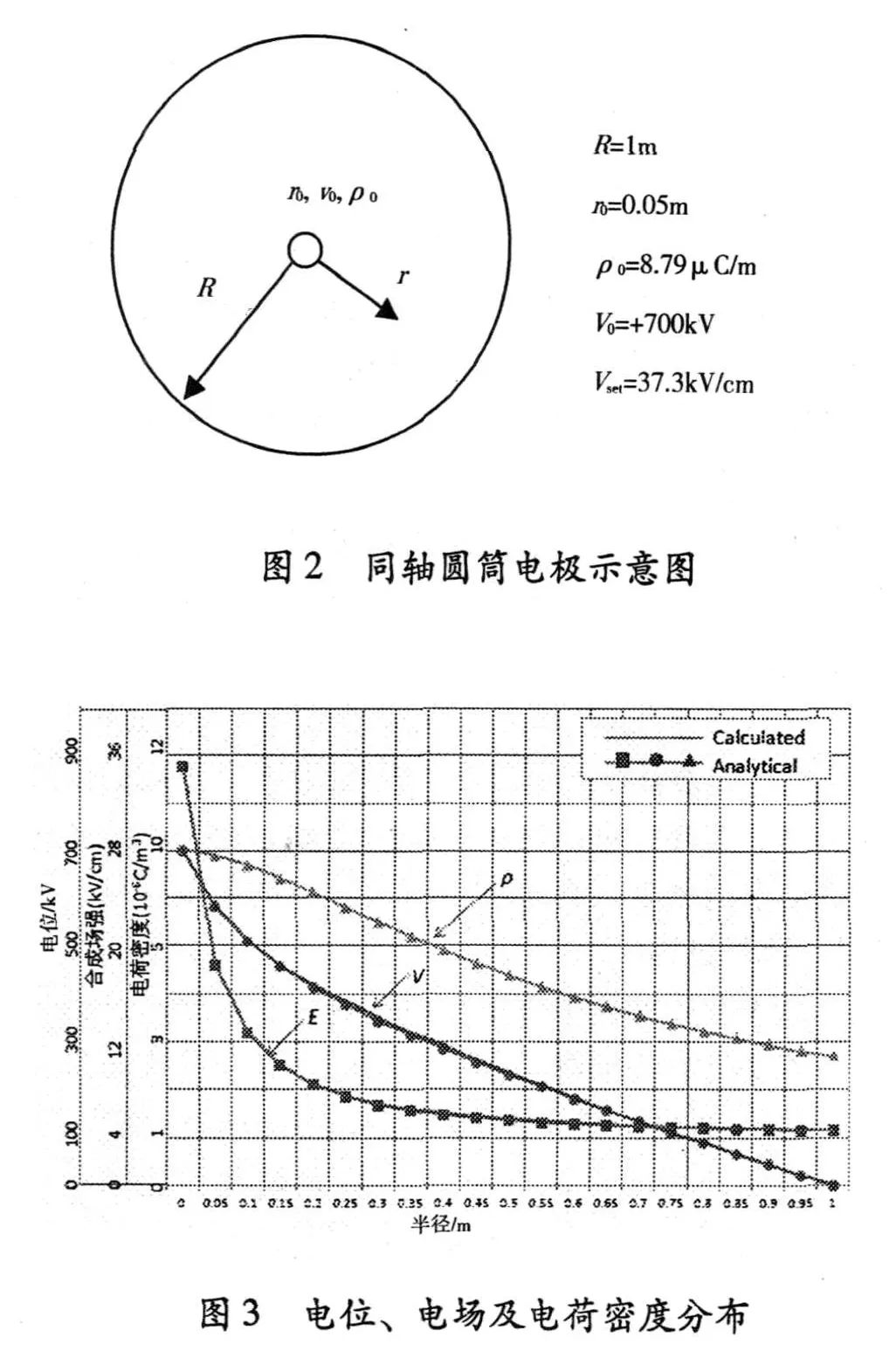
图 3表明解析数据和计算数据比较相符,特别是靠近电极处,电位和场强变化较快,这与物理事实比较相符。

3 实际双极线路的计算

以 1条双极 ±500 kV直流线路为例进行分析。采用四分裂导线,子导线直径 27.63 mm,分裂距450mm,极间距 14.6 m,正极对地 16.8 m,负极对地 17.0 m。计算与测试结果如表 1所示。

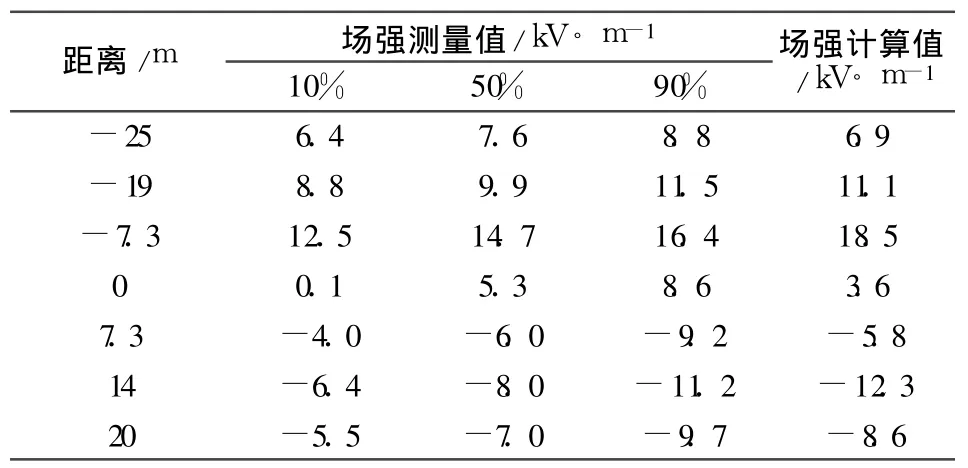
表 1 地面合成场强测量值与计算值比较

计算时考虑电晕发展最严重情况,正负气晕场强取值相同,从图 4可以看出,理论计算和实测值基本是一致的。

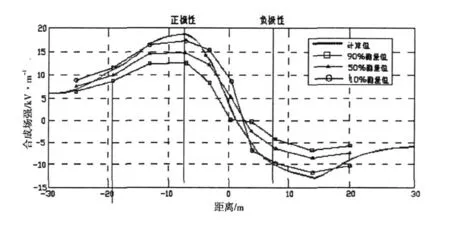
图 4 文献 〔11〕测量数据与计算数据的比较

综合以上分析,基于上流有限元的计算方法和同轴圆柱模型及实际线路的测试结果符合较好,证明了采用上流有限元的计算方法基本是正确的。

4 结 论

采用有限元方法,将高压直流离子流场的计算转化为在给定边界条件下对泊松方程和电流连续方程的迭代求解,得出以下结论:

(1)有限元法不需 Deutsch假设;

(2)采用的上流有限元法可以考虑风速对合成电场和离子流密度的影响。

(3)不同的导线高度、极间距、表面状况等对双极输电线路下地面合成场强和离子流密度的分布规律均具有一定的影响,在设计实际线路时应合理考虑这些因素。

〔1〕DL/T 436-2005,高压直流架空送电线路技术导则 〔S〕.北京:中国电力出版社.

〔2〕赵畹君.高压直流输电工程技术 〔M〕.北京:中国电力出版社,2004.

〔3〕 Tadasu T.Calculation of ion flow fields of HVDC transmission lines by the finite element method〔J〕.IEEE Trans on Power Apparatus and Systems,1981,100(12):4802-4811.

〔4〕 Maruvada P Sarma,Wasyl Janlschewskyj.Analysis of corona losses on DC transmission lines partⅡ -Bipolar lines〔J〕.IEEE Trans on P＆AS,1969,88(10):1476-1492.

〔5〕 Maruvada P Sarma,Wasyl Janischewskyj.Analysis of corona losses on Dc transmission lines partⅠ -Unipolar lines〔J〕.IEEE Trans on P＆AS,1969,88(5):718-731.

〔6〕 Lu Tiebing,Feng Han,Zhao Zhibin,etal.Analysis of the electric field and ion current density under ultra high-voltage direct-current transmission lines based on finite element method〔J〕.IEEE rans on Magnetics,2007,43(4):1221-1224.

〔7〕 M.P.Sarma,Corona Performance of High-Voltage Transmission Lines.Hertfordshire,U.K.:Research Studies,2000.

〔8〕 Ming Yu,E.Kuffel.A New Algorithm for Evaluating the Fields Associated with HVDC Power transmission Lines in the Presence of Corona and Strong Wind〔J〕.IEEE TRANSACTIONS ON MAGNETICS,1993,29(2):1985-1988.

〔9〕 W.Janischewskyj,W,Gela G.Finite Element Solution for Electric Fields of Coronaing DC Transmission Line〔J〕.IEEE Transactions on Power Apparatusand Systems,1978,98(3):1000-1012.

〔10〕 Maruvada P S.Corona performance of high voltage transmission lines〔R〕.Research Studies Press LTD,2000.

〔11〕薛辰东,等,天广直流地面合成场强的测试 〔R〕.中国电力科学研究院,1989.

〔12〕倪光正,等,工程电磁场数值计算 〔M〕.北京:机械工业出版社,2004.