全球商务环境下的集成采购计划模型研究综述
钟金宏, 黄 玲, 杨 柳
(1.合肥工业大学 管理学院,安徽 合肥 230009;2.解放军电子工程学院 302教研室,安徽 合肥 230037)
0 引 言
随着经济全球化程度的加深,多数全球企业尝试同供应链伙伴的协作,通过分散网络化制造或/和采购(外包)来增加自己的柔性能力,使它们能快速响应客户需求和避免失去销售。
近年来,部件和服务方面的外包有了稳定的增加,企业根据部件和服务的内部生产经济性及其战略性(是否核心产品或服务),将业务中心放在其优势最明显而且附加值高的业务上,而将其它辅助业务外包。在高技术产业中,服务和部件的外包已超过成品成本的80%[1]。最近的制造外包活动数据(契约制造)也证实了这一趋势:契约制造产业的价值在2001年估计是120亿美元,成为制造产业中增长最快的部分,在1996-2000年间年增长率超过80%,到2010年制造活动外包比例将有望达到50%[2]。互联网和相关信息技术的进步,对采购的影响日益增加,出现了基于互联网的采购(电子采购),这降低了供应商选择和订单派发的事务成本,使多供应商更具吸引力[3]。
目前,已出现了几类处理非关键产品的电子采购市场,如工业化学品、金属和印制电路板等,拍卖是这些商场运营的最流行机制之一。因此,随着外包的兴起,采购决策备受关注,企业采购的有效性对提升企业竞争力有重要意义。
外包非优势业务使企业间的分工越来越细,企业间的协作更广。从企业组织形态来看,出现了相互依赖的组织,如企业联盟和敏捷企业;供应链的作用日益明显,产品市场的竞争已不是简单的企业间竞争,而是企业供应链间的竞争。在这方面,学术界和业界已得出:公司要保持竞争力,就必须和其供应链伙伴一起协作,改进供应链的总体性能,为顾客提供更好的服务和产品。因此,在采购活动中,实现供应链总体成本最小或利益最大是必须考虑的问题。
采购职能是供应链上流的主要活动,影响企业的方方面面,已被许多管理者视为企业尝试获得优势竞争地位的关键战略工具[4],而且,随着更多企业采用整体质量管理和JIT概念,供应商和供应链管理的地位显得更加重要[5]。据文献[6],制造商的供应链成本占其总成本的80%,零售商则为70%~80%。
尽管生产和采购计划可以创造很大的经济效益,但在诸如SAP集成企业资源规划(ERP)软件包中,在采购管理方面的功能非常有限,大多仅仅实现了采购信息管理,缺少优化方面的功能。某些企业即便配备有信息系统软件来预测需求,也仍然凭经验制定采购计划来减少成本。
采购计划问题与生产计划问题可归为一类,仅产品的获取方式不同,本文不纯指传统的采购计划。面向供应链的集成采购计划是实现采购、运输、生产、外包和供应商选择等方面的集成优化;优化不再局限于企业内部,而是供应链的上下游的集成优化和协调;优化也不再是传统的各方面独自优化,而是整体优化。由于经济的全球化,企业在全球范围内有效整合有关资源、组织生产和销售产品,故这种优化也不再局限于某一地区,而是面向全球供应链。
1 采购计划问题的基本模型
企业的采购计划主要解决对所需原料和元件的采购时间、采购量及采购对象等3个问题。总的目标是要按时、按质、按量满足需要,从而使得总成本最小化。采购计划问题可用经济批量模型(ELS)描述,文献中有多种ELS公式及其变种。本文以受限批量问题(capacicated lot sizing problem,简称CLSP)为例,给出该类问题的数学描述 ,即
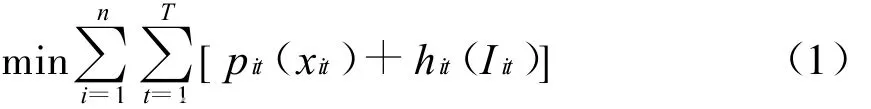

其中,n为产品数;T为周期数;在周期t,dit为产品i的外部需求;xit为产品i的生产量;Rt为资源的可获得量;Iit为 t周期末产品i的库存量;pit(◦)和hit(◦)分别为t周期产品i的生产和库存成本函数;Ri(◦)为产品 i的资源消耗函数。目标函数(1)为最小化规划期内的总体生产和库存成本;约束(2)为物料平衡公式;约束(3)为资源限制;约束(4)为非负性约束。
在上述模型中,产品数n=1时,为单产品批量问题;去掉能力约束(3),该模型为非受限批量问题;当允许延期交货时,需去掉约束Iit≥0。生产和库存成本结构有多种形式,常见的形式是凹函数,通常生产成本中包含调整成本。
多级受限批量问题的数学模型与CLSP类似,但约束(2)和(3)分别为:

其中,aij为生产单位产品j需要产品i的数量;τi为产品i的时滞;S(i)为产品i的直接后继集合;Rjt为t周期资源j的可获得量;Rij(◦)为产品i的资源j消耗函数。
2 采购计划的研究进展
经济批量问题是生产规划中最重要和最困难的问题之一,最早研究可追溯到针对静态需求的经济订货数量(EOQ)[7]。目前,已有很多研究围绕经济批量问题[8]展开。文献[9,10]总结了影响批量问题分类、建模和复杂性的主要因素,如规划期、产品数、级数、能力或资源约束、需求、是否为易腐产品、调整结构和是否允许短缺等。
2.1 单产品经济批量问题
单产品经济批量问题受到广泛关注,这是由于在许多实际批量库存问题的建模和求解中,它经常被看作是这些问题的子问题(如基于 Lagrangian松弛的启发式方法),并且通常能在多项式时间内获取其精确解。此外,其本身也可看成是一类产品或相同(相似)产品的批量问题。单级单产品研究可归类为:非受限批量问题、有界库存问题、受限批量问题以及扩展研究。
非受限单产品批量问题是多项式可解的,最适合的求解方法是动态规划。对一般的凹成本函数问题,算法的复杂性为O(T2)[8,11],文献[11]考虑了延期交货情况;对线性时变成本结构,算法的复杂性可减至O(Tlg T),如成本函数是静态的或非投机性的,则复杂性可进一步降为O(T)[12]。
库存能力受限的问题称为有界库存模型。对一般的凹成本结构,动态规划算法的复杂性是O(T3)[13];当生产成本为带固定费用的线性成本时,该问题是O(T2)可解的,如进一步假定生产成本非增或非投机性时,复杂性可降为O(T)[14];当成本结构中无固定费用时,复杂性为O(Tlg T)[15]。
生产能力受限的单产品批量问题是NP难的,仅在一些特殊情况下是多项式可解的[16,17]。文献[17]引入了符号α/β/γ/δ来描述问题,分别表示调整成本/库存成本/生产成本/能力,这些参数可取以下值 :Z 、C 、NI、ND 和 G,这些值分别表示零、常数、非增、非减和非预定模式。基于该符号系统,该类模型中的多项式可解情况总结为:文献[18]对G/G/G/C问题提出了O(T4)算法;文献[19]扩展他们的结果到非凹非凸成本函数;文献[20]针对线性库存成本将复杂性改进到O(T3)。文献[17]对NI/G/NI/ND、NI/G/NI/C、C/Z/C/G和ND/Z/ND/NI等情况分别给出了O(T4)、O(T3)、O(TlgT)和 O(T)算 法。 对NI/G/NI/ND问题,文献[21]设计了O(T2)的动态规划算法;文献[22]基于动态规划的几何特征给出了更有效的算法。
对不能多项式求解的受限批量问题,文献[16]开发了伪多项式动态规划算法;文献[23]采用元启发方法求解受限批量问题;文献[24]考虑了近似方法,得到了相对误差可评价的原问题的近似解。在扩展经济批量模型方面,文献考虑的因素主要有:需求时间窗、再制造、滚动规划期、安全库存、库存增益、非均匀资源消耗、可再生自然资源、失去销售/外包、保暖/冷却过程和经济批量博弈等。
2.2 单级多产品经济批量问题
单级多产品经济批量问题是确定规划期上每周期的生产/采购量,以最小总成本满足已知的多产品需求。当不考虑多产品间的联合启动成本时,N种产品的非受限批量问题可很容易地划分成N个非受限的单产品批量问题,可采用前述求解算法精确求解[25],当产品间存在联合启动成本时,该问题是NP难的[26],因此,大多数研究集中在探索问题的特殊性质,开发最优的启发式算法。当每个产品都具有WW 类型时,问题存在最优解[27]。目前求解该类问题的所有方法均使用了该性质,但这些方法都只能求解小规模实际问题。为此,许多研究者转向该问题的松弛版本,通过松弛联合启动成本,将问题变成不相关的多产品问题,得到问题的更紧下界[28]。
单级多产品受限批量(CLSP)问题属于大桶问题,一个周期可生产几种产品。它是强NP难的,甚至对具有调整时间的CLSP寻找可行解也是NP难[29]的,因此不可能开发有效的最优化算法。CLSP的求解算法可分为:精确算法、一般(或特定)启发式方法、元启发式方法和基于数学规划的启发式方法4类。
常用精确算法有分支定界、切平面生成技术和变量重新定义。一般启发式方法有逐周期、逐产品和改进启发3类,它包括3步:求批量阶段、可行性修正和解改进;解的可行性修正有前向和后向2种机制;改进启发方法的初始解通常是由非受限批量技术获得。在求解该类问题上,研究者采用了元启发式方法。基于数学规划的启发包括:松弛启发、分支定界启发、集划分与列生成启发和其它启发方法。
单级受限多产品批量问题有以下变种:离散批量与调度问题(DLSP)、连续调整批量问题(CSLP)、比例批量和调度问题(PLSP)、一般批量和调度问题(GLSP)及经济批规划问题(ELSP)。
2.3 多级多产品经济批量问题
多级多产品经济批量问题(multi-level lot sizing problem,简称MLLP)是指产品的生产/采购要经过多个阶段(工序),需确定多个阶段的生产安排,以最小总体成本满足已知需求。该问题存在依赖性需求(级间来自产品材料清单BOM的需求)和独立需求(来自外部的产品需求)。产品结构有串型、组装型、树型和一般型。
非受限MLLP仅当问题规模非常小时,可在合理的CPU时间内优化求解,大规模问题只能考虑启发式算法。考虑一般产品结构的非受限MLLP是NP难问题[30]。目前大多数研究都是针对串型和组装型产品结构,这些研究多基于嵌套性质[31],如果仅最终产品需求独立、生产/采购成本固定,且某级在直接后继开始运作后才运作,那么该非受限MLLP有最优解。当组件需求独立时,串型系统可通过一O(NT4)的动态规划算法来求解多项式[32],N为产品数。在一些假定下,组装结构的系统多项式可解[30]。对不能多项式时间内求解的单最终产品的非受限MLLP问题,常用的精确求解算法有动态规划、松弛或重新公式化方法。动态规划方法的计算复杂性是随问题尺寸指数增长的,因此不适合求解大规模问题。基于松弛方法主要是使用Lagrangian松弛技术将问题转成更容易有效求解的问题,一般松弛耦合的约束,文献[26]给出了一般产品结构问题的松弛过程。重新公式化方法是重新给出能更有效计算的问题公式,常使用梯形库存概念,转化后的模型可由特定的切平面算法求解,文献[33]给出了一般产品结构系统的转换后公式。
受限MLLP比CLSP更复杂,最近的研究多是排除问题的某些特征来简化求解过程。求解算法多为启发式或元启发式算法,并仅限于规模不大的问题。因此,对该类问题来说,开发有效的能真正应用到工业实际的启发式算法将是未来很长时间的研究方向。求解该问题的精确算法有基于拉格朗日松弛的分支定界算法和原-对偶方法。对该类问题启发式方法将更有吸引力,文献中有逐级、松弛和成本调整等3类启发方法。由于该类问题非常复杂,很多研究者考虑元启发式方法及其组合[34,35],如遗传算法、模拟退火、蚁群算法、禁忌搜索、粒子群算法、类似遗传算法的memetic算法和神经网络等。
3 面向供应链的集成采购计划
经济全球化带来了企业运作方式的深刻变化,出现了分散网络化制造和全球供应链,企业更多地跨越企业边界,在供应链层次上进行运作。面向供应链的采购计划研究备受关注。
3.1 多工厂或供应链计划问题
多工厂系统是一个复杂的采购、生产和分销网络,覆盖供应链的大部分。在该网络中,每个点都可能是一个多级生产系统,多工厂计划问题可用多级批量问题来近似描述,每级相当于一个工厂,与单工厂的多级批量问题相比,最大的差异是工厂间的运输成本不能忽略。通过集成考虑生产、运输、库存和分销可带来成本上的节省,但也使问题更加复杂,且很难优化求解。如同时考虑车辆路径问题(VRP)和受限批量问题,而这两者自身就是NP难问题。目前的研究多针对恒定需求情况,文献[36]按单产品/多产品、受限/非受限和静态/动态需求回顾了多工厂批量协调问题,并给出了一个通用的供应链计划模型。文献[37]总结了供应链计划问题的主要建模因素,文献[38]从供应链的供应商、工厂和分销阶段,回顾了全球供应链优化方面的热点问题及进展。
3.2 考虑合作伙伴的批量问题
外包已成为企业普遍采用的管理策略之一,是合作伙伴间追求双赢的一种常用方式,也是当前的热点研究问题。在单产品方面,有失去销售[39,40]和外包[14,41]模型2种提法,两者的建模角度相同,但后者更符合当前实际;这些文献对非受限、库存受限和恒定生产能力约束的批量问题,分别开发了基于动态规划的多项式算法。在多产品方面,过去的研究集中在供应商和分销商的外部集成上,没有考虑制造伙伴的内部集成;研究多集中在单级产品结构,未考虑多级BOM结构[42]。
3.3 考虑供应商选择与采购折扣的批量问题
在采购批量决策中引入经济订货数量概念,可同时实现供应商选择和采购批量确定,并可最小化采购过程中产生的总成本[43,44]。虽然多周期采购模型可以生成更好的采购方案,但迄今的大量研究都是单周期模型[44]。目前,仅文献[45]研究了多周期、多供应商的多产品库存批量问题,考虑了产品持有成本和卖主依赖的订单成本。在不同产品间存在不同的相互依赖关系,在出现数量折扣时,多产品采购模型可生成不同协同优势(如减少采购、订货和运输成本)的多产品采购方案,这对买卖双方都有利,但目前的研究多为单个产品的卖主选择问题[44]。
在采购决策中经常需要考虑折扣因素,这主要体现在采购成本上。常见折扣形式有数量、业务量和捆绑折扣3种。数量折扣环境下,一个产品的销量不影响其它产品的价格和折扣,可分为全数量(累积)和增量(非累积)折扣。文献[46]研究了价格时段机制下的有质量及能力约束的卖主选择问题,分别考虑了增量式和全数量折扣。业务量折扣是卖主基于销售量的总价值进行打折,不考虑产品的销售量和品种。该策略对买卖双方有诸多益处,但单一总价值折扣方案会造成产品价格的相互依赖,有时会妨碍顾客购买想要的产品。文献[47]考虑了单周期业务量折扣,提出了一个混合整数规划模型来优化总采购成本。捆绑折扣方案是指一个产品的价格依赖其它产品的订货量,文献[48]研究了订单式生产中带捆绑折扣的多产品卖主选择问题。文献[49]讨论了基于订单数量和总价值的延迟回扣以及基于订单总价值的边际折扣。此外,文献也有关于价格时段机制的研究,指出采购价格不仅会随采购量降低,也可能会随采购量增加。目前,仅文献[46]考虑了附加费的出现,研究了价格时段方案的影响。全数量和增量折扣在EOQ模型中有众多研究,但在经济批量模型中受到较少关注。
3.4 考虑运输折扣的批量问题
类似的整车运输折扣(TL,truckload)方案有:全数量折扣、增量折扣和欠载折扣(运输公司承担低载运费,客户只需支付整车运费)。文献[50]研究了2个有分段凹成本的ELS模型,第1个模型假定单调成本参数、无延期交货、固定生产成本参数和非静态卡车能力,开发了O(T3)算法;第2个模型考虑了静态卡车能力和一般时变成本参数,其它与第1个模型一样,提供了O(T5)算法。文献[51]考虑了具有整车运输折扣方案的多级ELS模型,开发了分支定界求解算法。文献[52]研究了多产品ELS模型,考虑了部分填充容器的空间要求。文献[53]对考虑TL折扣的ELS模型给出了O(T4)算法,在模型中无延期交货,整车运输费用为静态,获取成本为带固定费用的线性函数。文献[54]研究了ELS的2个变种,对每周期生产量只能是固定批尺寸的倍数情况,设计了一个O(T2)的动态规划算法,并用Monge矩阵将复杂性降到O(Tlg T);对带运输量折扣模型,开发了O(T3lg T)算法。
4 研究趋势及存在的问题
从应用上来说,企业的运作管理日趋精细化,人们更多地关注物料、设备、人员、场所、时间和技术等约束因素下,企业层次上的优化和供应链上的集成优化。但目前的ERP软件包尚不能有效支持这些新发展,基于约束优化理论、采用数学规划等方法实现决策优化的高级计划排程系统(APS)开始出现,各大ERP厂商纷纷开发自己的APS系统。计划模型及其求解算法是APS的核心,但目前这方面的研究还很不够。在理论研究上亦体现了这一趋势,全世界有大量人员在从事供应链管理方面的研究和实践。在采购计划模型方面,人们更多地关注供应链层次的集成优化,体现在以下几方面:
(1)生产、采购和库存管理的集成。文献[39-41]研究了带外包的批量模型,实现生产、采购和库存的总体成本最小化,而外包实际上是某种形式的采购。文献[42]考虑了面向全球供应链的多级多产品的生产、采购和库存的集成优化。
(2)采购(生产)、运输与库存管理的集成。文献[50-54]研究了带整车运输折扣的离散动态经济采购量问题。
(3)多周期库存控制模型与供应商选择模型的集成。文献[46]研究了多周期多产品离散库存批量模型与供应商选择模型的结合。
目前研究中存在的问题如下:
(1)考虑多产品间依赖和多周期库存控制的卖主选择模型与采购计划的集成优化研究较少。
(2)在采购、生产和库存控制方面的集成优化有少量研究;在采购、运输和库存管理方面的集成研究亦较少。这2方面的研究都有待加强。
(3)数量折扣与经济定货量的结合有大量文献,与离散动态批量模型的结合研究较少。
(4)在更宽方面的集成优化有待研究。如采购、运输、生产和库存控制的集成优化,以及数量折扣与这些模型的结合。
[1]Burton T T.JIT repetitive sourcing strategies:tying the knot with your supplier[J].Production and Invento ry Management,1988,29(4):38-41.
[2]Hayes R,Pisano G,Upton D,et al.Operations,strategy,and technology[M].New York :Wiley,2005 :130-145.
[3]Minner S.M ultiple-supplier inventory models in supply chain management:a review[J].Int J Production Economics,2003,81/82(1):265-279.
[4]Verma R,Pullman M E.An analysis of the supplier selection process[J].Omega,1998,26(6):739-750.
[5]Gustin C M,Daugherty P J,Ellinger A E.Supplier selection decisions in systems/software purchases[J].International Journal of Purchasing and Materials Management,1997,33(4):41-46.
[6]Sengupta S,Turnbull J.Seamless optimization of the entire supply chain[J].IIE Solutions,1996,28(10):28-32.
[7]Harris F W.Operations and cost:in factory management series[M].Chicago :A W Shaw Co,1915 :48-52.
[8]Wag ner H M,Whitin T M.Dynamic version of the economiclot-sizemodel[J].ManagementScience,1958,5(1):89-96.
[9]Karimi B,Fatemi Ghomi S M T,Wilson J M.T he capacitated lot sizing problem:a review of models and algorithms[J].Omega,2003,31(5):365-378.
[10]Bahl H C,Ritzman L P,Gupta J N D.Determining lot sizes and resource requirements:a review[J].Operations Research,1987,35(3):329-345.
[11]Zangwill W I.A deterministic multi-period production scheduling model with backlogging[J].Management Science,1966,13(1):105-119.
[12]Federgruen A,T zur M.A simple forward algorithm to solve general dynamic lot sizing models with n periods in O(nlog n)or O(n)time[J].Management Science,1991,37(8):909-925.
[13]Love S F.Bounded production and inventory models with piecewise concave costs[J].ManagementScience,1973,20(3):313-318.
[14]Chu F,Chu C.Polynomial algorithms for single item lot sizing models with bounded inventory and backlogging or outsourcing[J].IEEE T-ASE,2007,4(2):233-251.
[15]Gutié rrez J,Sedeo-Noda A,Colebrook M,et al.An efficient approach for solving the lot-sizing problem with timevarying storage capacities[J].Eur J Oper Res,2008,189(3):682-693.
[16]Florian M,Lenstra J,Rinnooy Kan A.Deterministic production planning:algorithms and complexity[J].M anagement Science,1980,26(7):669-679.
[17]Bitran G,Yanasse H.Computational complexity of the capacitated lot size problem[J].Management Science,1982,28(10):1174-1186.
[18]Florian M,Klein M.Deterministic production planning with concave costs and capacity constraints[J].M anagement Science,1971,18(1):12-20.
[19]Janannathan R,Rao M.A class of deterministic production planning problems [J].Management Science,1973,19(11):1295-1300.
[20]Van Hoesel C,Wagelmans A.An O(T3)algorithm for the economic lot-sizing problem with constant capacities[J].Management Science,1996,42(1):142-150.
[21]Chung C,Lin C.An O(T2)algorithm for the NI/G/NI/ND capacitated lot size problem[J].Management Science,1988,34(2):420-426.
[22]Van den Heuvel W,Wagelmans A P M.An efficient dynamic prog ramming algorithm for a special case of the capacitated lot-sizing problem[J].Comput Oper Res,2006,33(12):3583-3599.
[23]Hindi K S.Solving the single-item capacitated dynamic lotsizing problem with startup and reservation costs by tabu search[J].Computers and Industrial Engineering,1995,28(4):701-707.
[24]Van Hoesel C P,Wagelmans A P.Fully polynomial approximation schemes for sing le-item capacitated economic lot-sizing problems[J].Mathematics of Operations Research,2001,26(2):339-357.
[25]Kirca O,Kokten M.A new heuristic approach for the multi-item dynamic lot sizing problem[J].Eur J Oper Res,1994,75(2):332-341.
[26]Afentakis,P,Gavish B.Optimal lot-sizing algorithms for complex productstructures[J].Operations Research,1986,34(2):237-249.
[27]Zangwill W I.A deterministic multiproduct,multi-facility production and inventory model[J].Operations Research,1966,14(3):486-507.
[28]Robinson E P,Gao L.A dual ascent procedure for multiproduct dy namic demand coordinated replenishment with backlogging[J].Management Science,1996,42(11):1556-1564.
[29]Chen W H,T hizy J M.Analy sis of relaxations for the multi-item capacitated lot-sizing problem[J].Annals of Operations Research,1990,26(1):29-72.
[30]Arkin E,Joneja D,Roundy R.Computational complexity of uncapacitated multi-echelon production planning problems[J].Oper Res Lett,1989:8(2):61-66.
[31]Veinott A F.Minimum concave cost solution of Leontieff substitution models of multi-facility inventory systems[J].Operations Research,1969,17(2):267-291.
[32]Love S F.A facilities in series inventory model with nested schedules[J].Management Science, 1972, 18(5):327-338.
[33]Steinberg E,Napier H A.Optimal multi-level lot sizing for requirements planning systems[J].Management Science,1980,26(12):1258-1271.
[34]Ay tug H,Khouja M,Vergara F.Use of genetic algorithms to solve production and operations management problems:a review[J].International Journal of Production Research,2003,41(17):3955-4009.
[35]Jans R,Degraeve Z.Meta-heuristics for dynamic lot sizing:a review and comparison of solution approaches[J].Eur J Oper Res,2007,177(3):1855-1875.
[36]Rizk N,Martel A.Supply chain flow planning methods:a review of the lot-sizing literature[EB/OL].[2008-07-29].http://www.cirrelt.ca/DocumentsT ravail/2001/DT-2001-AM-1.pdf.
[37]Comelli M,Gourgand M,Lemoine D.A review of tactical planning models[C]//International Conference on Service Systems and Service Management,T royes,France,October 25-27,2006:290-295.
[38]Erengüc S,Simpson N C,Vakharia A J.Integrated production/distribution planning in supply chains:an invited review[J].Eur J Oper Res,1999,115(2):219-236.
[39]A ksen D,Altinkemer K,Chand S.The single-item lot-sizing problem with immediate lost sales[J].Eur J Oper Res,2003,147(3):558-566.
[40]Sandbothe R A.T hompson G L.Decision horizons for the capacitated lot size model with inventory bounds and stockouts[J].Comput Oper Res,1993,20(5):455-465.
[41]Atamtü rk A,Hochbaum D S.Capacity acquisition,subcontracting,and lot sizing[J].M anagement Science,2001,47(8):1081-1100.
[42]Jung H S,Song I,Jeong B J.Genetic algorithm-based integrated production planning considering manufacturing partners[J].IntJ Adv Manuf Technol,2007,32:547-556.
[43]Weber C A,Current J R,Benton W C.Vendo r selection criteria and methods[J].EurJ OperRes,1991,50(1):2-18.
[44]Aissaoui N,Haouari M,Hassini E.Supplier selection and o rder lot sizing modeling:a review[J].Comput Oper Res,2007,34(12):3516-3540.
[45]Basnet C,Leung J M Y.Inventory lot-sizing with supplier selection[J].Comput Oper Res,2005,32(1):1-14.
[46]Chaudhry S S,Frost F G,Zydiak J L.Vendor selection with price breaks[J].EurJ Oper Res,1993,70(1):52-66.
[47]Sadrian A A,Yoon Y S.A procurement decision support system in business volume discount environments[J].Operations Research,1994,42(1):14-23.
[48]M urthy N N,Soni S,Ghosh S.A framework for facilitating sourcing and allocation decisions for make-to-order items[J].Decision Sciences,2004,35(4):609-637.
[49]Turner I.An independent system for the evaluation of contract tenders[J].Journal of The Operational Research Society,1988,39(6):551-561.
[50]Lippman S A.Optimal inventory policy with multiple setup costs[J].Management Science,1969,16(1):118-138.
[51]Diaby M,Martel A.Dy namic lot sizing for multi-echelon distribution systems with purchasing and transportation price discounts[J].Operations Research,1993,41(1):48-59.
[52]Ben-Khedher N,Yano C A.The multi-item joint replenishment problem with transportation and container effects[J].T ransportation Science,1994,28(1):37-54.
[53]Lee C Y.A solution to the multiple set-up problem with dynamic demand[J].IIE Trans,1989,21(3):266-270.
[54]Li C L,Hsu V N,Xiao W Q.Dynamic lot sizing with batch o rdering and truckload discounts[J].Operations Research,2004,52(4):639-654.

