证据与假说——试谈塞斯博瑞解决绿蓝问题的基本想法

杨海波

（武汉大学 哲学学院，湖北 武汉 430072）

证据与假说
——试谈塞斯博瑞解决绿蓝问题的基本想法

杨海波

（武汉大学 哲学学院，湖北 武汉 430072）

归纳问题与绿蓝问题都是涉及证据对假说的支持程度的问题，绿蓝问题可以看作是归纳问题的一个升级版本，它使得归纳问题以更为明显地方式凸显出来。人们为了对付绿蓝问题，提出了各种解决办法。赛斯博瑞（R.M.Sainsbury）在《悖论》一书中曾给出一个解决方案，文章试图反驳赛斯博瑞解决绿蓝问题的基本想法，论证他的想法过于强大，以至于排除掉了一些我们想要得到的假说。

证据；假说；绿蓝问题；归纳问题

一 什么是绿蓝问题

绿蓝问题是一个涉及证据对经验性假说支持的问题。所谓经验性假说，就是那些不能只依靠概念分析与逻辑推理就能肯定其为真假的语句或命题。不论在日常生活中还是在科学实践活动中，我们总会提出并相信各种各样的经验性假说。比如我相信我的舍友不是马加爵类型的学生、我用的电梯不会出问题、乌鸦叫就一定会死人、F=ma、以太是光传播的介质以及医生给我的感冒药不是砒霜，等等。

对于各种各样的假说，我们有相关的事实或证据来支持它们，尽管已有的证据不足以保证假说一定为真。但是，我们似乎倾向于认为，如果积极的证据越多，那么相关的假说为真的可能性也就越大。当然，我们要求证据与假说之间要有某种相关性。比如，尽管证据事实都是真的且假说似乎也是一个好的假说，但给定的证据并不支持这个假说，比如说所有数学真理似乎并不支持光速不变这个假说。在给定某些证据事实的前提下，我们似乎有理由相信相关的证据使得某个假说为真的可能性在某种程度上增加了。但有时我们说给定的证据事实不支持某一假说。在这里，我们就需要一个理论或好的说法来判别或解释什么样的证据的确是支持相关的假说的。

归纳问题与此密切相关。这个问题是说，我们怎能根据过去的事实外推到尚未发生的事实。比如根据观察，在以前，所有的A都是B，由此我们得到结论所有（将来的）A都是B。休谟告诉我们，这样的外推没有任何理性根据，并且似乎也很难找到理性的根据。尽管如此，人们似乎还是相信，过去的观察作为证据在某种意义下支持相关的归纳推论的结论。比如，过去观察到的所有的A都是B这些事实作为证据似乎支持所有（将来的）A都是B这个全称的结论（假说）。这样，如果我们有一个好的理论来判别什么样的证据能合理的支持什么样的假说，那么，我们似乎对归纳问题也就有了一个满意的解释。

例如，我们把所有A都是（或不是）B这样的经验性命题称为全称假设。相对于全称假设所有A都是（或不是）B，类似于这个A是（或不是）B这样的命题是全称假设的示例，而把类似于这个A不是（或是）B这样的命题称作是全称假设所有A都是（或不是）B的反例。很明显，全称假设逻辑蕴含它的所有示例。一个反例就能证明一个全称假设是错的。至于示例与其所例示的全称假说的另一方向的关系，我们不妨承认下述原则：

（G1）：每一个示例都支持（confirm）它所例示的全称假说。[1]P75

在某种意义上说，一个为真的示例有利于我们更为相信其所例示的全称假说是真的。为表达方便，我在下面也会说“证据支持假说”、“示例支持假说”、“事实支持假说”等，而这些都应理解为对应于相关事实的命题支持相关的假说。

尼尔森古德曼（Nelson Goodman）曾给出一个与此问题相关的悖论，人们称为绿蓝悖论或绿蓝问题，这个问题在陈述上有不同的版本，我们简要介绍其一。

假设我们到目前观察到的所有翡翠都是绿色的，那么，把相关的观察用语句表达出来，比如翡翠A是绿色的、翡翠B也是绿色的等等，那么根据G1，这些语句所表达的命题就都支持所有翡翠都是绿色的这个全称假说。

如果一些证据支持假设A，并且假设A逻辑的蕴含假设B，那么是否这些证据也支持B呢？（简称问题C）

比如所有观察到的树都矮于200米，这些证据支持所有树木都矮于200米这个假说，假设矮于关系是传递的，所有树木都矮于200米这个假说显然逻辑蕴含所有树木都矮于800米。这样看，似乎这些证据也支持所有树木都矮于800米这个假说。对这个例子，一些证据支持某个假设，同样也支持它的逻辑后承。

但是，这里也有所谓亨普尔悖论问题。不是黑色的就不是渡鸦这个命题逻辑蕴含所有渡鸦都是黑色的这个命题，根据G1，中国的红国旗不是渡鸦支持不是黑色的就不是渡鸦这个命题，那么如果问题C的答案是肯定的，中国国旗不是渡鸦也应支持所有渡鸦都是黑色的这个命题，尽管它不是关于渡鸦的命题。这似乎有些悖理。

也许有人会强辩说：毕竟，中国的红国旗不是渡鸦，如果它是渡鸦，那么就构成了所有渡鸦都是黑色的这个命题的反驳。这样的说法似乎是在说任何不构成对某全称假说反驳的命题都是对其支持的。这样，我们就要把G1说的更清楚一些，明确说明不仅示例对其所例示的全称假说才构成支持。当然，说只有示例对其所例示的全称假说才构成支持这种说法的确似乎太狭小了。因为根据这个说法，我们在树的高矮那个例子中，我们似乎也得不到我们想要的结论。毕竟，如果我们能发现翡翠的某些成分与结构使得我们看起来一定是绿色的，这样的证据的确也支持所有翡翠都是绿色的这个命题，尽管它不是这个全称假说的例示。简言之，支持一个全称假说的命题不必要求它们都是其例示，不必遵循这种“齐一性”。

当然，为了避免我在床上胡思乱想这个命题也支持所有渡鸦都是黑色的这种悖理的结论，我们似乎也要限制上述说法，即，何不构成对某全称假说反驳的命题都是对其支持的。由于接下来的论证只涉及示例对其所例示的全称假说是否提供支持，所以，我们在这里不多谈是否需要对G1进行修改。我们只要明确说明：不只示例对其所例示的全称假说才构成支持。而对问题C，人们也许有不同意见，让我们暂且假定问题C的答案是肯定的。

这样，由于所有翡翠都是绿色的这个命题逻辑蕴含所有未检查的翡翠都是绿色的，根据上述对问题C的假定与G1，我们观察到的绿翡翠支持所有未检查的翡翠都是绿色的这个假说。

我们下面定义一个新的性质绿蓝：X是绿蓝的当且仅当或者x是被检查过的并且它是绿的，或者x是尚未检查过的并且它是蓝色的。

由于翡翠A、B等等都是观察过的并且是绿色的，那么根据绿蓝的定义，翡翠A、B等等都也同时都是绿蓝色的。同样，把相关的事实用语句表达出来，即翡翠A是绿蓝色的、翡翠B也是绿蓝色的等等，根据G1，那么这些语句所表达的命题就都支持所有翡翠都是绿蓝色的这个全称假说。根据绿蓝色的定义，所有翡翠都是绿蓝色的这一命题显然逻辑的蕴含所有未检查的翡翠都是蓝色这个命题。那么根据前述对C问题的假定与G1，我们观察到的绿翡翠支持所有未检查的翡翠都是蓝色的这个假说。

这样，对同一个人（不妨叫他为甲）来说，他观察到的绿翡翠支持所有的翡翠都是绿色的这个假说，进而也支持所有未检查的翡翠都是绿色的这个假说；同样，在使用绿蓝的定义前提下，甲观察到的绿翡翠支持所有翡翠都是绿蓝色的这个假说，进而也支持所有未检查的翡翠都是蓝色的与前述假说相互矛盾的假说。并且，甲似乎认为他观察到的绿翡翠并不应该支持所有未检查的翡翠都是蓝色的这个他根本不相信的假说。在这里，甲只根据G1与绿蓝的定义无法区别这两个推理以及推理结论的好坏；他需要一个原则或办法，使得他来区分这两个推理，使得他能够得到：（1）他观察到的绿翡翠支持所有的翡翠都是绿色的这个假说，进而也支持所有未检查的翡翠都是绿色的这个假说；（2）即使使用绿蓝的定义，甲观察到的绿翡翠也不支持所有翡翠都是绿蓝色的这个假说，进而不支持所有未检查的翡翠都是蓝色的这个假说。

这就是所谓的绿蓝问题。如果可以使用如绿蓝这样稀奇古怪的定义，我们可以得出任何证据都会支持任何假说的悖理结果。比如到目前，我们观察到的人都是会死的。我们可以说这些观察支持将来所有的人都是长生不死的这个假说。我们定义一个性质P：x是P当且仅当或者x是到目前为止观察到的已死的人，并且x是会死的，或者x是现在还活着的人或将来的人并且x是长生不老的。套用上述推理，我们会得到：这些观察到的人总会死这些事实作为证据也会支持将来所有的人都是长生不死的这个假说。

对这个问题，人们提出不同的解决方案，下面，我们介绍赛斯博瑞的基本想法。

二 塞斯博瑞解决绿蓝问题的想法以及两个反驳

在《悖论》一书中，塞斯博瑞较为详细的分析了这个问题，并提出了他自己的解决办法。他认为对绿蓝定义提出批评似乎意义不大；进而认为，问题似乎出在G1这条原则上，这条原则说的太少，过于宽泛，要避免绿蓝问题，必须加以限制。他分析道：根据绿蓝的定义，我们观察到的绿翡翠之所以是绿蓝的，仅仅是因为它们是被我们观察到了，如果它们没有被观察到，它们就不会是绿蓝的（因为在没有被观察到时若是绿蓝的，按绿蓝的定义，它们必须是蓝的）。为此，他给出如下原则：

（G2）：一个形式如“所有F都是G”的假说被它的一些示例所支持，当且仅当没有这样一个性质H，（1）使得证据中的所有F都是H，并且，（2）如果它们不是H的话，它们就不会是G。○1

举个例子，假设某个人只看到过煮过的龙虾，并作出假说所有的龙虾（F）都是粉红色（G）的。在这个例子中，有一个性质被煮过的（H），使得对这个人来说，他看到的龙虾（F）都是被煮过的（H），并且，如果它们没有被煮过（H），它们就不会是粉红色（G），而是暗红色的。由于上述条件H并满足G2的双蕴含式的右件的两个条件，因而根据G2，我们可以说，这个人的证据并不支持所有的龙虾都是粉红色的这个假说。

相似的，在绿蓝问题这个例子中，有一个性质，即被检查过的（H），使得证据中的（我们观察过的）翡翠（F）都是被检查过的（H），并且，如果它们没有被检查过（H），它们就不会是绿蓝色（G）。因为在没有被观察到时若是绿蓝的，按定义，它们必须是蓝的，而它们事实是绿的。同样，由于条件H满足G2的双蕴含式的右件的两个条件，因而根据G2，我们可以说，我们观察到的绿翡翠并不支持所有的翡翠都是绿蓝色的这个假说，进而也不会得出我们观察到的绿翡翠支持所有未检查的翡翠都是蓝色的这个假说。

到目前为止，一切令人满意。塞斯博瑞的基本想法是：是否存在这一个满足G2右件两个条件的性质，如果存在，我们就说证据不支持假说，反之，证据支持假说。我们也许可以画个图（见下图）来理解他的直观想法：令A代表所有检查过的翡翠（煮过的龙虾）；C代表所有绿的东西（所有的粉红色的东西）；D代表所有不是绿的东西（不是粉红色的东西）；B代表所有的翡翠（所有的龙虾）；B-C代表所有没有检查过的翡翠（没有煮过的龙虾）。这里满足G2的双蕴含式的右件两个条件的性质H可为：C与B的重叠部分。很明显，这个想法背后的直观很好，因为若不存在这样的H，那么似乎所有的B一定在A中。

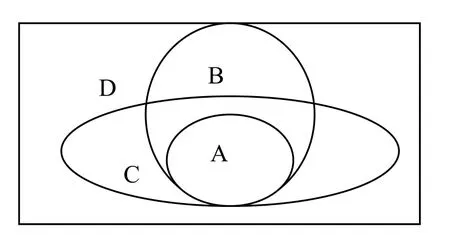
下面，我们给出两个反驳，这两个反驳表明，我们总能先天的找到一个满足G2右件两个条件的性质H，从而有：G2过于强大，以至于任何一个形式如“所有F都是G”的假说不能被它的任何示例（组）所支持。

第一个反驳很简单，（G2）说：一个形式如“所有F都是G”的假说被它的一些示例所支持，当且仅当没有这样一个性质H，使得证据中的所有F都是H，并且，如果它们不是H的话，它们就不会是G[1]P101。让我们假设一个假说所有F都是G是真的，事实上的确所有F（不管是过去的还是将来的）都是G。这样的话，我们只需令H为G即可，G本身就是一个满足G2右件两个条件的性质，从而我们可以说：即使对任何一个真的假说，一些“真正”支持它的证据，根据G2，我们也只能说证据不支持这个真的假说。

这个反驳很简单，也许人们说塞斯博瑞是不够仔细，我们可以退一步修改一下G2为：

（G2′）：一个形式如“所有F都是G”的假说被它的一些示例所支持，当且仅当没有这样一个性质H且H不是G，使得证据中的所有F都是H，并且，如果它们不是H的话，它们就不会是G。

接下来，我们给出第二个反驳，这个反驳表明：若使用如绿蓝一样的不自然的定义，我们总能先天的找到一个满足G2右件两个条件且不为G的性质H。让我们还以受此问题困扰的甲为例子，我们给甲几个定义，其中，蓝色与绿色使用绿蓝色和蓝绿色两种性质定义得出来的。定义如下：

蓝绿：X是蓝绿的当且仅当或者x是被检查过的并且它是蓝的，或者x是尚未检查过的并且它是绿色的。

绿色：X是绿的当且仅当或者x是被检查过的并且它是绿蓝的，或者x是尚未检查过的并且它是蓝绿色的。

蓝色：X是蓝色的当且仅当或者x是被检查过的并且它是蓝绿的，或者x是尚未检查过的并且它是绿蓝色的。

对于甲来说，甲观察到的绿翡翠因绿色的定义同时也是绿蓝色的。假设甲的假说是所有翡翠都是绿色的。甲想要得到结论：所有观察到的翡翠都是绿色的这些证据支持假说是所有翡翠都是绿色的。但是若我们使用上述利用蓝绿色与绿蓝色来定义绿色与蓝色的定义，我们总是能找到一个性质H，并且H满足G2′恒等式右件的两个条件。

我们的想法是：证据中所有翡翠都是绿色的，因其是绿色的，由绿色的定义，进而证据中所有翡翠同时也是绿蓝色的（证据中的翡翠都是检查过的），进而证据是所有翡翠都是绿蓝色的。相似的，有一个性质，即被检查过的（H），使得证据中的翡翠（F）都是被检查过的（H），并且，如果它们没有被检查过（H），它们就不会是绿色（G）（因为在没有被观察到时若是绿的，按定义，它们必须是蓝绿的，而它们事实是绿蓝的，当然，可以看出任何翡翠若是蓝绿色就不会是绿蓝色，反之也一样）。同样，由于上述找到的性质H满足G2′的双蕴含式右件的两个条件，因而根据G2′，甲可以说，甲观察到的绿翡翠并不支持所有的翡翠都是绿色的这个假说。

下面，我们用图来简单地加以解释（见下图）。按定义，我们不妨令A+B代表所有检查过的东西，C+D代表所有没有检查过的东西。A+D代表定义中绿色的东西，进而由定义，有A代表是绿蓝的检查过的东西，B是代表蓝绿色的未检查过的东西。不妨令E是检查过的绿蓝翡翠，F是所有的翡翠。令H为A+B即可。

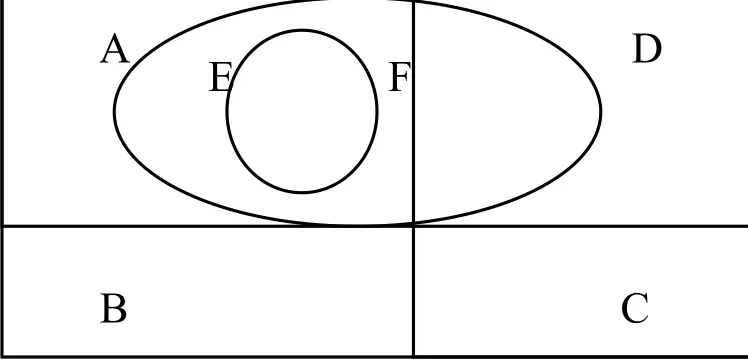
这样，即使所有的翡翠都是绿色的，由于我们能够找到一个一个条件H，满足G2′恒等式右件的两个条件，根据G2′，从而证据与假说之间的支持关系并不整理。对于这个反驳，我们可以说，我们只用到了一些不自然的定义与原则G2′，相比较于导致绿蓝问题的推理，我们的推理也不显得更为不合理。

三 结 语

到此为止，我们简单的叙述了绿蓝问题以及塞斯博瑞试图解决此问题的基本想法，并提出两个反驳。很明显，我们的第二个反驳如果是正确的话，那么这套办法很容易推广，从而使我们得到：在G2′这条原则下，任何证据都不会支持任何假说。而这个结论似乎是不可接受的，毕竟，我们是在寻找一种标准或原则，用来判别什么样的证据的确是支持某些结论的，而不符合标准的则不支持。另外，由于塞斯博瑞自己对G2似乎也并不满意，为此他相继给出了G3与G4。为了避免可能的简单反驳，我们在这里先说一点。不论塞斯博瑞的G3还是G4，他的基本想法都没有变化。他只是在考虑到事实上我们是否会知道有这样的H满足相应的条件，进而加上了“我们的证据并不显示存在这样的性质H”（G3），以及“我们的证据并不显示存在或很可能存在这样的性质H”这样的限制。而我们的反驳是：如果允许使用类似绿蓝这样稀奇古怪的定义，我们总可以先天地找出满足G2′恒等式右件的两个条件性质H，进而，这个反驳同样也可以适用于G3与G4。

由上可知，使用原则G1会使我们得到任何证据会支持任何假说的悖理结果；使用塞斯博瑞的原则G2，如果我们的反驳是正确的，会使我们得到任何证据都不会会支持任何假说的结果，也就是说，塞斯博瑞的G2过于强大，以至于把澡盆中的脏水与小孩一起都泼了出去。

注 释：

○

1原文如下：A Hypothesis “All F’s are G’s ” is confirmed by its instances if and only if there is no property H such that the F’s in the data are H , and if they had not been H , they would not have been G .(Sainsbury, R. M., Paradoxes, p101.)

[1]Sainsbury,R.M.Paradoxes[M].Cambridge University Press, 2009.

（责任编校：周 欣）

B81

A

1673-2219（2010）09-0095-03

2010―06―20

杨海波（1982―），内蒙古赤峰人，武汉大学哲学学院2006级博士生，研究方向为逻辑哲学。