基于广义子空间法的脑电诱发电位单导少次提取
王永轩 邱天爽 刘 蓉
(大连理工大学,电子信息与电气工程学部,大连 116024)
引言
脑电诱发电位(evoked potential,EP)是当对人的感官加以特定的刺激时,中枢神经系统所产生的有特定规律的生物电信号,它反映了相应的感觉通路及皮层区域的神经电活动情况,可以客观地评价人的感觉通路是否正常,是临床医学诊断神经系统损伤及病变的重要手段之一[1]。因为诱发电位是和自发脑电同时观测到的,所以必须先通过一定的方法提取出来。目前临床医学通常使用的方法是叠加平均法[1],也就是对感官进行多次刺激后,将每次记录的结果进行叠加平均。当刺激次数很大时,每次记录中的EP信号波形相差会变大,从而导致结果不可靠,另外当超出受试者的耐受力时会产生暴发伪迹,所以希望尽量减少刺激的次数,从而实现少次提取。
二十多年来,已经有很多研究者提出了许多不同的方法来提取EP信号,比如各种滤波法[2]、神经网络法[3]、小波分析法[4-5]、独立分量分析法[6]等。这些方法都有各自的特点,它们在解决各自的模型问题中都得到了很好的结果,但是这些方法所建立的模型应用于诱发电位单导少次提取问题中时有一定的局限性,所以无法真正应用到临床。比如独立分量分析法只能处理多导脑电信号,同时还要做很多假设,包括信号源必须是独立的,信号源数目要不多于观测信号路数,观测信号是信号源的线性混合,混和矩阵是列满秩的等等[7]。这些假设与实际并不完全相符,所以首先需要建立一个与实际问题尽可能相符的模型,然后再解决这个模型问题。
在所有的信号提取或信号增强问题中,人们都希望尽可能地去除或降低噪声而同时不破坏信号的完整性。只要运用得当,子空间法通常都可以很好地实现降低噪声与保留信号之间的折衷。因而子空间法不仅在脑电信号分析中,而且在功率谱估计[8]、系统辩识[9]和语音处理[10-11]等信号分析领域中都有着广泛的应用。例如Ephraim等人使用子空间法实现在白噪声背景中提取语音信号[10],而Rezayee等人进一步应用在有色噪声条件下同时并不需要对观测信号进行预白化[11]。基于EP信号与自发脑电相互独立这一性质,本研究提出了一种广义子空间法实现EP信号的单导少次提取。
1 广义子空间法
在单次刺激的情况下,EP信号是一段有限长的随机序列,令其为s(n),(n=1,2,…,N),令观测信号为x(n),(n=1,2,…,N),其中的自发脑电为v(n),(n=1,2,…,N)。将上述序列表示为向量,分别为s,x,v,则有x=s+v。
无论是经典滤波器还是现代滤波器,最终需要确定的都是由一组系数构成的序列,输出序列为输入序列与该系数序列的卷积,区别在确定这个系数序列所需的前提条件和准则不一样。因为序列可以用向量来表示,所以可以将它们统称为向量滤波器。而当待处理的信号为已记录的有限长的数据时,滤波器可以用一个矩阵来实现,称之为矩阵滤波器。如果用H表示矩阵滤波器,对于输入信号x,则有输出信号为y=Hx。y与期望信号s的误差为e=y-s=(H-I)s+Hv,均方误差为[10]

式(1)中误差自相关矩阵Re可表示为

其中Rs和Rv分别为信号和噪声的自相关矩阵,Rsv和Rvs分别为信号和噪声的互相关矩阵。由于EP信号与自发脑电是相互独立的,并且自发脑电在短时间内可以近似看作是零均值的平稳有色噪声,所以有Rsv=Rvs=0N×N,因此式(2)可简化为
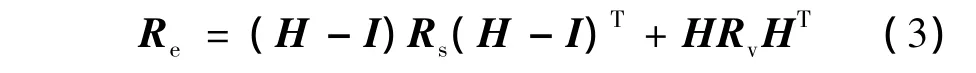
现寻求矩阵Hopt,使E(e2)达到最小,这样就可以得到EP信号在最小均方误差意义下的最佳估计=Hoptx。为了得到Hopt,需要先确定滤波矩阵H的基本结构。



若令T=[η1,η2,…,ηN],由双正交关系,可知[ξ1,ξ2,…,ξN]=T-T,则上述投影、加权和重构的过程可表达为=T-TDTTx。实际上信号和噪声所在的子空间不可能完全与线性无关,总会有相交的部分,这时可令D=diag(d),d=[d1,d2,…,dN]T,0≤di≤1。这种方法即为广义子空间法,由此可得滤波矩阵H的表达示为

其中T为投影矩阵,且为非奇异阵,其列向量是N维欧氏空间中的一组基;D为系数加权矩阵,且为对角阵,对投影系数进行加权;T-T为重构矩阵,其列向量是T的列向量的对偶基,从而组成双正交基。当T是正交阵时,有T=T-T,则T的列向量就是一组标准正交基。将式(6)带入式(3)中可得

在式(7)中同时出现了TTRsT和TTRvT,这相当于是用T同时对Rs和Rv进行合同变换。假设Rv是正定阵,现寻求投影矩阵Topt,使之可以实现Rs和Rv的同时合同对角化。由于Rs和Rv均为对称阵,所以可通过正交相似变换实现对角化,即

令

显然Rp是对称阵,又是非负定的,所以也可以通过正交相似变换实现对角化,且对角元素非负,即

定义投影矩阵Topt为

则Topt可以将Rs和Rv同时合同对角化为[12]
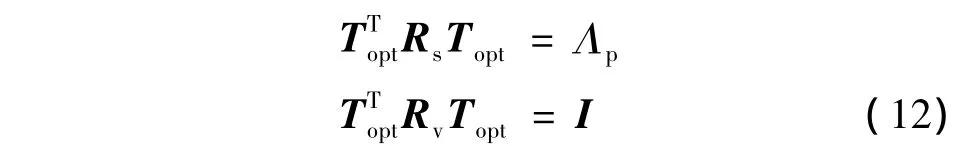
将式(7)、(12)代入式(1)中,可得

将E(e2)对di求偏导并置零,可得

由此可得系数加权矩阵Dopt为

在以上算法过程中,需要知道噪声自相关矩阵Rv和信号自相关矩阵Rs。Rv可由刺激前记录的观测信号(不包含诱发电位成分的纯净的自发脑电)计算得到。因为Rsv=Rvs=0N×N,所以有Rs=Rx-Rv,而观测信号自相关矩阵Rx可由观测信号计算得到。
2 仿真实验与分析
仿真实验中EP信号的来源为通过叠加平均法得到的猫的EP信号,采样频率为1kHz,单次EP信号存在时长为512ms。使用两个周期的EP信号(相当于两次刺激情况下的记录)令其为ss,即ss=[s(1),s(2),…,s(512),s(1),s(2),…,s(512)]T,将ss叠加上不同强度的有色噪声(对应不同的初始信噪比条件)做为观测信号xx=[x(1),x(2),…,x(1024)]T。观测信号自相关矩阵Rx由样本自相关矩阵近似代替,具体方法是首先由xx得到xi=[x(i),x(i+1),…,x(i+511)]T,(i=1,2,…,512),然后形成Hankel矩阵X=[x1,x2,…,x512]512×512,最后估计出观测信号的自相关矩阵Rx≈XTX/512。噪声自相关矩阵Rv可由不包含在xx中的噪声数据段计算得到。仿真实验使用的有色噪声的AR模型为[13]

其中w(n)为白噪声。式(16)的AR模型产生的有色噪声的有效频带为0~30Hz,峰值频率为13Hz,符合自发脑电的典型特征。而EP信号的有效频带为0~20Hz,峰值频率为10Hz,有色噪声在频带上完全覆盖了EP信号。在仿真实验中,初始信噪比(SNRi)由0dB逐渐降低到-10dB,衡量实验结果的指标为估计结果的归一化均方差(σ)、估计结果的信噪比(SNRo)和估计结果与纯净EP信号的相关系数(r)。

图1和图2分别为在SNRi=0dB和SNRi=-10dB条件下不同算法的估计结果。从实验结果可以看出,广义子空间法较好地抑制了噪声的干扰,使信噪比得到了很大程度的提高,在SNRi为-10dB时仍有较好的效果。在本文算法仿真实验中,使用了两个周期的EP信号(相当于两次刺激的情况),但估计结果比两次叠加平均的结果要好得多。
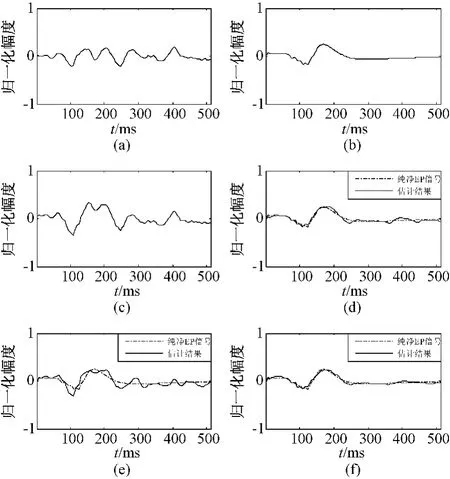
图1 不同算法在SNRi=0dB条件下估计结果的比较。(a)有色噪声;(b)纯净EP信号;(c)带噪信号;(d)子空间法估计结果;(e)两次叠加平均法估计结果;(f)子空间叠加平均法估计结果Fig.1 The comparison of the results estimated by different methods for EP signal(SNRi=0dB).(a)Colored noise;(b)Clean EP signal;(c)Noisy signal;(d)EP signal estimated by subspace method;(e)EP signal estimated by double average method;(f)EP signal estimated by subspace average method
图3、图4和图5分别为随着SNRi的降低,不同算法运行20次平均得到的σ、SNRo和r的变化情况。由图可见EP信号估计效果受制于信噪比。另外EP信号与噪声的相关程度也很重要,这是因为当相关程度较大时,就不能忽略信号和噪声的互相关,尽管EP信号与噪声的产生机理是独立的,但在时域表现上还会有一定的相关性。还有一个因素是噪声自相关矩阵和观测信号自相关矩阵的估计质量,更合理的估计方法会得到更好的效果。
3 结论

图2 不同算法在SNRi=-10dB条件下估计结果的比较。(a)有色噪声;(b)纯净EP信号;(c)带噪信号;(d)子空间法估计结果;(e)两次叠加平均法估计结果;(f)子空间叠加平均法估计结果Fig.2 The comparison of the results estimated by different methods for EP signal(SNRi=-10dB).(a)Colored noise;(b)Clean EP signal;(c)Noisy signal;(d)EP signal estimated by subspace method;(e)EP signal estimated by double average method;(f)EP signal estimated by subspace average method

图3 随着SNRi的降低,不同算法(子空间叠加平均法、子空间法、两次叠加平均法)得到的归一化均方差σ的变化情况。Fig.3 The relationship between normalized mean squared error σwith SNRifor different algorithms(subspace average method,subspace method and double average method)
本研究提出了一种广义子空间法用于脑电诱发电位单导少次提取,其核心是首先利用投影矩阵将信号和噪声同时投影到系数空间,再根据观测信号和噪声的自相关矩阵得到系数加权矩阵,对系数进行分离估计出信号的投影系数,最后利用重构矩阵进行重构得到期望的EP信号。该算法较好地抑制了自发脑电的干扰,使EP信号的信噪比获得了较大程度的提高。因为信号和噪声的频谱重叠,所以频谱分离法难以适用,而广义子空间法是根据观测信号构造投影矩阵,信号和噪声的投影系数可以同时非零,这样使算法的应用条件更加广泛。此外,与叠加平均法相比,该算法最少只需两次刺激得到的观测信号即可实现,大大减少了信号提取所需的周期。理论分析和试验结果均表明了该算法的有效性。我们将在下一步的研究工作中继续完善该算法,并将其应用于实际测试EP信号提取问题中。

图4 随着SNRi的降低,不同算法(子空间叠加平均法、子空间法、两次叠加平均法)得到的SNRo的变化情况Fig.4 The relationship between SNRowith SNRifor different algorithms(subspace average method,subspace method and double average method)
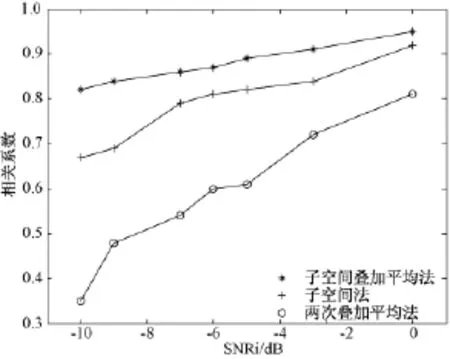
图5 随着SNRi的降低,不同算法(子空间叠加平均法、子空间法、两次叠加平均法)得到的相关系数r的变化情况Fig.5 The relationship between correlation coefficient r with SNRifor different algorithms(subspace average method,subspace method and double average method)
[1]潘映辅.临床诱发电位学(第2版)[M].北京:人民卫生出版社,2000.
[2]Stefanos DG,Perttu OR,Mika PT,et al.Single-trial dynamical estimation of event-related potentials:A kalman filter-based approach[J].IEEE Transactions on Biomedical Engineering,2005,52(8):1397-1406.
[3]Qiu Wei,Kenneth SM,Francis HY,et al.Adaptive filtering of evoked potentials with radial basis function neutral network prefilter[J].IEEE Transactions on Biomedical Engineering,2002,49(3):225-231.
[4]Wang Zhisong,Alexander M,David A,et al.Single-trial evoked potential estimation using wavelets[J].Computers in Biology and Medicine,2007,37(4):463-473.
[5]Quiroga R,Garcia H.Single-trial event-related potentials with wavelet denoising[J].Clin Neurophysiol,2003,114:376-390.
[6]毕晓辉,邱天爽,朱勇,等.基于经验模式分解和独立分量分析的单道少次EP信号提取[J].中国生物医学工程学报,2008,27(6):817-821.
[7]Aapo H,Erkki O.Independent component analysis:algorithms and applications[J].Neural Networks,2000,13(4-5):411-430.
[8]Kumaresan R,Tufts DW.Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise[J].IEEE Transaction on Acoustics,Speech and Signal Processing,1982,30(6):833-840.
[9]Overschee PV,Moor BD.Subspace Identification for Linear Systems[M].Boston:Kluwer Academic Publishers,1996.
[10]Ephraim Y,Trees HLV.A signal subspace approach for speech enhancement[J].IEEE Transactions on Speech and Audio Processing,1995,3(4):251-266.
[11]Rezayee A,Gazor S.An adaptive KLT approach for speech enhancement[J].IEEE Transactions on Speech and Audio Processing,2001,9(2):87-95.
[12]夏璇.二个矩阵同时对角化[J].南昌航空工业学院学报(自然科学版),2003,17(3):26-32.
[13]Yu Xiaohu,He Zhenya,Zhang Yisheng.Time-varying adaptive filters for evoked potential estimation[J].IEEE Transactions on Biomedical Engineering,1994,41(11):1062-1071.

