基于简比的C臂图像标记点自动匹配方法

孟 偲 张 军 吕绍杰 周晓君

（北京航空航天大学宇航学院，北京 100191）

引言

XRII（X-Ray Image Intensifier）C臂X光机（以下简称“C臂”）具有术中实时透视成像、移动方便和造价低廉的特点，广泛应用于医院临床诊断和手术导航。基于C臂图像的手术导航系统通过采用光学定位仪、C臂成像系统以及三维重构技术，可以实时获得患者的X光图像、手术工具、C臂之间的空间位置关系，从而直观、形象地辅助医生完成手术工具的精确定位及导向，可应用于骨科矫正、血管造影、起博器植入、栓塞介入等各类手术。基于C臂图像的图像导引手术系统（image guided surgery，IGS）已成为计算机辅助手术系统（computer aided surgery，CAS）的一个重要研究方向［1-4］。

C臂是将X射线源、影像增强器XRII分别集成在一个C形框架两端的X光成像设备。射线源发射出的X射线穿过成像对象，投影到影像增强器上，最终形成可见光图像［5］。受XRII的输入屏弧度、周边磁场、结构重量等因素的影响，其透视图像上不可避免地存在失真变形［6-8］，严重影响手术器械在图像上的定位精度［9］，因此利用C臂图像进行导航时必须对其进行校正。对C臂失真图像进行校正，关键在于建立C臂失真图像与理想图像对应像素之间的坐标转换关系及灰度值映射关系，然后利用该映射关系对失真图像进行校正。为了建立这种映射关系，一般需要采用专门的具有大量标记点的校准工具或模板。目前，国内外通常使用的校准模板一般采用高X线穿透率材料包埋低X线穿透率的金属球或金属板上密布小孔［11-12］，或金属丝组成的网格［3］，由金属球、小孔或网格的交点来形成标记点。标记点数目一般在100到数百不等，Soimu的研究表明，标记点越多，精度和效果会越好［13］。

基于C臂导航系统在进行手术器械定位时，需要对C臂的成像模型进行标定［10］。C臂标定方法类似于摄像机标定，需要通过标记点的世界坐标与图像坐标来标定模型。但在图像校正过程中，因为使用了大量的标记点，造成图像标记点与空间标记点自动对应的困难。另外，由于校准模板需要频繁拆卸、安装等原因，每次进入XRII视野中的标记点的位置和数量并不固定，这更增加了标记点自动对应的困难。目前，国内外在自动建立这种对应关系方面研究较少。钱理为等提出了一种基于标记点网格状态的自动校准模型算法［11］，利用最小生成树聚类算法区分不同类型的标记点，再利用基本顺序聚类算法建立相应的行列索引表及标记点查找表，进而自动建立标记点世界坐标与图像坐标的对应关系。该方法能实现标记点的自动匹配，但算法较为复杂。黄惠芳等提出一种网格点标记编号方法，可以处理进入XRII视野标记点变化的问题［3］，但算法复杂且没有研究与空间位置对应的问题。

针对C臂图像校正与系统标定过程中存在大量标记点需要自动对应的问题，笔者提出一种基于简比仿射不变量的标记点图像坐标与空间坐标自动对应方法。首先，在自行设计的双层校准模板的底层模板上，制作3个大的标记点，以在校准模板及其C臂图像上建立仿射坐标系；其次，通过建立平面单应关系，将利用形态学方法提取出的校准模板的标记点图像坐标转换为仿射坐标；然后，利用简比为仿射变换不变量性质，将图像仿射坐标归整，实现与校准模板标记点的自动对应；最后利用标记点投影性质区分上下两层标记点，并消除因投影失真产生的错误对应，从而实现了标记点图像坐标与空间点坐标的自动准确对应。大量的测试试验表明，该方法稳定性好、鲁棒性强，具有实现简单、无需人工介入等优点，可应用于基于C臂X光图像的手术导航系统中。

1 基于简比的标记点自动匹配原理

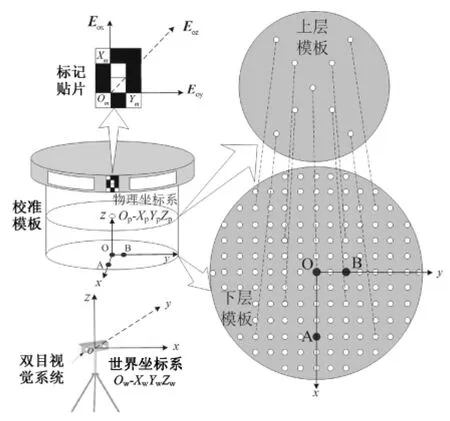
图1 校准模板示意（黑色点代表大点，白色点代表小点）Fig.1 Calibration template（black for big points，white for small points）

为完成C臂标定，设计制作了一款双层校准模板。模板采用铝制双层薄板挖孔结构，圆孔按照等间距、有规律的方式排列（见图1）。该模板设计为上、下两层，使用时固定在C臂影像增强器上。其中，远离影像增强器的一层为下层模板，在下层模板上等间距（20mm）均布了128个标记点，上层模板分布了9个标记点，分别与下层9个位置的标记点垂直对应（见图1）。为了能在校准模板及其X光图像上识别标记点顺序，在下层模板中心位置特制了3个大标记点，分别是图1中的点O、A、B；OA长80mm，OB长40mm，且OA⊥OB。在校准模板上，可利用这3个大点建立物理坐标系Op-XpYpZp，以区分模板上的标记点，该坐标系以标记点相对于原点的实际物理距离表示点的位置。为了获取标记点的世界坐标，需要在校准模板的边缘贴标记贴片（如图1所示），该贴片上有3个Mark点。在进行系统导航时，双目视觉系统会建立一个世界坐标系Ow-XwYwZw，并可实时获取贴片中点Om、Xm、Ym的世界坐标，由模板半径等自身参数，亦可获取此3点在物理坐标系下的坐标，由此可建立两种坐标系的转换关系。

C臂光源发射出X线将校准模板投影到影像增强器并形成X光图像，该成像过程为中心透视射影变换。由射影变换理论可知，当射影中心趋向无穷远时的射影变换近似为仿射变换。由于校准模板安装在XRII上，故模板到成像面的距离远小于源像距（source image distance，SID），从校准模板到影像增强器的射影变换近似为仿射变换。因此，在校准模板上以物理坐标系Op-XpYpZp的x、y轴构成的二维坐标系（如图1所示）投影到X光图像中将成为仿射坐标系Oa-XaYa（如图3所示）。平面仿射坐标系由相交于O点的任意两条直线及其方向、平面上不在两条直线上的单位点E定义，即仿射坐标系下点的坐标为简比坐标。X光图像中的仿射坐标系Oa-XaYa，以直线O′A′作x轴、直线O′B′作y轴，点M′作为单位点。仿射变换会保持校准模板与其X光图像间共线3点的简比不变，因此在理想情况下，标记点在物理坐标系Op-XpYpZp下的x、y坐标与仿射坐标系Oa-XaYa下的简比相等，这就建立了图像点与空间点的对应。利用标记点的仿射坐标乘以点间的实际物理距离即可获得点的物理坐标，同时利用标记贴片上点Om、Xm、Ym的世界坐标及其在物理坐标系下的坐标可获取Ow-XwYwZw、Op-XpYpZp之间的转换关系。因此，最终可建立仿射坐标系与世界坐标系的转换关系，由标记点的仿射坐标即可获得其世界坐标（见图2）。

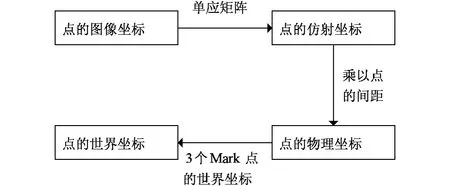
图2 坐标系之间的转换关系Fig.2 Transformation between coordinate systems

2 标记点自动匹配算法

针对C臂标定过程中图像标记点与空间标记点的自动对应问题，提出了一种基于简比的标记点图像坐标与世界坐标的自动对应方法。在理想情况下，标记点在仿射坐标系以及物理坐标系下的简比相同，由此，可建立图像点与空间点的对应关系。

2.1 自动提取X光图像中的标记点

基于形态学的标记点自动提取方法［11-12］，是C臂图像校准模板中提取标记点的通用方法，采用形态学的方法进行标记点自动识别和提取。首先利用维纳滤波对图像进行去噪处理，之后使用开运算获取模板背景图，然后用原始图减去背景图获得目标图，再进行阈值分割，提取标记点区域。经过以上步骤后，可得到标记点的质心坐标。通过形态学方法，自动提取出n个标记点的质心坐标为（xi，yi），（i=1，2，…，n）。

2.2 确定图像中3个大标记点的位置

为了能够利用X光图像中3个大标记点的投影来建立仿射坐标系，必须确定这3个点的绝对位置。首先，遍历整个二值化图像中所有标记点，找出面积最大的3个标记点。此3点两两之间可组成3条直线，每条直线可以确定出一个方向向量，计算两两向量的夹角，最大夹角所对应的点即为中心大标记点的投影。

然后，计算另外两个大标记点的投影点到中心点的距离dO′A′，dO′B′（dO′A′＞dO′B′）。这里，设离点O′较远点的齐次坐标为A′（xA′，yA′，1）T，较近点的齐次坐标为B′（xB′，yB′，1）T。

2.3 建立仿射坐标系

确定出模板X光图像中3个大标记点的位置后，即可建立仿射坐标系。如图3所示，以O′为原点，点O′与点A′确定的直线为x轴、点O′与点B′确定的直线为y轴。由于校准模板上的标记点是等间距dE分布，且dO′A′=4dE、dO′B′=2dE，因此以dE为坐标轴单位长度。至此，可建立仿射坐标系Oa-XaYa。

2.4 计算标记点的仿射坐标

仿射坐标系Oa-XaYa建立后，可以利用单应矩阵求取标记点的仿射坐标。在理想情况下，各标记点在Oa-XaYa下的简比坐标应为整数，但由于C臂图像存在失真，简比不一定为整。因此，在求取各标记点的简比坐标后需要进行归整处理。

单应矩阵可以建立起两个平面射影变换的对应关系。为了确定单应矩阵，需要从X光图像中选取4个点，且这4个点中任意3点不共线，因此可选取点O′、A′、B′及点M′（见图3）这4点。利用形态学方法可自动提取出此4点的图像坐标，分别记作O′=（xO′，yO′，1）T，A′=（xA′，yA′，1）T，B′=（xB′，yB′，1）T，M′=（xM′，yM′，1）T；其对应的仿射坐标系下的齐次坐标为Oa=（0，0，1）T，Aa=（4，0，1）T，Ba=（0，2，1）T，Ma=（1，1，1）T。利用此4点的图像坐标及其仿射坐标构造出4个点对应，由此可计算出从图像坐标系投影到仿射坐标系的单应矩阵H。

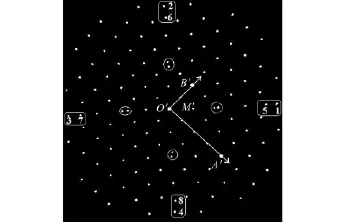
图3 校准模板X光图像的二值化图Fig.3 Binary image of calibration target X-ray image

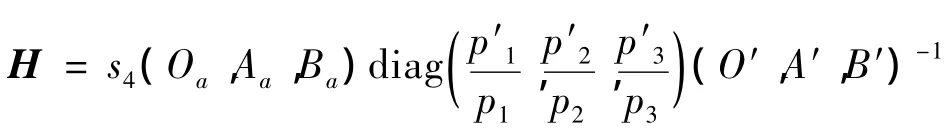
式中，（p1，p2，p3）T=（O′，A′，B′）-1M，（p′1，p′2，p′3）T=（Oa，Aa，Ba）-1Ma。

通过单应矩阵H，可由标记点的图像坐标（xi，yi，1）T计算出其仿射坐标的齐次坐标为（xai，yai，1）T。

（xai，yai，1）T=H（xi，yi，1）T

由此获得的仿射坐标不一定为整数，需要对其进行归整处理，标记点归整后的仿射坐标记为（［xai］，［yai］，1）T。

2.5 分离上下两层模板标记点

由于标记板是双层结构，而X光图像并不能显示标记点的深度信息，为了正确求取标记点的世界坐标，需要分离上下两层模板标记点在图像中的投影。

校准模板上层有9个标记点，下层有128个标记点。在安装校准模板时，尽量使上下两层模板的中心大标记点平行于C臂光源与影像增强器的轴心，以保证上、下两层的中心点在X光图像中的投影重叠，因此只需要将上层模板的8个标记点找到即可。而上层模板离影像增强器更近，所以两层模板同一位置的标记点（除中心大标记点）在X光图像中的投影到中心点距离不同，表现为上层标记点投影位置距离中心点更近（如图4所示）。因而，可利用此性质分离上下两层标记点。

在理想情况下，上层模板标记点的横、纵坐标应相等且绝对值都为2（或4）。在实际操作中发现，由于X光图像存在失真，上层标记点不一定全部满足这种规律，而下层模板所对应的标记点满足此规律。因此，先找到仿射坐标系下横、纵坐标绝对值均为2（或4）的标记点，这些点中距离点O最远的4点为下层模板的标记点，因而离此4点最近的点即为上层模板的标记点。在横、纵坐标绝对值均为2或4的点中利用上述方法，最终可以确定出上层模板的8个标记点。

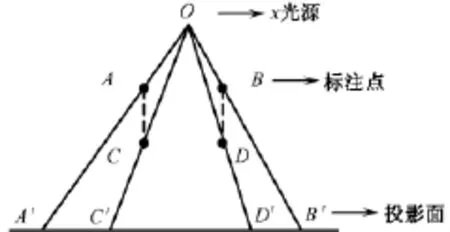
图4 上下两层模板标记点投影示意Fig.4 Projection of markers on upper and lower template

2.6 实现图像坐标与世界坐标的对应

由双目视觉系统可以获取标记贴片上3个Mark点的世界坐标，分别记作Om（x1，y1，z1）、Xm（x2，y2，z2）、Ym（x3，y3，z3），通过这3点坐标可确定出3个单位向量Eox、Eoy、Eoz（见图1）。

OXm=（x2-x1，y2-y1，z2-z1），OYm=（x3-x1，y3-y1，z3-z1）

Eox=OXm/|OXm|，Eoy=OYm/|OYm|，Eoz=cross（Eox，Eoy）

式中，cross表示向量叉乘，| |表示向量的模。

此外，利用校准模板设计所用的参数，可以获得下层模板中心标记点沿Eox、Eoy、Eoz方向到标记贴片的距离d1、d2、d3，因此下层模板中心点在世界坐标系下的坐标为

Ob=Om+d1Eox+d2Eoy+d3Eoz（Ob为下层模板中心点的世界坐标）

物理坐标系Op-XpYpZp的x轴与向量Eoz平行且方向相反，y轴与向量Eoy平行且方向相同，z轴与向量Eox平行且方向相同，又已知下层模板中心点的世界坐标，由此可计算出模板各标记点的世界坐标：

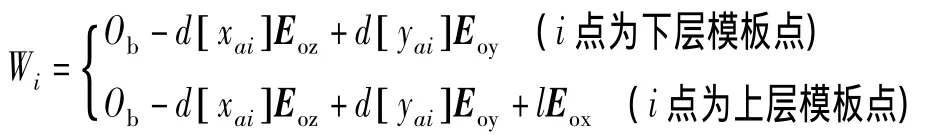
式中，Wi为仿射坐标系中点I（［xai］，［yai］，1）T的世界坐标，d为模板相邻两标记点之间的实际物理距离，l为上下两层模板的距离。

通过以上步骤，最终可完成标记点图像坐标系与世界坐标系的自动对应。

3 试验验证与结果

为了对上文阐述的C臂图像标记点自动对应方法进行验证，笔者利用Matlab7.4对算法进行了编程实现，试验所用X光图像分辨率为512像素×512像素。

基于C臂图像的手术导航系统，在进行手术器械定位时，一般采用C臂位于正位、侧位时获取的同一病灶部位的两幅或多幅X光图像进行三维重建。本研究利用海军总医院介入室的C臂，获取了多幅校准模板的图像。将C臂仰角固定为0°，在倾角范围［-90°，90°］内，以5°为间隔，采集了多幅校准模板的X光图像，并利用本研究提出的算法，对这些存在失真的X光图像进行了标记点匹配试验。试验表明，算法能正确处理所有的校准模板图像。

选取C臂位于正位（倾角为0°）时的校准模板图像（如图6（a）所示）进行重点说明。首先，利用形态学方法提取出的点O′、A′、B′、M′图像坐标的齐次坐标分别为

O′=（249.178 6 258.357 1 1）T

A′=（361.755 1 361.081 6 1）T

B′=（298.840 0 206.260 0 1）T

M′=（300.653 8 257.6538 1）T

利用此4点的图像坐标与其对应的理想仿射坐标，可以得到单应矩阵为

通过计算得到的单应矩阵H，利用标记点的图像坐标，可以计算出标记点对应的仿射坐标（见图5）。图中，*表示坐标归整值无误的点，△表示坐标归整值有误的点。利用第2节的算法，通过对计算出的仿射坐标计算值进行归整、修正，可以成功匹配X光图像中所有标记点。但是，由于图像中标记点个数太多，在此只选取有代表性的12个点逐一说明。这些点包括：点O′、A′、B′、M′，上层模板外围4点及其对应的下层模板4点（见图3）。

图5 标记点仿射坐标计算值示意图（*为归整值无误的点，△为归整值有误的点）Fig.5 The calculated value of affine coordinates（*for correct rounding value，△for incorrect rounding value）

由表1可知，利用单应矩阵直接计算出的仿射坐标不一定为整数，对原始计算值进行归整后，下层模板标记点的坐标都是正确的，上层模板4点中有些点（编号为7和8的点）是错误的。因此，需要利用第2节中的方法对上层模板标记点坐标进行修正，通过该步修正后即可获得正确的仿射坐标。

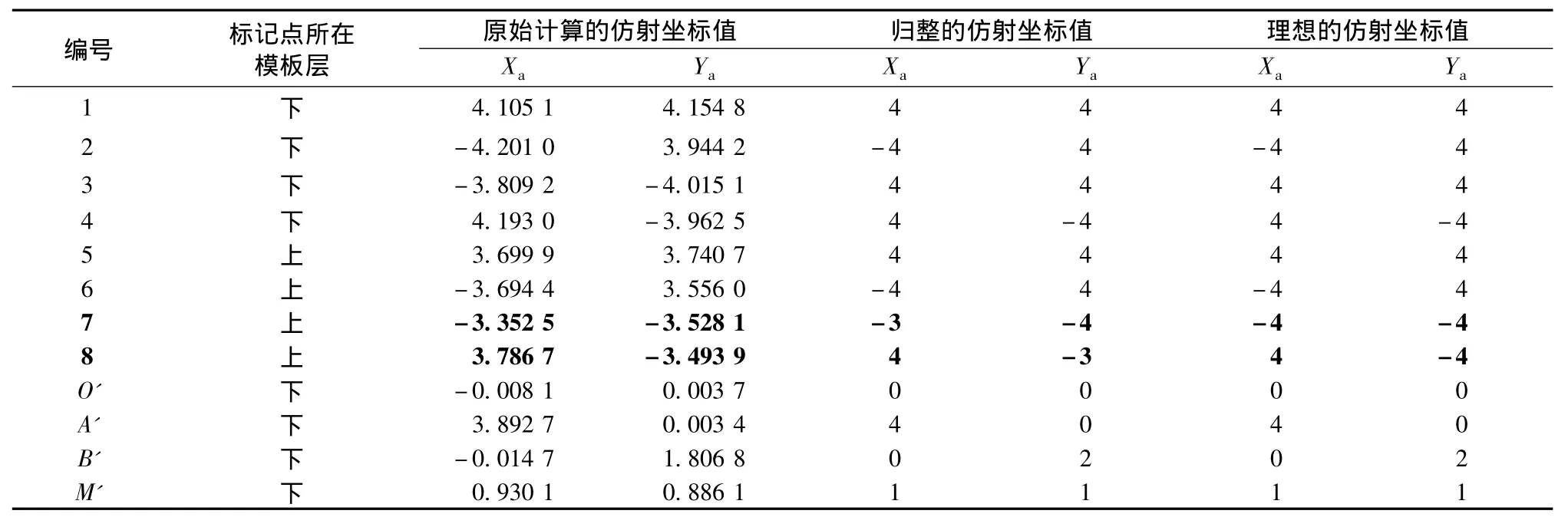
表1 仿射坐标的计算值、归整值、理想值比较（粗体字为归整坐标错误的点）Tab.1 The calculated value，rounding value，ideal value of affine coordinates（bold for points with wrong rounding value）

获得正确的标记点仿射坐标后，即可利用上述方法获取标记点的世界坐标。试验发现，利用基于简比的标记点自动匹配方法，能够正确建立校准模板标记点图像坐标与世界坐标的对应关系；对于安装时经水平仪校正和未经水平仪校正的模板（见图6），都能顺利完成对应关系的自动建立，所得结果稳定、效果理想，能满足后续工作的需求。

图6 标记点对应关系试验。（a）未经校正安装的模板X光图；（b）标记点图像坐标图；（c）标记点世界坐标三维图Fig.6 Correspondence relationship of markers.（a）X-ray image；（b）image coordinate；（c）world coordinate

4 讨论和结论

通过研究分析基于C臂的手术辅助系统中标定C臂时存在的问题，提出了一种基于简比的C臂图像标记点的自动匹配方法。该方法采用形态学方法，自动识别、提取标记点的图像坐标，利用射影几何等相关理论，依次建立了标记点的图像坐标、仿射坐标、物理坐标、世界坐标之间的转换关系，最终可自动建立校准模板标记点图像坐标与世界坐标的对应关系。

大量的测试试验证明，该方法无需校正失真的X光图像，即可在短时间内实现对校准模板标记点图像坐标与世界坐标对应关系的自动建立，具有实现简单、稳定性好、鲁棒性强、无需人工介入等优点，简化了标记点两种坐标对应步骤，大大缩短了标定C臂所需时间，对于提高C臂标定的精度和手术效率、减少病人痛苦具有实用价值。目前，该方法现已成功应用到海军总医院介入室的动物临床试验中。

［1］Marwan S，Hans U，Staubli M D，et al.Clinical integration of computer-assisted technology for arthroscopic anterior cruciate ligament reconstruction［J］.Operative techniques in orthopaedics，2000，10（1）：40-49.

［2］刘文勇，王满宜，王田苗，等.计算机辅助髓内钉远端锁定系统误差分析［J］.北京航空航天大学学报，2004，30（9）：850-854.

［3］黄惠芳，张璞.基于形态学和多项式的数字减影血管造影图像几何失真的校正［J］.生物医学工程研究，2008，27（1）：31-35.

［4］Sati M，St¨aubli HU，Bouquin Y，et al.Real-time computerized in situ guidance system for ACL graft placement［J］.Computer Assisted Surgery，2002，7（1）：25-40.

［5］金玉博.医用X射线影像增强器的原理和检测［J］.中外医疗，2008，27（21）：165-166.

［6］Forlani C，Ferrigno G.Automatic real-time XRII local distortion correction method for digital linear tomography［A］.In：Alexandrov VN，eds.Proceedings of International Conference on Computational Science［C］.Heidelberg：Springer Berlin，2001.23-26.

［7］Cerveri P，Forlani C，Borghese NA.Distortion correction for x-ray image intensifiers：Local unwarping polynomials and RBF neural networks［J］.Medical Physics，2002，29（8）：1759-1771.

［8］Gronenschild E.Correction for geometric image distortion in the xray image chain：local technique versus global technique［J］.Medical Physics，1999，26（12）：2602-2616.

［9］Slomczykowski M，Hofstetter R，Strauss M，et al.Fluoroscopybased surgical navigation-concept and possible clinical applications［A］.In：Nolte LP，Ganz R，eds.Computer Assisted Orthopedic Surgery［C］.Bern：Hogrefe and Huber Publishers，1999.206-217.

［10］Livyatan H，Yaniv Z，Joskowicz L.Robust automatic C-arm calibration for fluoroscopy-based navigation：A practical approach［A］.In：Dohi T，Kikinis R，eds.Fifth International Conference on Medical Image Computing and Computer-Assisted Intervention［C］.Piscataway：IEEE Press，2002.60-68.

［11］钱理为，王成焘，闫士举，等.基于校准靶的C形臂相机模型自动校准方法［J］.计算机工程，2009，35（15）：7-9.

［12］王田苗，刘文勇，胡磊，等.基于多项式拟合的C臂投影全局校正法［J］.高技术通讯，2007，17（9）：919-922.

［13］Soimu D，Badea C，Pallikarakis N.A novel approach for distortion correction for X-ray image intensifiers［J］.Computerized Medical Imaging and Graphics，2003，27（1）：79-85.