非单调信息下的随机微分效用

任欢

（安阳工学院 数理系，河南 安阳 455000）

非单调信息下的随机微分效用

任欢

（安阳工学院 数理系，河南 安阳 455000）

本文通过倒向重随机微分方程引入了一类非单调信息下的随机微分效用，讨论其解的唯一性及连续性，关于终值的单调性以及关于消费的单调性.

倒向重随机微分方程；随机微分效用；效用函数；解的存在唯一性；比较定理

1992年，D u f f i e和E p s t e i n[1]定义了消费过程C的效用过程为一半鞅（V t)0≤t≤T，满足I t o赞型随机微分方程Vs)ds|Ft]，或写成倒向随机微分方程（简称B S D E）的形式:，其中F由布朗运动生成，是一个经典的信息流.1994年，P a r d o u x和P e n g[2]提出一类新型的B S D E——倒向重随机微分方程（简称B D S D E s）:

这里关于{Bt}的积分是倒向I t o赞积分，关于{Wt}的积分是标准正向I t o赞积分，这两种积分是I t o赞-S k o r o h o d积分的特殊类型（见文献[3]），其中{Ft:0≤t≤T}既非单调增也非单调减，因而不构成一个信息流.本文受到以上文献的启发，引入了非单调信息下的随机微分效用.

1 预备知识

对任意的向量x∈Rk和A∈Rd×k，记其欧几里德范数分别为|x|和||A||:=T r A A*姨 ，其中A*表示A的转置.

给定概率空间(Ω,F,P)，T≥0为一固定时间常数.{Wt;0≤t≤T}和{Bt;0≤t≤T}是定义于(Ω,F,P)上的两个相互独立的标准布朗运动，分别取值于Rd和Rt.令N表示F中P-零集构成的集合.对于每一个t∈[0,T]，定义F t:=Fwt∨FBt,T，对任意的随机过程{ηt}，Fηs,t=σ{ηr-ηs;s≤r≤t}∨N，Fη

t=Fη

0,t.显然{Ft;0≤t≤T}既非单调增也非单调减，因而不构成一个信息流.

对于任意的自然数n∈N，记M2{0,T;Rn)={φ:φt为n维联合可测(d P茚d t)的随机过程，且对于几乎每个t∈[0,T]，φt为Ft-可测}.

令f:Ω×[0,T]×Rk×Rk×d→Rk,g:Ω×[0,T]×Rk×Rk×d→Rk×l均联合可测，假设：

（H 1）f(·,y,z)∈M2(0,T;Rk)，f(·,y,z)∈M2(0,T;Rk×l)；

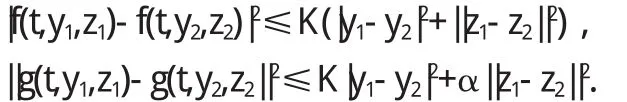
（H 2）对任意的(ω，t)∈Ω×[0,T]，(y1,z1),(y2,z2)∈Rk×Rk×d,埚K>0,0<α<1，有，对于几乎每个t∈[0,T]，φt为Ft-可测}，S2([0,T];Rn)={φ:φt为n维连续随机过程，且引理1.1[2]令α∈S2([0,T];Rk),β∈M2(0,T;Rk)，γ∈M2(0,T;Rk×l), δ∈M2(0,T;Rk×d)满足：

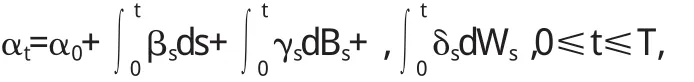
则

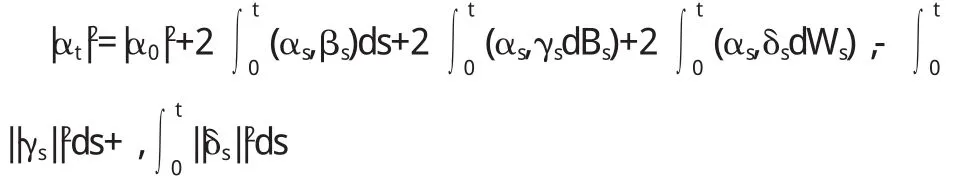
引理1.2[2]给定ξ∈L2(Ω,FT,P;Rk)(，假定f,g满足条件（H 1）（H 2），则存在唯一一对过程(Y,Z)∈S2([0,T];Rk×M2(0,T; Rk×d)为方程（1.1）的解.

引理1.3[4]（比较定理）假设f1,f2和g满足（H 1）（H 2），若k=1时，有ξ1≥ξ2，a.s.，f1(t,y,z)≥f2(t,y,z)，a.s.,坌(t,y,z)∈[0,T] ×R×Rd，则坌t∈[0,T]，Y1t≥Y2t，a.s.，其中(Y1,Z1)和(Y2,Z2)分别为下列B D S D E s方程的解：

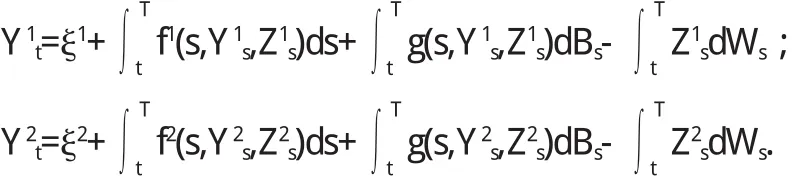
2 定义

下面给出本文采用的符号.

记L2F{(Ω,FT,P;Rn)={ξ:ξ为FT-循序可测的n维随机变量，且E|ξ|2<∞}，M2F(0,T;Rn)={φ:φt为n维联合可测(d P茚d t)的随机过程，且，对于几乎每个t∈[0,T]，φt为Ft-循序可测}([0,T];Rn)={φ:φt为n维连续随机过程，且E，其中|C|表示某一消费过程C∈C的范数.

假设F:Ω×[0,T]×R×R×Rd→R，G:Ω×[0,T]×R×Rd→Rl是联合可测的，且满足：

（H 3）F(·,Cl,V,Z)∈M2F(t,O,T,R)，G（·，V，Z）∈M2F(O,T;Rl)，对于几乎每个t∈[0,T]，φt为Ft-循序可测}.

消费过程C={Ct}取值于某个可分B a n a c h格中的闭凸子集C.消费过程集合D为C值平方可积循序过程全体，记C在D中的范数为（H 4）对任意的(ω,t)∈Ω×[0,T]，(V1,Z1),(V2,Z2)∈R×Rd，存在常数K>0,0<α<1，有

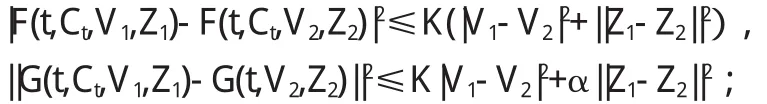
（H 5）F关于消费C满足线性增长条件：对任意的C∈R，存在常数K1,K2>0，使得

定义2.1给定ξ∈L2F(Ω,FT,P;R)及消费过程C∈D，假设F和G满足条件（H 3）-（H 5），若存在(V,Z)∈S2F([0,T];T)× M2F(0,T;Rd),a.s.满足：

则称(Vt)为消费过程C的递归效用过程；称V0为消费过程C的递归效用.

若映射U:D→R，使得U(C)=V0，则称U为递归效用函数.

3 定理及性质

定理3.1（解得存在唯一性）给定ξ∈L2F(Ω,FT,P;R)及消费过程C∈D，假定F,G满足条件(H 3)-(H 5)，则方程（1.2）存在唯一的解(V,Z)∈S2F([0,T];R)×M2F(0,T;Rd).

证明 参照引理1.2的证明即可得出结论.

定理3.2（比较定理）假设F,G满足(H 3)-(H 5)，设(Vt,Zt)是方程（1.2）的解，(V,Z)满足

证明令f1(t,Vt,Zt)=F(t,Ct,Vt,Zt)，f2(t,Vt,Zt)=F(t,Ct,Vt,Zt)，则

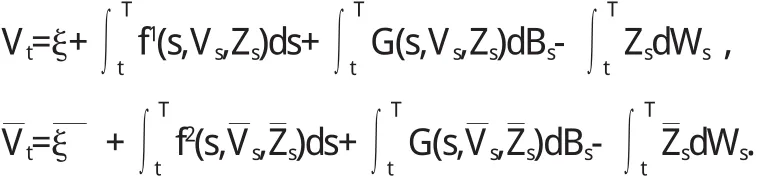
由定理条件知，ξ≥ξ，f1(t,Vt,Zt)≥f2(t,Vt,Zt)，利用引理1.3可得：

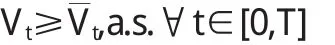
性质3.3（连续性）若F是连续函数，则效用函数U:D→R是连续的.

证明 设消费过程列{Cn}在D中收敛到C，即E

记{Cn},C对应的效用过程分别为Vn=VCn,V=VC.对任意t∈[0,T]，有

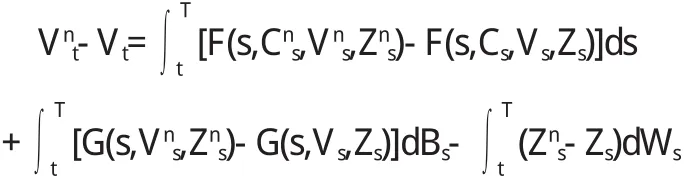
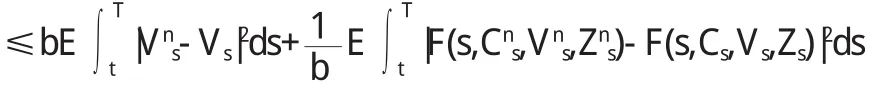
因为2 E

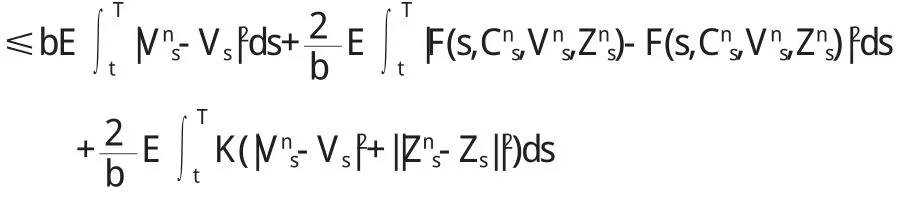
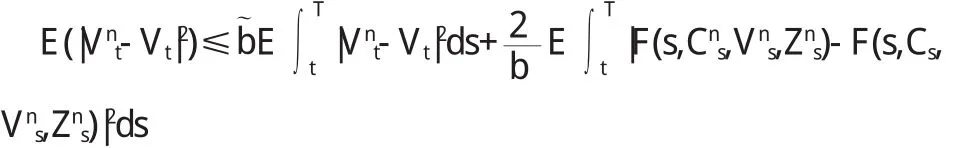
由G r o n m a l l—B e l l m a n不等式得：坌t∈[0,T].特别当t=0时，有

性质3.4（关于终值的单调性）若ξ1,ξ2∈L2F(Ω,FT,P;R)且

证明 由定理3.2可直接得结论.

性质3.5（关于消费的单调性）若F为消费过程C的递增函数，则U为C的递增函数；若F为消费过程C的严格递增函数，则U为C的严格递增函数.

〔1〕DuffieD，Epstein L G.Stochasticdifferentialutility[J].Econometrica，1992，60(2)：353-394.

〔2〕Pardoux E，Peng S.Backward doubly stochastic differential equations and systems of quasilinear parabolic SPDE’s[J].Probab Theory Related Fields，1994，98(2)：209-227.

〔3〕Nualart D，Pardoux E.Stochastic calculus with anticipating intergrands[J].Probab Theory Related Fields，1988，78(4)：535-581.

〔4〕Shi Y，Gu Y，Liu K.Comparison theorem of backward doubly stochastic differential equations and applications[J].Stochastic Analysis and Applications，2005，23(1)：1-14.

〔5〕周少甫，王湘君.非-Lipschitz条件下随机微分效用[J].华中科技大学学报，1999，27(11)：101-103.

O 175

A

1673-260X（2010）07-0004-02