振动筛机架结构的优化设计

张卡德，黄致建，郝艳华

（华侨大学机电及自动化学院，福建 泉州 362021）

振动筛机架结构的优化设计

张卡德，黄致建，郝艳华

（华侨大学机电及自动化学院，福建 泉州 362021）

建立振动筛机架的有限元模型和优化模型，对刚度、强度和稳定性储备量足够大的振动筛机架进行优化设计.把设计变量的尺寸规格值作为优化后最优值，对优化后振动筛机架进行刚度、强度和稳定性校核.结果表明，经过优化后的振动筛机架的总质量有显著的降低，减小了29.41％；刚度、强度都满足设计要求，优化后振动筛机架不会出现失稳现象，结构稳定性好.

振动筛机架；优化设计；强度；刚度；稳定性

振动筛是对物料按粒径进行分级的专用设备.近年来，许多搅拌设备产品采用振动筛对砂粒进行分级，以达到生产高效的目的.由于材料的成本不断提高，各行业都希望其产品在满足要求下，能尽量地节约能源和材料的成本.振动筛主要由机架、弹簧、筛箱组成.振动筛机架是通过弹簧来支撑筛箱的上下振动，振动筛机架的刚度、强度和稳定性直接关系到筛箱工作的可靠性.本文应用有限元软件ANSYS对振动筛机架进行优化设计，并对优化后振动筛机架的刚度、强度和稳定性进行校核.

1 优化模型的建立

在振动筛机架的优化计算前，要建立正确和合理的有限元模型（图1）和优化模型.优化模型包括目标函数、设计变量和约束条件［1］.对于复杂的结构，优化模型的参数很多，手工定义相当繁琐.因此，利用有限元软件ANSYS的优化功能［2］，使优化模型的建立和优化结果的后处理变得方便.

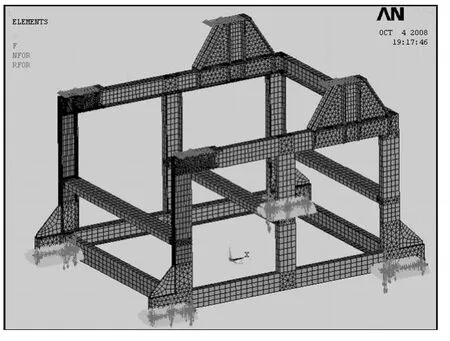
图1 振动筛机架有限元模型Fig.1 Finite element model of vibrating screen frame

1.1 目标函数

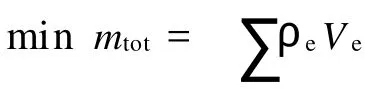
1.2 设计变量

振动筛机架的设计变量，取槽钢截面的厚度（x1）、加强筋的厚度（x2）、垫板的厚度（x3）和固定板的厚度（x4），以及槽钢截面的长（x5）和宽（x6）.设计变量x1～x6的初值分别为9，12，16，20，200，75mm，而它们的约束范围：6.5mm≤x1≤9mm；6mm≤x2≤12mm；10mm≤x3≤16mm；12mm≤x4≤20mm；178mm≤x5≤200mm；65mm≤x6≤75mm.

1.3 约束条件

状态变量是根据设计对象应满足的功能要求而建立的约束条件.对于结构优化问题，约束条件主要考虑对结构强度、刚度及稳定性应满足的要求.对于振动筛机架，主要的要求是刚度.一般来说，刚度达到要求，强度也能满足要求.振动筛机架的约束条件：Xmin≥-0.9mm；Xmax≤0.9mm；Ymin≥-1.0mm；Ymax≤1.0mm；Zmin≥-0.6mm；Zmax≤0.6mm.

2 振动筛机架的优化分析结果

振动筛机架目标函数、设计变量和约束变量随着迭代次数（n）的变化情况，如图2所示.从图2（a）可以看出，迭代到16步后，机架的总质量mtot基本保持不变，迭代到24步才达到收敛的容差0.000 1，并取得最优值为742.04kg.

图2 优化参数随迭代次数的变化情况Fig.2 Variations of optimization parameters with the number of iterations

振动筛机架设计变量和状态变量的初值、最优值的对比，如表1所示.从表1可知，当目标函数达到最小值时，各设计变量的最优值不符合材料实际的尺寸规格值，但可以取与最优值最接近的材料尺寸规格值.当设计变量取材料尺寸规格值，即x1～x6的值分别为7.0，10，10.5，12，180，68mm时，材料的刚度、强度和稳定性都有所变化.

表1 振动筛机架设计变量与状态变量的对比Tab.1 Design bariables contrast with the state variables of vibrating screen frame mm

3 优化后振动筛机架的结构校核

3.1 振动筛机架边界条件

在振动筛机架的固定板上施加所有的自由度.在静强度分析中，机架受到是筛箱和砂子的压力，每个支撑点受到的压力为4.250kN.在动强度分析中，机架受到两种周期性交变载荷，如图3所示.一种是振动筛激振力所产生的水平分力作用在振动筛机架的8个支座上；另一种是筛箱在振幅为3mm的范围内的振动.压力的变化也就是周期性交变载荷.

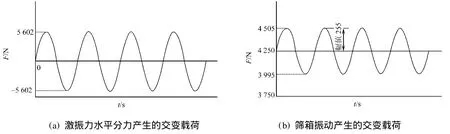
图3 振动筛机架所受的周期性交变载荷Fig.3 Periodical changing load of vibrating screen frame

3.2 振动筛机架刚度校核

对振动筛机架来说，刚度要求更为重要.对一般机架来说，建议挠度与长度的比值［3］，在垂直方向采用1/500～1/1 000，水平方向采用（柱受水平力的挠度比）1/1 000～1/2 000.振动筛机架在垂直方向的许用挠度有λY，表示机架往Y方向的变形量；振动筛机架在水平方向的许用挠度分别有λX，λZ，分别表机架往X和Z方向的变形量.振动筛机架的挠度与长度之比，在垂直方向取1/750，而在水平方向取1/1 500.振动筛机架许用挠度计算式为

λX=lX/（1 500nX），λY=lY/（750nY），λZ=lZ/（1 500nZ）.

式中：lY，lX和lZ分别为机架在垂直和水平方向上梁的有效长度，其值分别为1 285，1 320，2 370mm；nY，nX，nZ为安全系数，均取值1.5.因此，可得到许用挠度λY，λX，λZ分别为1.1，0.6，1.0mm.

优化后，振动筛机架在静力和周期性交变载荷下往X，Y和Z正、负方向最大位移，如表2所示.由表1可得出，振动筛机架在静力和周期性交变载荷下，往X，Y和Z正、负方向的总位移λ′tot：λ′tot，+X=0.121mm，λ′tot，-X=0.448mm，均小于λX；λ′tot，+Y=0.258mm，λ′tot，-Y=0.443mm，均小于λY；λ′tot，+Z=0.828mm，λ′tot，-Z=0.828mm，均小于λZ.由此可知，优化后的振动筛机架满足刚度要求.

表2 振动筛机架在静力和周期性交变载荷下的最大位移Tab.2 Maximum displacement in static and periodical changing load of vibrating screen frame mm

3.3 振动筛机架强度校核

振动筛机架强度校核采用古德曼（Goodman）图来评价［4］.振动筛机架材料强度极限σb为470.4MPa，疲劳极限σl为132.4MPa［5］，查设计手册，安全系数nl和nb分别取2.5和1.5，则σl/nl=53.0MPaσ，b/nb=313.6MPa.在校核时必须计算振动筛机架的静应力和动应力.优化后，振动筛机架静应力和动应力分布云图，如图4所示.

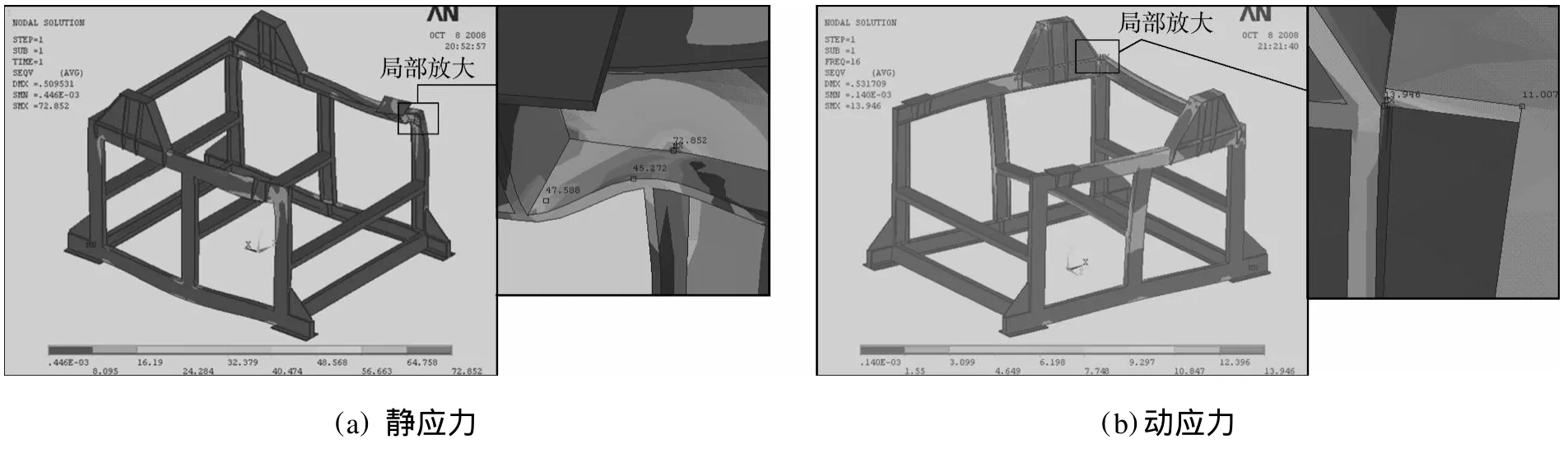
图4 振动筛机架应力分布云图Fig.4 Cloud diagram of stress distribution of vibrating screen frame

由图4可知，优化后振动筛机架的最大静应力和最大动应力，分别为72.9，14.0MPa.优化后振动筛机架的古德曼图，如图5所示.从图5可见，点（72.9，14.0）在古德曼图中处于“寿命线”（循环次数为107）下方，优化后振动筛机架满足强度要求.

图5 振动筛机架古德曼图Fig.5 Goodman diagram of vibrating screen frame

3.4 振动筛机架稳定性校核

对优化后振动筛机架提取前5阶屈曲载荷特征值［6-7］，分别为346.490，373.700，723.360，727.750，799.620kN.由此可知，优化后振动筛机架的最小屈曲载荷为346.490kN.振动筛机架所受的最大压力为36.040kN，机架的最小屈曲载荷是其所受最大压力的9.6倍，振动筛机架不会出现屈曲，即结构稳定性好.

4 结论

从振动筛机架的结构优化设计及对优化后振动筛机架的校核，可以得出以下4个结论.（1）优化设计后的振动筛机架，机架的总质量减小了29.41％，优化效果明显.（2）优化后的振动筛机架在满足刚度要求下，其强度一般可以满足设计要求.（3）优化后的振动筛机架不会出现失稳现象，结构稳定性好.（4）优化设计和结构校核结果，可为振动筛的标准化、大型化和系列化设计提供理论依据.

［1］刘惟信，孟嗣宗.机械最优化设计［M］.北京：清华大学出版社，1986：1-33.

［2］东方人华，祝磊，马赢.ANSYS 7.0入门与提高［M］.北京：清华大学出版社，2004：252-256.

［3］成大先.机械设计手册［M］.北京：化学工业出版社，2004：3-46.

［4］吕瑞典，许明.修正的古德曼应力图及许用安全系数［J］.石油学报，2001，22（6）：86-88.

［5］李舜酩.机械疲劳与可靠性分析［M］.北京：科学出版社，2006：230-234.

［6］张胜民.基于有限元软件ANSYS 7.0的结构分析［M］.北京：清华大学出版社，2003：177-222.

［7］陈铁云，沈惠中.结构的屈曲［M］.上海：上海科学技术文献出版社，1993.

Optimal Design of Vibrating Screen Frame

ZHAN G Ka-de，HUAN G Zhi-jian，HAO Yan-hua
（College of Mechanical Engineering and Automation，Huaqiao University，Quanzhou 362021，China）

The finite element model and optimal model of vibrating screen frame is built for its optimal design which has large reserve in rigidity，strength and stability.The rigidity，strength and stability of the vibrating screen frame is checked，with the dimension specification of design variables as the optimized value.The results have shown that the total weight of the vibrating screen frame after optimization is significantly reduced by 29.41％，and its rigidity and strength meets the design requirement.Moreover the optimized vibrating screen frame won’t occur the phenomenon of loss of stability and has a good structure stability.

vibrating screen frame；optimal design；strength；rigidity；stability

TD 452.02；TB 115

A

1000-5013（2010）04-0363-04

（责任编辑：陈志贤 英文审校：郑亚青）

2009-04-23

郝艳华（1956-），女，研究员，主要从事计算机辅助设计与工程的研究.E-mail：haoyh@hqu.edu.cn.

福建省科技重大专项基金资助项目（2006HZ02040038）