中低纬等离子体泡的非线性数值模拟

佘承莉 於 晓 罗伟华 冯 健 甄卫民

(1.中国电波传播研究所,山东 青岛266107;2.武汉大学电子信息学院,湖北 武汉430079)

1.引 言

电离层作为卫星信号传播的特殊媒介,对卫星通讯与导航定位等空间活动有着十分重要的意义。特别是由于电离层不规则体的存在,导致无线电波穿过电离层时发生闪烁,给依赖无线电波传播的空间活动带来严重影响,其影响从短波一直扩展到通信卫星和全球定位系统(GPS)的L波段和广播卫星的C波段[1]。电离层不规则体的空间尺度从几米到上千公里,持续的时间长度也因所处的纬度和季节等因素而有所不同。扩展F即是一种发生在电离层F区的不规则体,多见于赤道及低纬地区,主要包括等离子体泡、羽状不规则体和底部正弦型不规则体等多种形态[2-3]。基于测高仪、VHF雷达和卫星数据,我们可以得到等离子体泡的形态特征、上升过程及其空间分布[4]。

有关扩展F生成和发展的物理机制,已经有许多理论分析和数值模拟研究。一般认为,扩展F是由等离子体不稳定性造成的,日落以后,当F层底部存在一定幅度的密度扰动时,如果F层底部电子密度梯度足够大且F层峰值高度足够高,在赤道地区,R-T不稳定性[5]导致密度扰动不断增长,形成不规则体;在中纬地区,Perkins不稳定性[6]导致不规则体生成;随后,在E ×B模的作用下,不规则体向上抬升,形成泡状的等离子体耗尽区,即等离子体泡,最后到达并穿过F层峰值高度,等离子体泡基本上沿磁通量管的方向分布,同时向磁赤道两边延伸[4,7]。相关数值模拟工作主要在赤道-低纬地区展开[7-10],而中纬地区则相对较少[2,11-12],这些模拟结果与实验观测较为一致,可用于解释不规则体生成和发展的基本机制。但仍有一些观测结果不能用现有理论来解释[13],特别是中低纬地区所面临的问题则更加复杂,还有许多问题值得进一步研究。

此外,出于对电波传播应用的考虑,也有必要加强对中低纬地区不规则体生成机制的研究。我国长江以南的低纬地区,特别是台湾、福建、广东、广西、海南及南海地区,均处在磁赤道异常区的北驼峰附近,在全球范围内是电离层闪烁出现最频繁、影响最严重的地区之一[14]。

本文就中国中低纬地区展开数值模拟实验,研究不同纬度的等离子体不稳定性在不同背景电场条件下的演化过程,为将来我国开展天地基联合闪烁预报提供一定的理论支撑。

2.基本理论

采用直角坐标系,x轴指向西,y轴垂直地面向上,z轴指向北,地磁场B在y-z平面内(不考虑磁偏角)。描述电子和离子运动的基本方程可写作

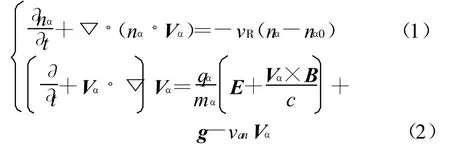
引入背景中性大气静止和电流准中性的假设,忽略电子的重力和碰撞,并且不考虑沿场向的传播和电离层F区沿磁力线的电位降落。采用扰动分析法,假设∂/∂z=0,E=E0+E1,下标 0代表稳态,1代表扰动,可由式(1)和式(2)得到稳态方程和扰动方程如下。

稳态方程

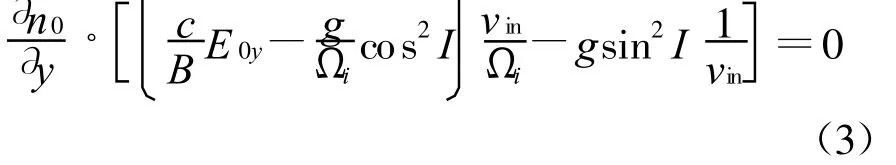
扰动方程

为了解本次强降水发生前大气中的水汽垂直分布和能量变化,以及高低层风场的配置情况,制作沿30.6°N的相对湿度RH、相当位温θe以及水平风场(u,v)的剖面(图3)。θe的垂直分布可以反映大气的对流性不稳定,当大气层中的θe随高度减小时,整层空气抬升后,大气层表现为整层位势的不稳定;反之,θe随高度增大时,整层空气抬升后,大气层能量将会变得更加稳定。

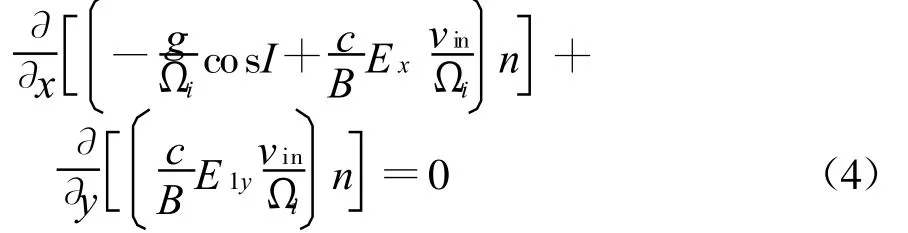
式中:I表示地磁倾角;Ωi表示离子的回旋频率。

考虑在以电子的零级漂移速度运动的参考坐标系中,电子的质量连续方程为

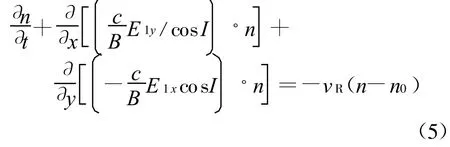
在静电假设条件下,E=-▽φ[5];φ是电动势,联立方程(4)、(5),得上述两式即为描述电子密度随时间变化的基本方程组。

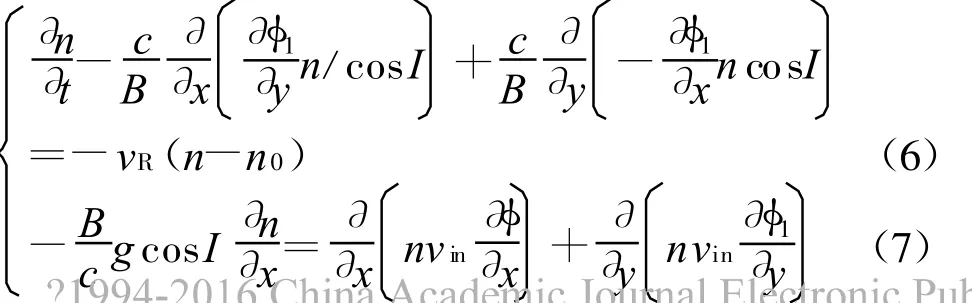
3.数值模拟结果

为了求解方程组(6)、(7)的非线性解,我们对其进行数值模拟。引入无量纲量Q=n/n0,方程组(6)、(7)变为

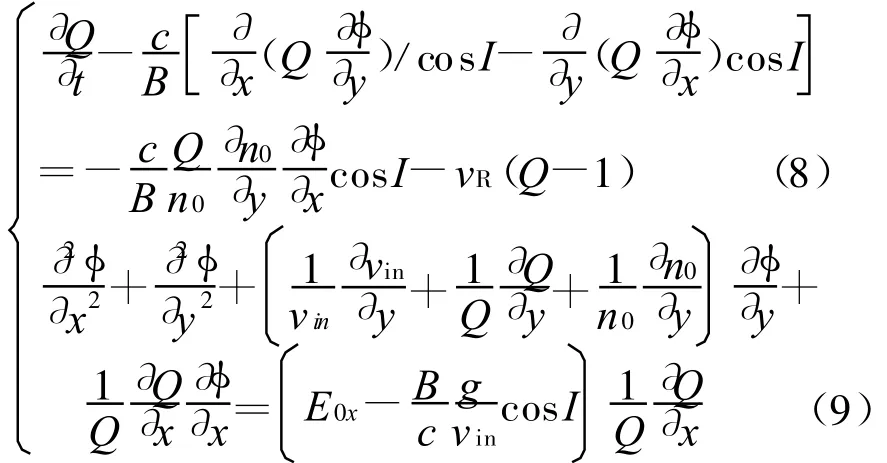
这就是数值模拟中用到的两个基本方程。

方程(8)采用通量传输修正(FCT)法[15-16]求解,方程(9)采用交替方向隐式法[16]求解。数值计算中采用二维正交均匀网格,水平和垂直方向网格间距均取为5 km。水平方向对Q和φ都采用周期边界条件,垂直方向则采用等值外推边界条件。方程(8)和(9)中的n0,v in和v R都是高度的函数,通过改变这些参量的值来仿真不同的电离层条件。背景电子密度 n0取自IRI-2007模型[17],如图 1;νin和νR取自文献[18],如图2。计算中取g=9.8 m/s2,B=0.3 G.

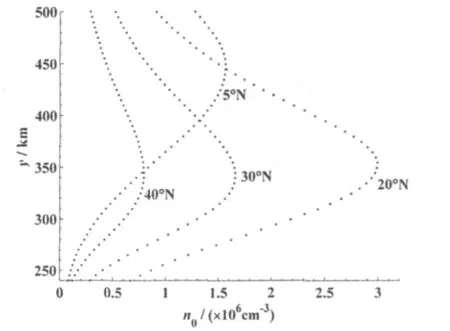
图1 不同地理纬度上的电子密度分布

初始扰动源来自密度的一维扰动

上述初始扰动的值在0.95和1.05之间,即初始扰动约为背景值的5%。

图2 νin和νR随高度的分布

本文选取在太阳活动高年(2002年)的春季(3月份),太阳月平均黑子数为110,110°E经线附近的磁赤道、海口、武汉和北京等4个地方,结合不同的初始背景电场水平进行了模拟。通过这组结果的比较,我们可以得到扩展F随纬度变化的特征及它在不同电场水平驱动下的表现。下面给出详细的模拟结果对比,LT表示模拟的初始时刻(地方时),t代表演化持续时间。

模拟1 磁赤道地区(地理坐标:5°N,110°E),I=0,=0,LT=19 h,模拟结果如图3所示。从图中可以看出,R-T模增长很快,在t=6000 s左右,等离子体泡可穿过F层峰,而且随着时间推移,Q值的幅度不断变大,在t=12000 s时,耗空区和密度增强区的Q值分别可达0.5和1.7,这是四个地区的模拟结果中不稳定性发展最快同时也是最强的。当E0x从0向-2 mV/m的水平变化时,不稳定性发展得越来越快,等离子体泡耗空的幅度也越强。作为比较,图4给出了E0x=-1 mV/m时不稳定性的演化过程。

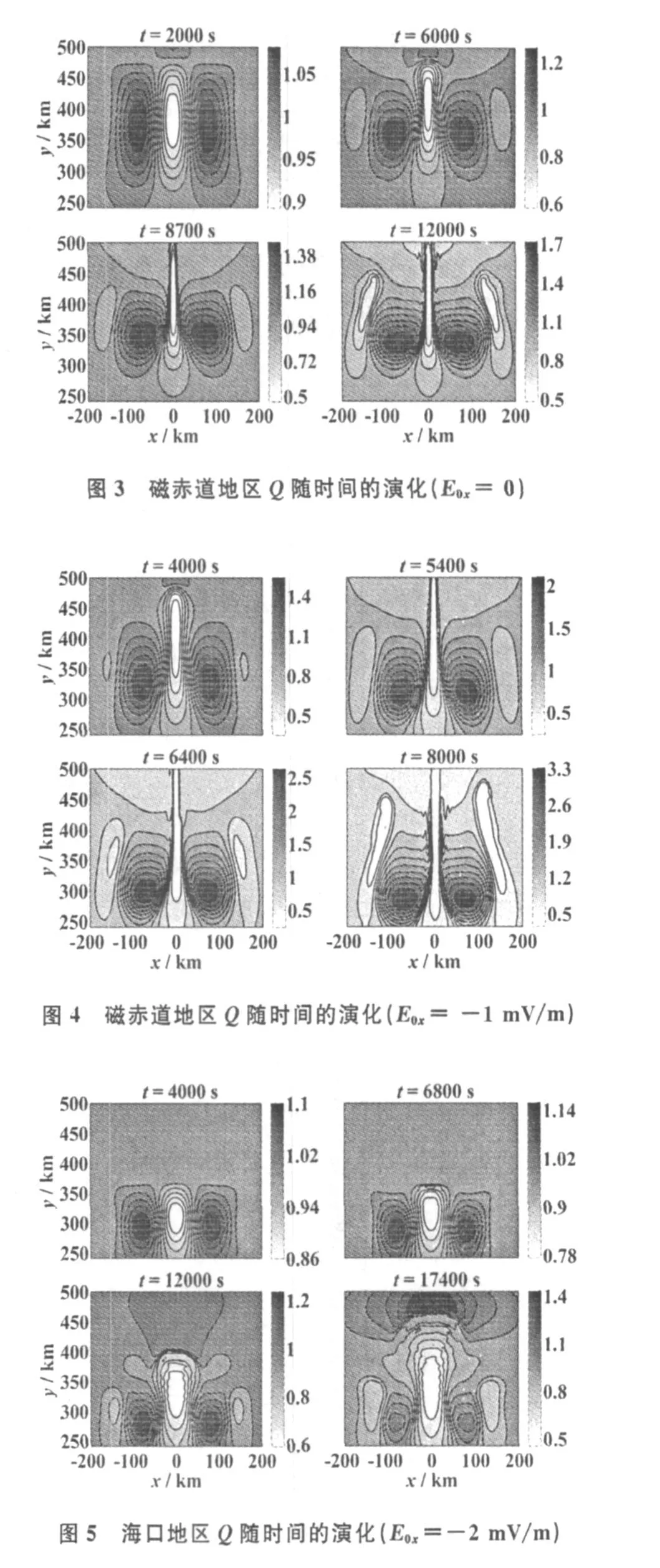
模拟2 海口地区(地理坐标:20°N,110°E),I=30°,LT=19 h。E0x=0时,扰动很快稳定下来;当E0x=-2 mV/m时,模拟结果如图5所示,在t=6800 s时等离子体耗空区的Q值可达0.78,在t=12000 s时等离子体泡到达F层峰值高度以上。

比较图3和图5,可以看出海口地区不稳定性发展的过程比磁赤道地区明显要慢,等离子体耗尽程度也相对弱一些;等离子体泡所能到达的高度也不同,磁赤道地区可达到500 km以上,而海口地区则到400 km左右,这可能是因为两者的背景电子密度分布显著不同,从图1可知,前者峰值高度为450 km,后者峰值高度为355 km,而且电子密度梯度的差别也很大,尤其是在峰值高度以下,海口地区的密度梯度比磁赤道地区大。

模拟3 武汉地区(地理坐标:30°N,114°E),I=40°,LT=21 h。E0x=0时,没有等离子体泡生成,不稳定性很快衰减下来。当E0x=-2 mV/m时,电子密度增强和耗空的幅度都不断增大,在t=8900 s时,Q的最小值已经达到0.75,此时一个较强的等离子体泡生成,在t=17400 s时等离子体泡穿过F层峰到达400 km的高度,模拟结果如图6所示。比较图5和图6,可以看到武汉地区的不稳定性发展过程与海口地区相当。

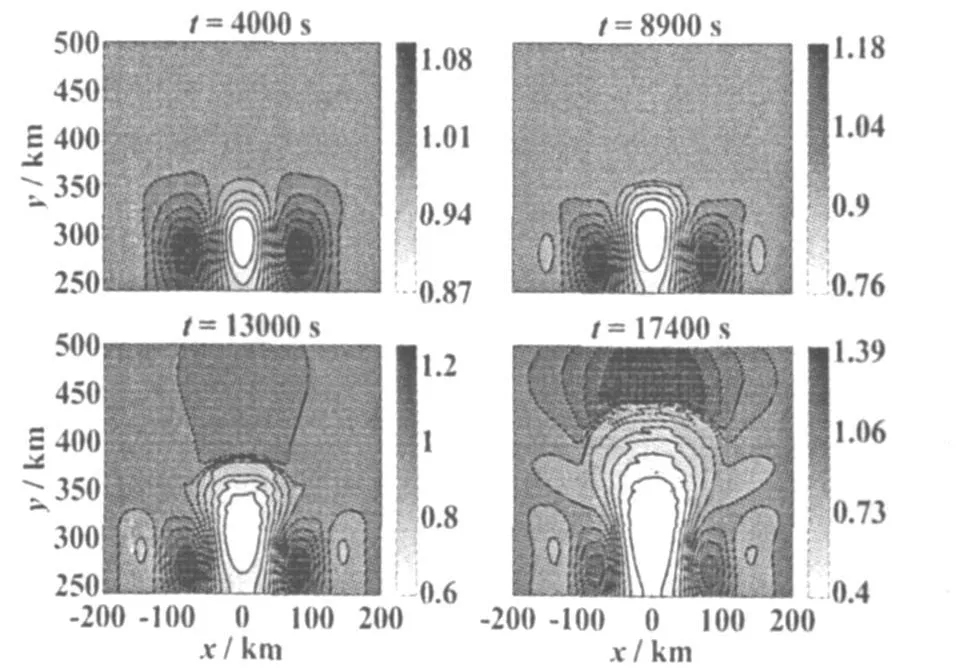
图6 武汉地区Q随时间的演化(E0x=-2 mV/m)

模拟4 北京地区(地理坐标:40°N,116°E),I=50°,LT=21 h。E0x=0时,模拟结果中看不到R-T模的增长,初始扰动很快稳定下来。当背景电场E0x=-2 mV/m时,相应的模拟结果如图7所示。

图7 中,在t=5000 s左右,底部有一个较弱的等离子体泡生成,同时还伴随等离子体密度加强区,当t=15000 s时,等离子体耗尽的幅度增大,直到t=20000s时耗空区Q值达到0.77。将图7与图5及图6对比可知,北京地区的不稳定性发展过程最慢,幅度也最弱,即使在t=20000 s时等离子体泡也无法上升到F层峰值高度(345 km)之上。

结果表明:在无背景电场作用的情况下,只有磁赤道地区有等离子体泡生成;当背景东向电场强度达-2 mV/m时,海口和武汉地区模拟的等离子体泡发展的程度相当,但相对磁赤道地区要弱,北京地区仅生成了很弱的等离子体泡,反映出北京地区对背景电场强度的依赖比海口和武汉地区更强。

4.讨论与结论

由上述模拟结果可以看出:对相同的密度扰动,在不同背景电场条件下,不同纬度地区的等离子体不稳定性发展过程不同。当E0x=0时,仅磁赤道地区的扰动能发展成等离子体泡,其它地区的扰动很快稳定下来;随着东向电场的增强,中低纬地区的不稳定性才逐渐发展起来。这可能是由于各个地区的背景电子密度分布不同导致的,通常认为,不稳定性的发展和背景电子密度梯度以及F层峰值高度有关,电子密度梯度和峰值高度越大,越有利于不稳定性的增长,本文中用到的磁赤道地区的峰值高度显著高于其它地区,而背景电子密度梯度也各不相同,相应地等离子体不稳定性的发展过程也差别很大,这也表明磁赤道地区扩展F出现规律可能有别于中低纬地区。在同一地区上空,不稳定性在不同背景电场条件下的演化过程也各不相同,随着东向电场分量的增强,不稳定性过程也发展得越迅速,程度越剧烈,这与已有文献的结论也是一致的[7]。

在磁赤道地区,不稳定性激发的等离子体泡较强,而且上升到F层峰值高度的速度也最快;而在海口地区(20°N)则需要在东向电场的作用下等离子体泡才能生成,这些等离子体泡最终也能到达F层峰值高度;武汉地区(30°N)的情形与海口地区相似;在北京地区(40°N)只能生成较弱的等离子体泡,并且泡很难上升到 F层峰值高度之上。文献[11]选择与本文不同的季节和扰动的空间尺度,海口地区的纯R-T模便可以生成较强的等离子体泡。这也可能是由于季节不同导致各自的背景电子密度分布尤其是峰值高度与电子密度梯度不同引起的。

本文引入的电场模型仅为水平分布的东向电场,忽略了它在垂直方向的梯度,与实际电场的分布还存在差别,因此,进一步将合理的电场模型引入到现有的非线性模型中具有重要意义。潮汐风场、赤道电集流以及跨赤道的中性风场[19-22]对电离层中的电场都有重要的影响,如何将这些因素都引入到现有的模型中,将是下一步工作的重点。

除了本文所提及的背景电子密度梯度、峰值高度、背景电场、重力、地磁场和碰撞等因素,热层风场以及沿通量管积分的Pedersen电导率等物理量也能影响不稳定性的发展[22],如何将这些因素都同化进一个模型中,构建一个实用的闪烁监测和预报系统,如美国的C/NOFS计划[23],将在后续工作中进一步研究。

[1] STEENBURGH RA,SMITHTRO CG,GROVESK M.Ionospheric scintillation effects on single frequency GPS[J].Space Weather,2008,6,S04D02,doi:10.1029/2007SW000340.

[2] 谢 红.中低纬Spread-F的数值模拟及BSS现象的讨论[D].北京大学,1991.

[3] ABDU M A.Outstanding problems in the equatorial ionosphere-thermosphere electrodynamics relevant to spread F[J].J.Atmos.Solar Terr.Phys.,2001,63(9):869-884.

[4] HYSELL D L.An overview and synthesis of plasma irregularities in equatorial spread F[J].J.Atmos.Solar Terr.Phys.,2000,62:1037-1056.

[5] KELLEY M C.The Earth's Ionosphere:Plasma Physics&Electrodynamics[M].San Diego,Academic Press Inc.,1989.

[6] PERKINS F.Spread F and ionospheric currents[J].J.Geophys.Res.,1973,78(1):218-226.

[7] 罗伟华,徐继生,徐良.赤道电离层R-T不稳定性发展的控制因素分析[J].地球物理学报,2009,52(4):849-858.

LUO Weihua,XU Jisheng,XU Liang.Analysis of controlling factors leading to the development of R-T instability in equatorial ionosphere[J].Chinese J.Geophys.,2009,52(4):849-858.(in Chinese)

[8] SEKAR R.Plasma instabilities and their simulations in the equatorial F region:recent results[J].Space Sci.Rev.,2003,107(1-2):251-262.

[9] HUBA JD,JOYCE G,KRALL J.Three-dimensional equatorial spread F modeling[J].Geophys.Res.Lett.,2008,35,L10102,doi:10.1029/2008GL033 509.

[10] K RA LL J,HUBA J D,JOYCE G,et al.Three-dimensional simulation of equatorial spread-F with meridional wind effects[J].Ann.Geophys.,2009,27:1821-1830.

[11] 谢 红,肖 佐.中低纬Spread-F的数值模拟[J].地球物理学报,1993,36(1):18-26.

XIE Hong,XIAO Zuo.Numerical simulation of spread-F in low and mid-latitudes[J].Acta Geophysica Sinica,1993,36(1):18-26.(in Chinese)

[12] 黄朝松,KELLEY M C.中纬电离层大尺度扰动的数值模拟[J].地球物理学报,1997,40(3):301-310.

HUANG Chaosong,KELLEY M C.Numerical simulations of large scale perturbations in the midlatitude F region[J].Acta Geophysica Sinica,1997,40(3):301-310.(in Chinese)

[13] WOODMAN RF.Spread-F an old equatorial aeronomy problem finally resolved[J].Ann.Geophys.,2009,27:1915-1934.

[14] 甄卫民,陈丽.中国电离层闪烁监测和预报[J].电波科学学报,2004,19(Sup.):207-208.

[15] ZALESAK ST.Fully multidimensional fluxcorrected transport algorithms for fluids[J].J.Comput.Phys.,1979,31:335-362.

[16] 傅竹风,胡友秋.空间等离子体数值模拟[M].合肥:安徽科学技术出版社,1995.

[17] BILITZA D,REINISCH B.International reference ionosphere 2007:improvements and new parameters[J].Adv.Space Res.,2008,42(4):599-609.

[18] STROBEL D F,MCELROY M B.The F2-layer at mid-latitudes[J].Planet Space Sci.,1970,18:1181-1202.

[19] FARLEY D T,BONELLI E,FEJER B G,et al.The prereversal enhancement of the zonal electric field in the equatorial ionosphere[J].J.Geophys.Res.,1986,91(A12):13,723-13,728.

[20] HAERENDEL G,ECCLES J V.The role of the equatorial electrojet in the evening ionosphere[J].J.Geophys.Res.,1992,97(A 2),1181-1192.

[21] M ENDILLO M,BAUMGARDNER J,PI X,et al.Onset conditions for equatorial spread F[J].J.Geophys.Res.,1992,97(A9),13,865-13,876.

[22] SULTAN P J.Linear theory and modeling of the Rayleigh-Taylor instability leading to the occurrence of equatorial spread F[J].J.Geophys.Res.,1996,101(A12):26,875-26,891.

[23] de La BEAUJARDIÈRE O,JEONG L,BASU B,et al.C/NOFS:a mission to forecast scintillations[J].J.Atmos.Solar Terr.Phys.,2004,66:1573-1591.