大跨斜拉桥多维多点地震反应特性研究

全 伟

0 引言

大跨斜拉桥是目前大跨径桥梁中经常采用的一种桥型,深入了解其在多维多点地震激励下的响应特征对于桥梁的抗震设计具有重要的指导意义。项海帆[1]对天津永和桥的研究表明,行波效应对漂浮体系斜拉桥是有利的;而陈幼平等[2]同样对该桥进行了行波效应的影响分析,研究结果则不一样,在三向正交分量作用下,行波效应可能使得斜拉桥的地震响应显著增加,塔根弯矩和主梁轴力都可能有较大程度的增长;史志利等[3]对香港昂船洲大桥进行了多点激励下的地震响应分析,认为多点激励下斜拉桥地震响应分析与具体的跨径布置、质量和刚度分布以及节点连接方式等多种因素有关。

本文研究了相同和不同支承点的不同分量之间的相干性对桥梁的影响,并提出了简化的考虑多维多点地震反应的方法,可供大跨斜拉桥抗震设计时参考。

1 多维多点反应谱方法

目前各国研究者基于各个台阵记录提出的相干函数模型很多。本文研究时采用Luco和Wong[4]提出的相干函数考虑地震动的空间变化效应:

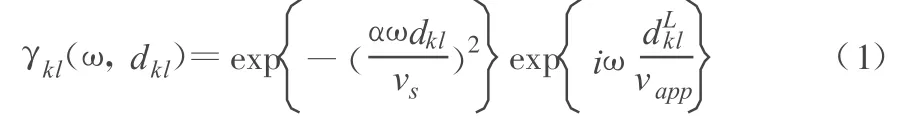
其中,α为相干系数;vs为土层剪切波速;vapp为地震地面运动的视波速;dkl为地面k点和l点之间的距离;dLkl为两点距离沿着结构主轴的投影长度。相干系数α是地面运动的相干损失随着距离和频率的变化的一种度量。α和vs的比值由下式确定:

Luco和Wong根据几次台阵的观察结果,认为对于中等的相干性,q的取值范围为:2≤q≤3。当 α/vs的值趋近于 0时,公式(1)中的第一项趋近于1,相干函数仅仅反映行波效应的影响。当vapp趋近于无穷大时,公式(1)中的第二项趋近于1,相干函数仅仅反映部分相干效应的影响。

2 斜拉桥算例

以某双塔双索面连续主梁漂浮体系斜拉桥为例进行分析,跨径布置(134+274+134)m,主塔为H形,主索为半竖琴形,主梁为钢—混结合梁。本文采用简化的集中质量有限元模型,见图1。

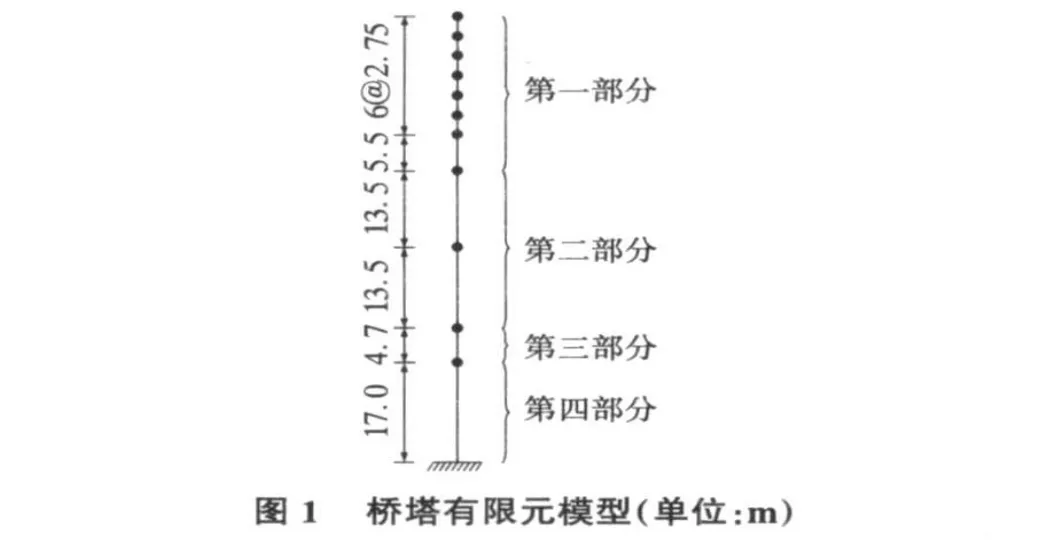
3 数值结果

研究时,假定各点同一分量的相干函数相同,均采用Luco-Wong模型,其中部分相干效应取中等程度的相干值(α/vs=2.5×10-4),行波波速取250 m/s。不同点水平地震动分量和竖向地震动分量的相干系数假定与频率无关,取为0,0.2,0.6,1四种等级,不同点不同地震动分量之间的行波效应因子同不同点相同分量的考虑方法。另外,在考虑不同点不同分量相干性时,同时考虑了同一点不同分量之间的相干性,同样假设其值相应的为0,0.2,0.6,1四种等级。

图2给出了各种不同相干程度下桥面板竖向位移的变化曲线。图中0.2+0.2指的是同时考虑同一点不同分量之间的相干性(相干系数为0.2),以及不同点不同分量之间的相干性(相干系数为0.2,行波效应因子同不同点相同分量的考虑方法)。其余图例的含义可类推。从图上可以看出,随着不同点不同地震动分量相干系数增加,竖向位移呈增加的趋势。只考虑同一点不同分量之间的相干性,相干系数为0.2,0.6和1.0时比相干系数为0分别高4.4%,12.8%和20.5%,而同时考虑同一点和不同点不同分量之间的相干性,两者相干系数均为0.2,0.6和1.0时比相干系数为0则分别高出6.6%,18.7%和29.6%。可见,不考虑不同点不同分量之间的相干性同样可能低估桥梁结构的响应。

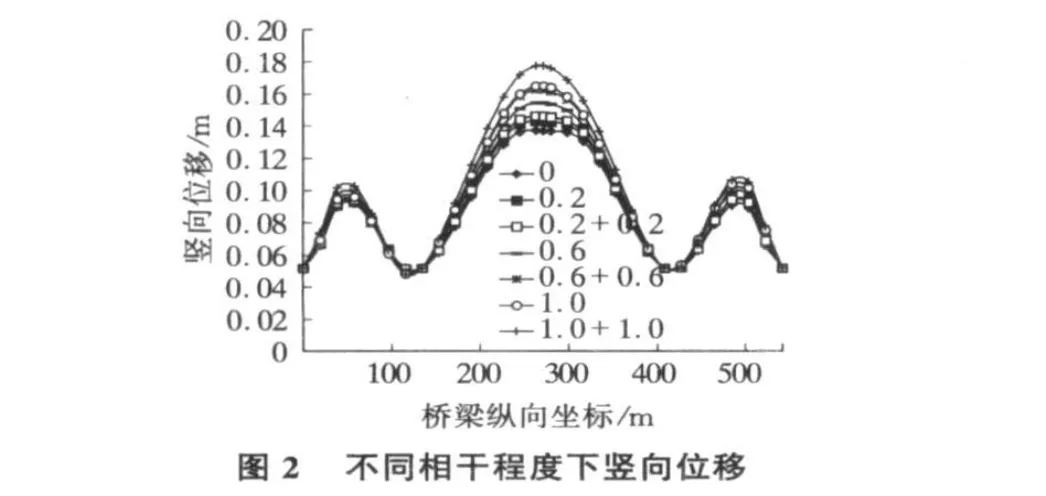
图3给出了各种不同相干程度下桥面板各节点纵向位移的变化曲线。可以看出,同时考虑不同点和相同点不同地震动分量之间的相干性,与只考虑相同点不同地震动分量相干性,对于纵向位移,两者幅值相差很小,可忽略。

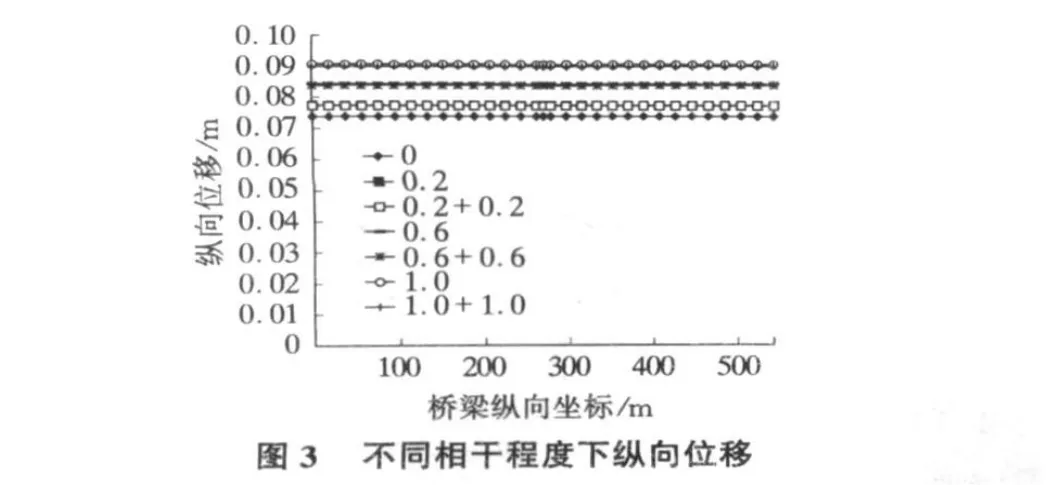
由塔顶纵向位移在各个工况下的计算结果可以看出,同时考虑同一点和不同点不同分量之间的相干性与只考虑同一点不同分量之间的相干性,塔顶的纵向位移值基本相同,可见,是否考虑不同点不同分量之间的相干性对桥塔纵向位移的值影响很小,可以忽略。综合桥面板和桥塔的位移反应的结果,地震动不同点不同分量之间的相干性对主梁竖向位移影响较大,而对主梁纵向位移和主塔纵向位移影响很小,基本可以忽略。

表1给出了中跨跨中和桥塔塔底内力的具体值。

表1 不同相干程度下桥梁内力响应

由表1可以看出:1)对于桥面板弯矩,相应于只考虑同一点不同分量之间的相干性,同时考虑同一点和不同点地震动不同分量之间的相干性可使弯矩有一定程度的增加,如表1中跨中弯矩的值1.0+1.0工况比相干系数为零的工况增加24%,而1.0工况只增加13%。对于桥面板剪力和轴力在中跨跨中部位,同时考虑不同点和相同点不同分量相干性相应于只考虑同一点不同分量相干性基本无影响或略有下降。但是在其他区域,如桥梁两端处剪力和塔根处轴力均有一定程度的增加。2)对于桥塔的受力,相应于只考虑同一点不同分量之间的相干性,同时考虑同一点和不同点地震动不同分量之间的相干性均相差不大,其中,桥塔弯矩略有下降,而剪力和轴力均有所增加。

4 结语

1)对于大跨斜拉桥,纵向激励和竖向激励耦合,而横向激励与纵向、竖向激励基本不耦合。同时考虑纵向和竖向地震动分量进行多维多点地震反应分析时,研究表明同一点不同分量之间的相干性和不同点不同分量之间的相干性都可能使得结构的地震响应增大。同一点不同分量之间的相干性和不同点不同分量之间的相干性的取值区间偏不利取[0,0.6],可以知道考虑这两种相干性后,对于结构位移放大系数在15%左右,内力放大系数在10%左右。2)多维多点简化为单维多点地震反应分析。其中,纵向和竖向地震动分量由于是相互耦合的,利用SRSS法组合法进行组合,另外考虑到同一点地震动不同分量和不同点不同地震动分量相干性影响,可对结构的地震响应乘以一个放大系数 γ,近似的考虑两种相干性对桥梁的影响。横向地震动则单独进行计算。其中,Rz为纵向地震动作用下结构的响应;Rs为竖向地震动作用下结构的响应;Rh为横向地震动作用下结构的响应;R1和 R2分别为纵、竖向地震动同时作用以及横向地震动单独作用时对应的反应量;γ的取值参考本文桥梁,对于位移值取1.15,内力值可取1.1。

[1]项海帆.斜张桥在行波作用下的地震反应分析[J].同济大学学报,1983,11(2):1-9.

[2]陈幼平,周宏业.斜拉桥地震反应的行波效应[J].土木工程学报,1996,29(6):61-68.

[3]史志利,李忠献,陈 平.大跨度斜拉桥多点激励地震反应分析[J].特种结构,2004,21(2):46-50.

[4]Luco J.E.,Wong H.L..Response of a rigid foundation to a spatially random ground motion[J].Earthquake Engineering and Structural Dynamics,1986(14):891-908.