型钢混凝土—钢筋混凝土结构地震反应时程分析
沈古成 司旭涛 苏艳梅
0 引言
《型钢混凝土组合结构技术规程》中,将型钢混凝土组合结构(Steel Reinforced Concrete Composite Structure)定义为混凝土内配置轧制型钢或焊接型钢和钢筋的结构,简称SRC结构。结合我国的国情,考虑到工程造价、施工工艺、施工周期等各个因素的影响,在结构中完全采用型钢混凝土结构是不现实的,而只能在一些结构的关键部位使用。本文所要研究的型钢混凝土—钢筋混凝土组合结构是在SRC结构的基础之上,在我国有广泛的应用前景。
时程分析法[1]通过逐步积分进行结构弹塑性动力分析,可以计算出地震反应全过程中各个时刻的内力和变形状态,确定结构开裂和屈服的时刻和顺序,发现应力和塑性变形集中的部位,从而判明结构的屈服机制、薄弱环节及可能的破坏类型。
1 动力方程
在对结构进行弹塑性反应分析时,因为刚度矩阵随着时间而变化,振型频率也随时间而变化,因而振型分解法不宜在此使用,只能应用逐步积分法的直接动力法。要准确地研究结构或构件的弹塑性动力反应,需要解决的问题有很多,主要包括:地面运动、结构或构件的恢复力模型,计算模型的选取,动力方程的数值解法等。
一般多自由度体系的动力方程为:
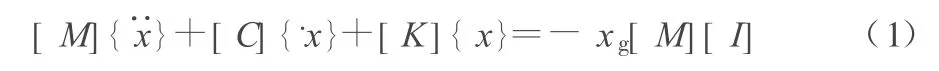
其中,[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;xg为地面加速度;[I]为时间 t的函数;{},{x},{x}分别为结构的加速度、速度和位移反应列阵,均为时间t的函数。
当地面运动已知时,通过动力方程式(1)求解{x},{x},{x}采用逐步积分法。
多自由度体系在多维空间体系下的动力方程为:
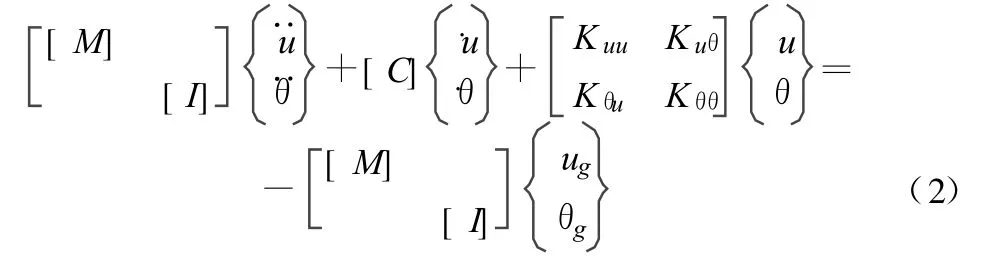
其中,[I]为截面惯性模量;{u},{u},{u},{θ},{θ},{θ}分别为结构平动的加速度、速度和位移反应列阵与转动的加速度、速度和位移反应列阵[2]。
要将上式得出结果,需要确定结构的力学模型、恢复力模型、阻尼比和地震波等条件,还需一个良好的数值积分方法。
2 算例模型
本例中的计算模型为9层型钢混凝土—钢筋混凝土组合结构框架,首层层高3.6 m,其他层层高3 m,总高度是27.6 m,结构平面图如图1所示,结构立体图如图2所示,场地类别为Ⅱ类,场地土特征周期为0.45 s,抗震设防烈度为7度,属丙类建筑,抗震等级为三级,设地震分组为第一组,设计基本加速度值为0.1g。采用全框架结构体系,楼面采用150 mm厚混凝土板,板采用壳单元模拟,框架梁的尺寸为500 mm×250 mm,框架柱的尺寸及柱中型钢尺寸如表1所示,梁、柱采用HRB335级钢筋,柱的混凝土强度等级C30,梁的混凝土强度等级C20,楼面恒载取4.0 kN/m2,活载取2.0 kN/m2;屋面恒载取4.5 kN/m2,活载取0.5 kN/m2[3,4]。文中的方案一为纯框架结构,方案二、方案三为型钢混凝土与普通钢筋混凝土的组合结构。

按照抗震规范,地震波选用EL-Centro波,其记录峰值加速度为341.7 gal,卓越周期为0.55 s,时间步长为0.02 s,持续时间为30 s,按照7度基本烈度加速度时程曲线最大值要求,将地震波的峰值加速度放大值100 gal,在ETABS中输入放大系数1 000/341.7=2.926 5。在基本烈度下的非线性弹塑性时程分析时,根据抗震规范,框架结构在多遇地震下的阻尼比,对超过 12层的可采用0.02;在罕遇地震下的分析,阻尼比可采用0.05。
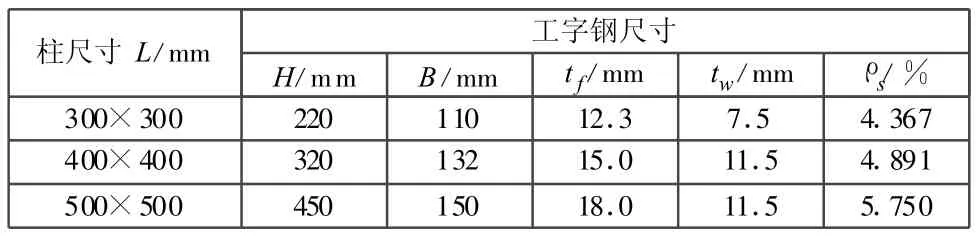
表1 型钢尺寸表
3 计算结果
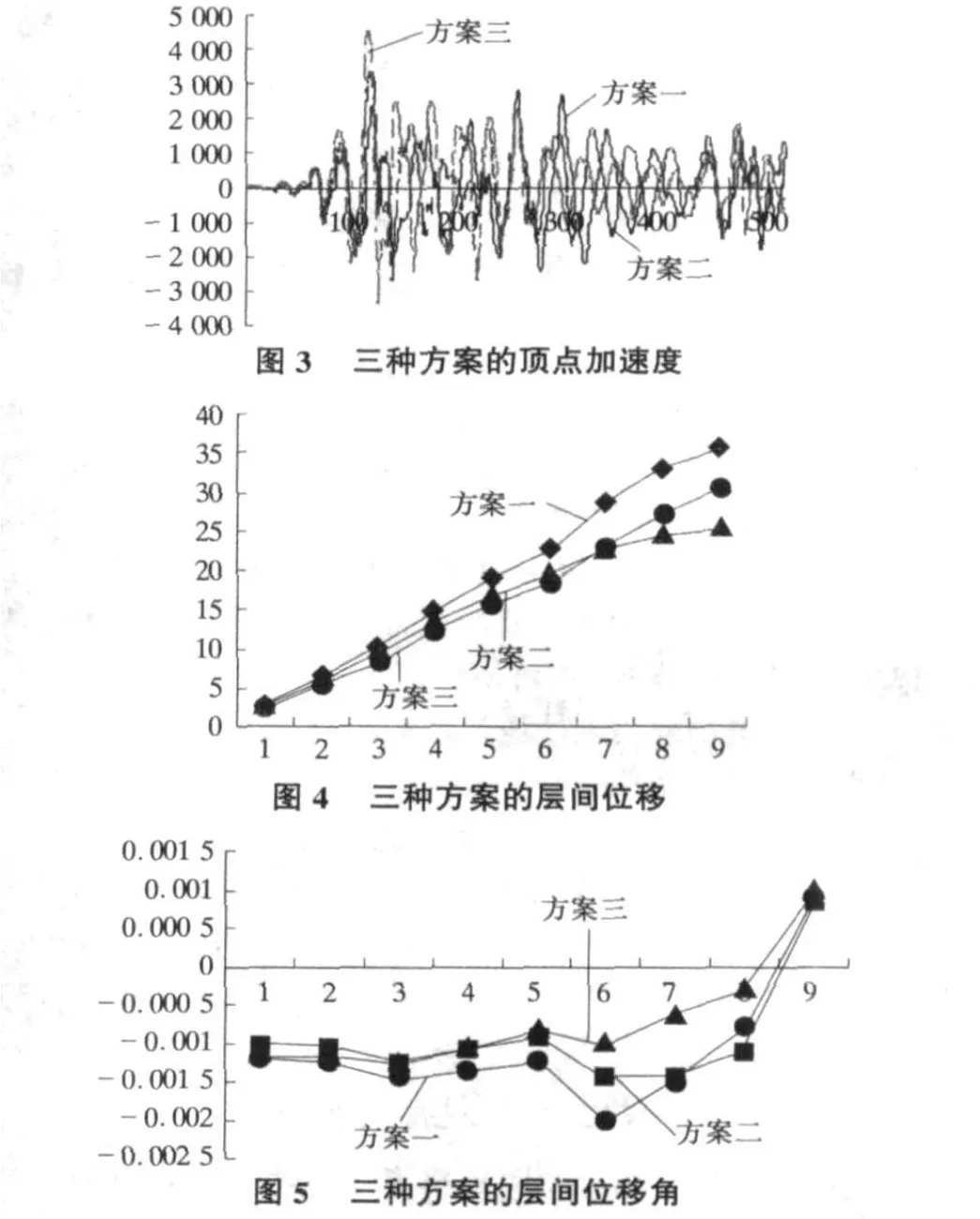
各种结构的顶点加速度、层间位移及层间位移角分别如图3~图5所示。
4 结语
从三种方案的顶点加速度曲线可以看出,型钢混凝土的消能减震效果明显;当然它们的层间位移角都小于1/50,符合规范要求。在EL-Centro波作用下,型钢混凝土组合结构的最大位移比纯框架结构的要小,其耗能性能比混凝土框架结构要好,故而应该推广使用型钢混凝土组合结构。
[1]蒋丽忠,王 臣.型钢混凝土—钢筋混凝土组合框架结构的地震弹塑性时程分析[J].铁道科学与工程学报,2008,5(2):18-24.
[2]包世华,方鄂华.高层建筑结构设计[M].第 2版.北京:清华大学出版社,2000.
[3]GB 50009-2001,建筑结构荷载规范[S].
[4]陈基发,沙志国.建筑结构荷载设计手册(第二册)[M].北京:中国建筑工业出版社,2004.
[5]吕西林.高层建筑结构[M].武汉:武汉工业大学出版社,2000.
[6]齐 欣.型钢混凝土—钢筋混凝土混合框架抗震性能分析[D].成都:西南交通大学,2003.
[7]JGJ 138-2001,型钢混凝土组合结构技术规程[S].

